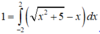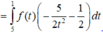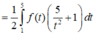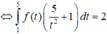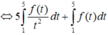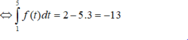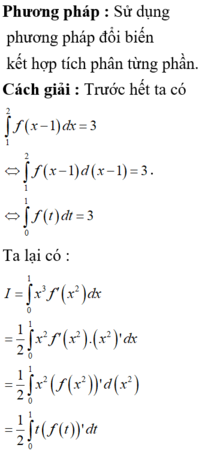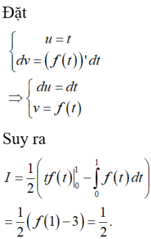Giải tích phân sau (X2 +1) e2x dx
PT
Những câu hỏi liên quan
Phương trình
e
x
-
e
2
x
-
1
1
-
x
2
+
2
2
x
+
1
có nghiệm trong khoảng nào sau đây? A.
1
2
;
1
B.
2
;...
Đọc tiếp
Phương trình e x - e 2 x - 1 = 1 - x 2 + 2 2 x + 1 có nghiệm trong khoảng nào sau đây?
A. 1 2 ; 1
B. 2 ; 5 2
C. 1 ; 3 2
D. 3 2 ; 2
Đáp án B
Phương pháp:
Sử dụng tính đơn điệu của hàm số.
Cách giải:
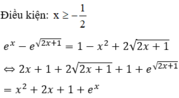
![]()
![]()

Đúng 0
Bình luận (0)
Xét sự hội tụ tích phân suy rộng loại 2:
1
ʃ ( lnx/1-x2) dx
0
Cho hàm số f(x) liên tục trên R và thỏa mãn
∫
-
2
2
f
(
x
2
+
5
-
x
)
d
x
1
,
∫
1
5
f
(
x
)
x...
Đọc tiếp
Cho hàm số f(x) liên tục trên R và thỏa mãn ∫ - 2 2 f ( x 2 + 5 - x ) d x = 1 , ∫ 1 5 f ( x ) x 2 d x = 3 Tích phân
∫ 1 5 f ( x ) d x bằng
A. -15
B. -2
C. -13
D. 0
Cho hàm số yf(x) có đạo hàm liên tục trên [0;1] thỏa mãn và
∫
1
2
f
(
x
-
1
)
d
x
3
và f(1)4. Tích phân
∫
0
1
x
3
f
(
x
2
)
d...
Đọc tiếp
Cho hàm số y=f(x) có đạo hàm liên tục trên [0;1] thỏa mãn và ∫ 1 2 f ( x - 1 ) d x = 3 và f(1)=4. Tích phân ∫ 0 1 x 3 f ' ( x 2 ) d x bằng
![]()
![]()
Tích phân ∫ 0 1 x ( x 2 + 3 ) d x bằng:
A. 2
B. 1
C. 4/7
D. 7/4
Cho hàm số f(x) liên tục trên R và các tích phân
∫
0
π
4
f
(
tan
x
)
d
x
4 và
∫
0
1
x
2
f
(
x
)
x
2...
Đọc tiếp
Cho hàm số f(x) liên tục trên R và các tích phân ∫ 0 π 4 f ( tan x ) d x = 4 và ∫ 0 1 x 2 f ( x ) x 2 + 1 d x , tính tích phân I = ∫ 0 1 f ( x ) d x
A. 6
B. 2
C. 3
D. 1
Chọn A.
Đặt t = tan x => dt = (1+ tan x) dx => d t 1 + t 2 = d x
Đổi cận x = 0=> t = 0 và x = π 4 = > t = 1
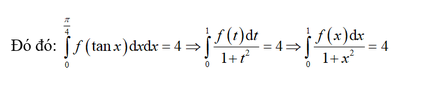
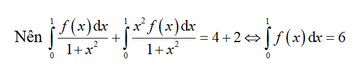
Đúng 0
Bình luận (0)
Biết
∫
1
4
f
(
x
)
6
và
∫
4
5
f
(
x
)
d
x
10
, khi đó
∫
1
2
f
(
4
x
-
3
)
d
x
-
∫
0...
Đọc tiếp
Biết ∫ 1 4 f ( x ) = 6 và ∫ 4 5 f ( x ) d x = 10 , khi đó ∫ 1 2 f ( 4 x - 3 ) d x - ∫ 0 ln 2 f ( e 2 x ) e 2 x d x bằng
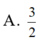

![]()
![]()
Cho hàm số f(x) liên tục trên
ℝ
thỏa mãn
∫
0
99
f
(
x
)
d
x
2
. Khi đó tích phân
I
∫
0
e
99
-
1
x
x
2
+...
Đọc tiếp
Cho hàm số f(x) liên tục trên ℝ thỏa mãn ∫ 0 99 f ( x ) d x = 2 . Khi đó tích phân I = ∫ 0 e 99 - 1 x x 2 + 1 f ( ln ( x 2 + 1 ) ) d x bằng bao nhiêu?
A. 1.
B. 2.
C. 3.
D. 4.
Giá trị tích phân
I
∫
0
1
(
x
3
+
6
x
)
2017
(
x
2
+
2
)
d
x
A.
7
2018
3
....
Đọc tiếp
Giá trị tích phân I = ∫ 0 1 ( x 3 + 6 x ) 2017 ( x 2 + 2 ) d x
A. 7 2018 3 . 2017
B. 7 2018 3 . 2018
C. 7 2018 2018
D. 7 2017 3 . 2017