Các câu hỏi tương tự
Cho f(x)
x
x
2
+
1
(
2
x
2
+
1
+
2017
)
, biết F(x) là một nguyên hàm của f(x) thỏa mãn F(0)2018. Tính F(2) A. F(2) 5+2017
5
B. F(2) 4+2017
4
C. F(2) 3+2017
3...
Đọc tiếp
Cho f(x)= x x 2 + 1 ( 2 x 2 + 1 + 2017 ) , biết F(x) là một nguyên hàm của f(x) thỏa mãn F(0)=2018. Tính F(2)
A. F(2) = 5+2017 5
B. F(2) = 4+2017 4
C. F(2) = 3+2017 3
D. F(2)= 2022
Số giá trị nguyên dương của m để hàm số
y
1
3
x
3
-
3
x
2
+
(
m
-
2017
)
x
+
2018...
Đọc tiếp
Số giá trị nguyên dương của m để hàm số y = 1 3 x 3 - 3 x 2 + ( m - 2017 ) x + 2018 nghịch biến trên khoảng (0;2) là
A. 2015.
B. 2017.
C. 2016.
C. 2016.
Giá trị của
A
1
1
!
.2018
!
+
1
2
!
.2017
!
+
1
3
!
.2016
!
+
...
+...
Đọc tiếp
Giá trị của
A = 1 1 ! .2018 ! + 1 2 ! .2017 ! + 1 3 ! .2016 ! + ... + 1 1008 ! .1011 ! + 1 1009 ! .1010 ! bằng
A. 2 2017 − 1 2018 ! .
B. 2 2017 2018 ! .
C. 2 2017 2019 ! .
D. 2 2018 − 1 2019 ! .
Cho hàm số
f
(
x
)
a
x
3
+
b
x
2
+
c
x
+
d
,
(
a
,
b
,
c
,
d
∈
ℝ
)
thỏa mãn
a
0
,
d
0
2018
,
a
+...
Đọc tiếp
Cho hàm số f ( x ) = a x 3 + b x 2 + c x + d , ( a , b , c , d ∈ ℝ ) thỏa mãn a > 0 , d > 0 > 2018 , a + b + c + d - 2018 < 0 Tìm số điểm cực trị của hàm số y = f ( x ) - 2018
A. 2
B. 1
C. 3
D. 5
Cho hàm số
y
f
x
có đạo hàm cấp hai trên R. Biết
f
0
3
;
f
2
-
2018
và bảng xét dấu của
f
0
như sau:Hàm số
y
f
x
+
2017...
Đọc tiếp
Cho hàm số y = f x có đạo hàm cấp hai trên R. Biết f ' 0 = 3 ; f ' 2 = - 2018 và bảng xét dấu của f ' ' 0 như sau:
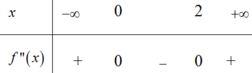
Hàm số y = f x + 2017 + 2018 x đạt giá trị nhỏ nhất tại điểm x 0 thuộc khoảng nào sau đây?
A. 0 ; 2
B. - ∞ ; - 2017
C. - 2017 ; 0
D. 2017 ; + ∞
Cho biểu thức
f
x
1
2018
x
+
2018
.
Tính tổng sau
S
2018
[
f
−
2017
+
f
−
2016
+
...
+
f...
Đọc tiếp
Cho biểu thức f x = 1 2018 x + 2018 . Tính tổng sau
S = 2018 [ f − 2017 + f − 2016 + ... + f 0 + f 1 + ... + f 2018 ]
A. S = 2018
B. S = 1 2018
C. S = 2018
D. S = 1 2018
Cho hàm số
f
(
x
)
a
x
3
+
b
x
2
+
c
x
+
d
với
a
,
b
,
c
,
d
∈
ℝ
,
a
0
và
d
2018
a
+
b
+...
Đọc tiếp
Cho hàm số f ( x ) = a x 3 + b x 2 + c x + d với a , b , c , d ∈ ℝ , a > 0 và d > 2018 a + b + c + d - 2018 < 0 . Số cực trị của hàm số y = f ( x ) - 2018 bằng
A. 3
B. 2
C. 1
D. 5
Cho hàm số
f
x
xác định trên
R
1
thỏa mãn
f
x
1
x
-
1
,
f
0
2017
,
f
2
2018
.Tính
S...
Đọc tiếp
Cho hàm số f x xác định trên R \ 1 thỏa mãn f ' x = 1 x - 1 , f 0 = 2017 , f 2 = 2018 .Tính S = f 3 - 2018 f - 1 - 2017
A. S = 1
B. S = 1 + ln 2 2
C. S = 2ln2
D. S = ln 2 2
Trong không gian Oxyz, cho 2 mặt phẳng (P): x + 2y – 2z +2018 0, (Q): x + my + (m – 1)z + 2017 0 (m là tham số thực). Khi hai mặt phẳng (P) và (Q) tạo với nhau một góc nhỏ nhất thì điểm M nào dưới đây nằm trong (Q) ? A. M(–2017;1;1) B. M(0;0;2017) C. M(0;–2017;0) D. M(2017;1;1)
Đọc tiếp
Trong không gian Oxyz, cho 2 mặt phẳng (P): x + 2y – 2z +2018 = 0, (Q): x + my + (m – 1)z + 2017 = 0 (m là tham số thực). Khi hai mặt phẳng (P) và (Q) tạo với nhau một góc nhỏ nhất thì điểm M nào dưới đây nằm trong (Q) ?
A. M(–2017;1;1)
B. M(0;0;2017)
C. M(0;–2017;0)
D. M(2017;1;1)
Giá trị của tích phân
∫
0
2018
x
(
x
-
1
)
(
x
-
2
)
.
.
.
(
x
-
2018
)
d
x
bằng A. 0 B. 1 C. 2017 D. 2018
Đọc tiếp
Giá trị của tích phân ∫ 0 2018 x ( x - 1 ) ( x - 2 ) . . . ( x - 2018 ) d x bằng
A. 0
B. 1
C. 2017
D. 2018



