Giúp mình giải nhanh với được không ạ...
H24
Những câu hỏi liên quan
giải nhanh giúp mình với ạ, nếu được thì giải thích giúp mình với nha, mình cảm ơn 

Câu 6: Để hàm số y=(1-m)x+3 nghịch biến trên R thì 1-m<0
=>m>1
=>Chọn B
Câu 7: D
Câu 10: (D)//(D')
=>\(\left\{{}\begin{matrix}3m+1=2\left(m+1\right)\\-2\ne-2\left(loại\right)\end{matrix}\right.\Leftrightarrow m\in\varnothing\)
=>Chọn D
Câu 11: \(x^2+2x+2=\left(x+1\right)^2+1>=1>0\forall x\)
=>\(\sqrt{x^2+2x+2}\) luôn xác định với mọi số thực x
=>Chọn A
Câu 12: Để hai đường thẳng y=x+3m+2 và y=3x+2m+3 cắt nhau tại một điểm trên trục tung thì \(\left\{{}\begin{matrix}1\ne3\left(đúng\right)\\3m+2=2m+3\end{matrix}\right.\)
=>3m+2=2m+3
=>m=1
=>Chọn C
Đúng 1
Bình luận (0)
Giải giúp mình nhanh được không ạ còn 30p nữa mik đi hc r ạ
Các bạn giúp mình giải với....rảnh thì có thể giải thích luôn hộ mình được không ạ?

Giải giúp mình bài 1, 2 với ạ, nếu được thì giải kĩ phần tính diện tích tam giác giúp mình, mình không hiểu phần đó
1.
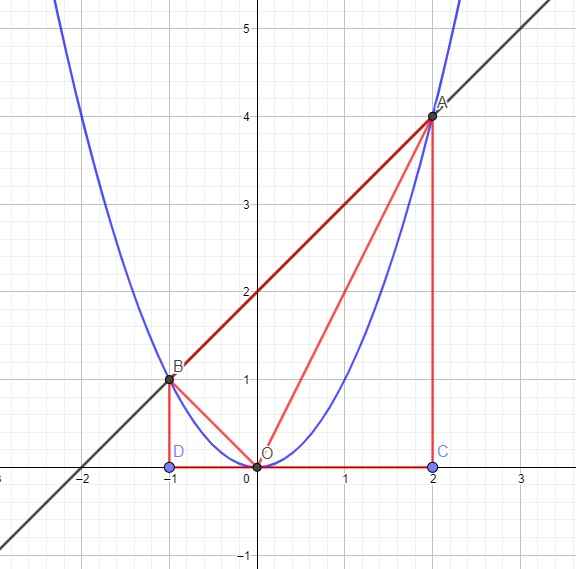
Dễ dàng tìm được tọa độ 2 giao điểm, do vai trò của A, B như nhau, giả sử \(A\left(2;4\right)\) và \(B\left(-1;1\right)\)
Gọi C và D lần lượt là 2 điểm trên trục Ox có cùng hoành độ với A và B, hay \(C\left(2;0\right)\) và \(D\left(-1;0\right)\)
Khi đó ta có ABDC là hình thang vuông tại D và C, các tam giác OBD vuông tại D và tam giác OAC vuông tại C
Độ dài các cạnh: \(BD=\left|y_B\right|=1\) ; \(AC=\left|y_A\right|=4\)
\(OD=\left|x_D\right|=1\) ; \(OC=\left|x_C\right|=2\) ; \(CD=\left|x_C-x_D\right|=3\)
Ta có:
\(S_{OAB}=S_{ABDC}-\left(S_{OBD}+S_{OAC}\right)\)
\(=\dfrac{1}{2}CD.\left(AC+BD\right)-\left(\dfrac{1}{2}BD.OD+\dfrac{1}{2}AC.OC\right)\)
\(=\dfrac{1}{2}.3.\left(4+1\right)-\left(\dfrac{1}{2}.1.1+\dfrac{1}{2}.4.2\right)=3\)
Đúng 1
Bình luận (0)

giải giúp mình câu 3 câu 4 với được không ạ
Câu 4:
Thay x=2 và y=-1 vào hệ, ta được:
\(\left\{{}\begin{matrix}2a-b=4\\2b+2=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=-2\\a=1\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Giải giúp mình với lời giải chi tiết ạ^^
Giải nhanh nhanh em tick cho ạ 
 Các bạn giải giúp mình với ạ, phần a ghi chi tiết bước giải hộ mình nhé. Mình cám ơn ạ! (Mai mình nộp rồi nên nhanh giúp mình ạ T.T)
Các bạn giải giúp mình với ạ, phần a ghi chi tiết bước giải hộ mình nhé. Mình cám ơn ạ! (Mai mình nộp rồi nên nhanh giúp mình ạ T.T)
a: ĐKXĐ: \(x\notin\left\{10;-10;\sqrt{10};-\sqrt{10}\right\}\)
b: \(A=\dfrac{5x^3+50x+2x^2+20+5x^3-50x-2x^2+20}{\left(x^2-10\right)\left(x^2+10\right)}\cdot\dfrac{x^2-100}{x^2+4}\)
\(=\dfrac{10x^3+40}{\left(x^2-10\right)\left(x^2+10\right)}\cdot\dfrac{x^2-100}{x^2+4}\)
Đúng 1
Bình luận (1)
Giúp mình các bài này với ạ mình cảm ơn các bạn không giải hết các bài cũng được 
ai giải thích giúp mình Tại sao không chọn được đáp án a với ạ
Xem thêm câu trả lời


