Trong mặt phẳng toạ độ, cho A(1;-1), B(3; 5), C(-2; 4). Tính diện tích tam giác ABC.
QL
Những câu hỏi liên quan
a) Tính khoảng cách từ gốc toạ độ C(0;0) đến điểm M(3 ; 4) trong mặt phẳng toạ độ Oxy.
b) Cho hai điểm I(a; b) và M(x ; y) trong mặt phẳng toạ độ Oxy. Nêu công thức tính độ dài đoạn thẳng IM.
a) Khoảng cách từ gốc tọa độ \(O\left( {0;0} \right)\) đến điểm \(M\left( {3;4} \right)\) trong mặt phẳng tọa độ Oxy là:
\(OM = \left| {\overrightarrow {OM} } \right| = \sqrt {{3^2} + {4^2}} = 5\)
b) Với hai điểm I(a; b) và M(x ; y) trong mặt phẳng toạ độ Oxy, ta có:\(IM = \sqrt {{{\left( {x - a} \right)}^2} + {{\left( {y - b} \right)}^2}} \)
Đúng 0
Bình luận (0)
Trong không gian với hệ toạ độ Oxyz, cho điểm M(3;2;1). Mặt phẳng (P) đi qua M và cắt các trục toạ độ Ox, Oy, Oz lần lượt tại các điểm A, B, C không trùng với gốc toạ độ sao cho M là trực tâm của tam giác ABC. Trong các mặt phẳng sau, tìm mặt phẳng song song với mặt phẳng (P).
Đọc tiếp
Trong không gian với hệ toạ độ Oxyz, cho điểm M(3;2;1). Mặt phẳng (P) đi qua M và cắt các trục toạ độ Ox, Oy, Oz lần lượt tại các điểm A, B, C không trùng với gốc toạ độ sao cho M là trực tâm của tam giác ABC. Trong các mặt phẳng sau, tìm mặt phẳng song song với mặt phẳng (P).
![]()
![]()
![]()
![]()
Đáp án A.
Gọi:
![]()
Phương trình mặt phẳng (P) có dạng:

Vì M là trực tâm của tam giác ABC nên
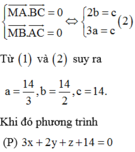
Đúng 0
Bình luận (0)
Trong không gian với hệ toạ độ Oxyz, cho điểm M(3;2;l). Mặt phẳng (P) đi qua M và cắt các trục toạ độ Ox,Oy,Oz lần lượt tại các điểm A, B, C không trùng với gốc toạ độ sao cho M là trực tâm của tam giác ABC. Trong các mặt phẳng sau, tìm mặt phẳng song song với mặt phẳng (P). A. 3x+2y+z+14 0 B. 2x+y+3z+9 0 C. 3x+2y+z-14 0 D. 2x+y+z-9 0
Đọc tiếp
Trong không gian với hệ toạ độ Oxyz, cho điểm M(3;2;l). Mặt phẳng (P) đi qua M và cắt các trục toạ độ Ox,Oy,Oz lần lượt tại các điểm A, B, C không trùng với gốc toạ độ sao cho M là trực tâm của tam giác ABC. Trong các mặt phẳng sau, tìm mặt phẳng song song với mặt phẳng (P).
A. 3x+2y+z+14= 0
B. 2x+y+3z+9= 0
C. 3x+2y+z-14= 0
D. 2x+y+z-9= 0
Trong mặt phẳng toạ độ Oxy, cho ba điểm A(2;3), B(-1; 1), C(3;- 1).
a) Tìm toạ độ điểm M sao cho\(\overrightarrow {AM{\rm{ }}} = {\rm{ }}\overrightarrow {BC} \).
b) Tìm toạ độ trung điểm N của đoạn thẳng AC. Chứng minh\(\overrightarrow {BN} {\rm{ }} = {\rm{ }}\overrightarrow {NM} \).
a) Gọi \(M\left( {a;b} \right) \Rightarrow \overrightarrow {AM} = \left( {a - 2;b - 3} \right)\)
Tọa độ vecto \(\overrightarrow {BC} = \left( {4; - 2} \right)\)
Để \(\overrightarrow {AM{\rm{ }}} = {\rm{ }}\overrightarrow {BC} \Leftrightarrow \left\{ \begin{array}{l}a - 2 = 4\\b - 3 = - 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 6\\b = 1\end{array} \right.\)
Vậy để \(\overrightarrow {AM{\rm{ }}} = {\rm{ }}\overrightarrow {BC} \) thì tọa độ điểm M là:\(M\left( {6;1} \right)\)
b) Gọi \(N\left( {x,y} \right) \Rightarrow \overrightarrow {NC} = \left( {3 - x, - 1 - y} \right)\)và \(\overrightarrow {AN} = \left( {x - 2,y - 3} \right)\)
Do N là trung điểm AC nên \(\overrightarrow {AN} = \overrightarrow {NC} \Leftrightarrow \left\{ \begin{array}{l}x - 2 = 3 - x\\y - 3 = - 1 - y\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = \frac{5}{2}\\y = 1\end{array} \right.\) . Vậy \(N\left( {\frac{5}{2},1} \right)\)
Ta có: \(\overrightarrow {BN} {\rm{ }} = \left( { \frac{7}{2};0} \right)\) và \(\overrightarrow {NM} = \left( {\frac{{ 7}}{2};0} \right)\). Vậy \(\overrightarrow {BN} {\rm{ }} = {\rm{ }}\overrightarrow {NM} \)
Đúng 0
Bình luận (0)
Trong mặt phẳng toạ độ Oxy cho A=(1;-3), B= (2;1) .
Tìm toạ độ Vécto AB và toạ độ trung điểm I của đoạn thẳng AB.
Trong mặt phẳng toạ độ oxy cho A(-1;-2)B(3;2)C(4;1) A gpij I là trung điểm của AB tìm toạ độ của I B gọi G là trọng tâm của tam giác ABC tìm toạ độ trọng tâm
a) Ta có: I là trung điểm AB
\(\Rightarrow\left\{{}\begin{matrix}x_I=\dfrac{x_A+x_B}{2}=\dfrac{-1+3}{2}=1\\y_I=\dfrac{y_A+y_B}{2}=\dfrac{-2+2}{2}=0\end{matrix}\right.\)
\(\Rightarrow I\left(1;0\right)\)
b) Ta có: G là trọng tâm tam giác ABC
\(\Rightarrow\left\{{}\begin{matrix}x_G=\dfrac{x_A+x_B+x_C}{3}=\dfrac{-1+3+4}{3}=2\\y_G=\dfrac{y_A+y_B+y_C}{3}=\dfrac{-2+2+1}{3}=\dfrac{1}{3}\end{matrix}\right.\)
\(\Rightarrow G\left(2;\dfrac{1}{3}\right)\)
Đúng 1
Bình luận (0)
Trong mặt phẳng toạ độ Oxy cho tam giác ABC có A(1;1) , B(2;-1) , C(3;3) . Toạ độ điểm E để tứ giác ABCE là hình bình hành là
Gọi E(x;y) \(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AB}=\left(1;-2\right)\\\overrightarrow{EC}=\left(3-x;3-y\right)\end{matrix}\right.\)
Tứ giác ABCE là hbh khi \(\overrightarrow{AB}=\overrightarrow{EC}\)
\(\Leftrightarrow\left\{{}\begin{matrix}3-x=1\\3-y=-2\end{matrix}\right.\) \(\Rightarrow E\left(2;5\right)\)
Đúng 1
Bình luận (0)
Trong mặt phẳng toạ độ Oxy, cho điểm M(-1; 3).
a) Tìm toạ độ điểm A đối xứng với điểm M qua gốc O.
b) Tìm toạ độ điểm B đối xứng với điểm M qua trục Ox.
c) Tìm toạ độ điểm C đối xứng với điểm M qua trục Oy.
a) Dựa vào hình vẽ ta thấy \(A\left( {1; - 3} \right)\)
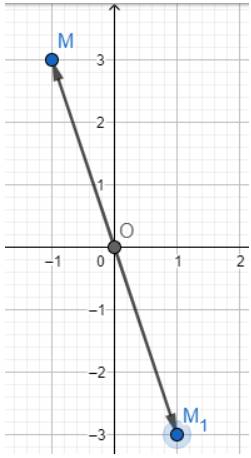
b) Dựa vào hình vẽ ta thấy \(B\left( { - 1; - 3} \right)\)

c) Dựa vào hình vẽ ta thấy \(C\left( {1;3} \right)\)
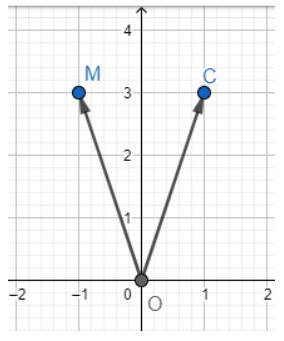
Đúng 0
Bình luận (0)
1. Trong mặt phẳng với hệ toạ độ Oxy, viết phương trình đường thẳng △ song song với đường thẳng d: 2x-y+2015=0 và cắt hai trục toạ độ tại M và N sao cho MN=3√5
2.Trong mặt phẳng với hệ toạ độ Oxy, cho 2 điểm A(1;2) ; B(4;3). Tìm toạ độ điểm M sao cho ∠MAB=135 độ và khoảng cách từ M đến đường thẳng AB bằng √10/2
Câu 1:
Do \(\Delta\) song song d nên nhận \(\left(2;-1\right)\) là 1 vtpt
Phương trình \(\Delta\) có dạng: \(2x-y+c=0\) (\(c\ne2015\))
Tọa độ giao điểm của \(\Delta\) và Ox: \(\left\{{}\begin{matrix}y=0\\2x-y+c=0\end{matrix}\right.\) \(\Rightarrow M\left(-\frac{c}{2};0\right)\)
Tọa độ giao điểm \(\Delta\) và Oy: \(\left\{{}\begin{matrix}x=0\\2x-y+c=0\end{matrix}\right.\) \(\Rightarrow N\left(0;c\right)\)
\(\overrightarrow{MN}=\left(\frac{c}{2};c\right)\Rightarrow\frac{c^2}{4}+c^2=45\Leftrightarrow c^2=36\Rightarrow\left[{}\begin{matrix}c=6\\c=-6\end{matrix}\right.\)
Có 2 đường thẳng thỏa mãn: \(\left[{}\begin{matrix}2x-y+6=0\\2x-y-6=0\end{matrix}\right.\)
Bài 2:
Bạn tham khảo ở đây:
Câu hỏi của tôn hiểu phương - Toán lớp 10 | Học trực tuyến
Đúng 0
Bình luận (0)
Trong không gian với hệ toạ độ Oxyz, mặt phẳng qua A(2;1;-1) và song song với hai trục toạ độ Ox,Oy là
A. z+1=0.
B. z-1=0.
C. x+y-3=0.
D. x-y-1=0.





