So sánh:
a) \(C_6^2\) và \(C_6^4\)
b) \(C_4^2 + C_4^3\) và \(C_5^3\)
\(C_1=1\mu F\) \(C_2=C_3=2\mu F\) \(C_4=C_5=3\mu F\) \(C_6=4\mu F\) \(C_7=6\mu F\)
\(U_{AB}=50\left(V\right)\)
a) Tính C bộ
b) Tình U, Q từng tụ
Tính: a) \(C_4^0 + C_4^1 + C_4^2 + C_4^3 + C_4^4\) b)\(C_5^0 - C_5^1 + C_5^2 - C_5^3 + C_5^4 - C_5^5\)
a) \(C_4^0 + C_4^1 + C_4^2 + C_4^3 + C_4^4 = {\left( {1 + 1} \right)^4} = {2^4} = 16\)
b) \(C_5^0 - C_5^1 + C_5^2 - C_5^3 + C_5^4 - C_5^5 = {\left( {1 - 1} \right)^5} = {0^5} = 0\)
Tìm số hạng tổng quát của cấp số cộng \(\left( {{c_n}} \right)\) có \({c_4} = 80\) và \({c_6} = 40\).
Giả sử cấp số cộng \(\left(c_n\right)\) có số hạng đầu \(c_1\) và công sai d.
Ta có:
\(c_4=c_1+\left(4-1\right)d=c_1+3d\Leftrightarrow c_1+3d=80\left(1\right)\\ c_6=c_1+\left(6-1\right)d=c_1+5d\Leftrightarrow c_1+5d=40\left(2\right)\)
Từ (1) và (2) ta có hệ phương trình:
\(\left\{{}\begin{matrix}c_1+3d=80\\c_1+5d=40\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}c_1=140\\d=-20\end{matrix}\right.\)
Vậy số hạng tổng quát của cấp số cộng \(\left(c_n\right)\) là:
\(c_n=c_1+\left(n-1\right)d=140+\left(n-1\right)\left(-20\right)=160-20\)
Sử dụng công thức nhị thức Newton, chứng tỏ rằng
a) \(C_4^0 + 2C_4^1 + {2^2}C_4^2 + {2^3}C_4^3 + {2^4}C_4^4 = 81\)
b) \(C_4^0 - 2C_4^1 + {2^2}C_4^2 - {2^3}C_4^3 + {2^4}C_4^4 = 1\)
a)
\(\begin{array}{l}C_4^0 + 2C_4^1 + {2^2}C_4^2 + {2^3}C_4^3 + {2^4}C_4^4\\ = {1^4}.C_4^0 + {1^3}.2C_4^1 + {1^2}{.2^2}C_4^2 + {1.2^3}C_4^3 + {2^4}C_4^4\\ = {\left( {1 + 2} \right)^4} = {3^4}\end{array}\)
\( = 81\) (đpcm)
b)
\(\begin{array}{l}C_4^0 - 2C_4^1 + {2^2}C_4^2 - {2^3}C_4^3 + {2^4}C_4^4\\ = {1^4}.C_4^0 - {1^3}.2C_4^1 + {1^2}{.2^2}C_4^2 - {1.2^3}C_4^3 + {2^4}C_4^4\\ = {\left( {1 - 2} \right)^4} = {\left( { - 1} \right)^4}\end{array}\)
\( = 1\) (đpcm)
Cho \(C_1=1\mu F\) \(C_2=5\mu F\) \(C_3=6\mu F\) \(C_4=4\mu F\) \(C_5=10\mu F\)
a) Tính điện dung của bộ
b) \(Q_1=2.10^{-6}\) (C). Tìm điện tích và hiệu điện thế của mỗi tụ
Cho mạch: \(C_1=2\mu F,C_2=4\mu F,C_3=C_4=6\mu F,U=120V\)
a) Tính \(C_b\)
b) Tính hiệu điện thế và điện tích mỗi tụ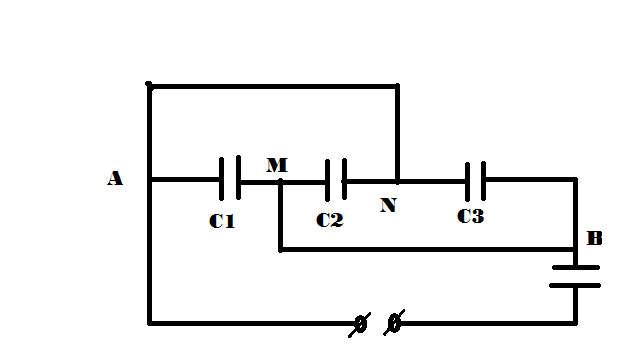
(C1//C2//C3)ntC4
a) Cb = 4 \(\mu\)F
b) U4 = 80 (V); Q4 = Qb = 4,8.10-4 (C)
U1 = U2 = U3 = 40 (V) ...
Các bạn học sinh lớp 11A1 trả lời 40 câu hỏi trong một bài kiểm tra. Kết quả được thống kê ở bảng sau:
a) Tính giá trị đại diện \({c_i},1 \le i \le 5\), của từng nhóm số liệu.
b) Tính \({n_1}{c_1} + {n_2}{c_2} + {n_3}{c_3} + {n_4}{c_4} + {n_5}{c_5}\).
c) Tính \(\bar x = \frac{{{n_1}{c_1} + {n_2}{c_2} + {n_3}{c_3} + {n_4}{c_4} + {n_5}{c_5}}}{{40}}\).
a)
\(\begin{array}{l}{c_1} = \frac{{16 + 21}}{2} = 18,5;{c_2} = \frac{{21 + 26}}{2} = 23,5;{c_3} = \frac{{26 + 31}}{2} = 28,5;\\{c_4} = \frac{{31 + 36}}{2} = 33,5;{c_3} = \frac{{36 + 41}}{2} = 38,5\end{array}\)
b) \({n_1}{c_1} + {n_2}{c_2} + {n_3}{c_3} + {n_4}{c_4} + {n_5}{c_5} = 4.18,5 + 6.23,5 + 8.28,5 + 18.33,5 + 4.38,5 = 1200\).
c) \(\bar x = \frac{{{n_1}{c_1} + {n_2}{c_2} + {n_3}{c_3} + {n_4}{c_4} + {n_5}{c_5}}}{{40}} = \frac{{1200}}{{40}} = 30\).
Trongg khai triển nhị thức Newton của \({(2 + 3x)^4}\), hệ số của \({x^2}\) là:
A. 9
B. \(C_4^2\)
C. \(9C_4^2\)
D. \(36C_4^2\)
Ta có:
\({(2 + 3x)^4} = C_4^0{2^4} + C_4^1{2^3}3x + C_4^2{2^2}{\left( {3x} \right)^2} + C_4^32.{\left( {3x} \right)^3} + C_4^4{\left( {3x} \right)^4}\)
=> Hệ số của của \({x^2}\)là \(C_4^2{.2^2}{.3^2} = 36C_4^2.\)
Chọn D.
Tính và so sánh:
a) \({( - 3)^2}.{( - 3)^4}\) và \({( - 3)^6}\);
b) \(0,6{}^3:0,{6^2}\) và \(0,{6}\)
a)
\(\begin{array}{l}{( - 3)^2}.{( - 3)^4} = 9.81 = 729\\ {( - 3)^6} = ( - 3).( - 3).( - 3).( - 3).( - 3).( - 3)\\ = 9.9.9 = 729\end{array}\)
Vậy \({( - 3)^2}.{( - 3)^4}\) = \({( - 3)^{6}}\)
b)
\(\begin{array}{l}0,6{}^3:0,{6^2} = 0,216:0,36 = 0,6\end{array}\)
Vậy \(0,6{}^3:0,{6^2}\) = \(0,{6}\)