Trong mặt phẳng Oxy, cho đường thẳng \(\Delta \) đi qua điểm \({M_0}\left( {{x_0};{y_0}} \right)\) và nhận \(\overrightarrow u = \left( {{u_1};{u_2}} \right)\) là vectơ chỉ phương. Với mỗi điểm \(M\left( {x;y} \right)\) thuộc \(\Delta \), tìm tọa độ của điểm M theo tọa độ của \({M_0}\) và \(\overrightarrow u \)
QL
Những câu hỏi liên quan
Trong mặt phẳng Oxy, cho đường thẳng \(\Delta \) đi qua điểm \({M_0}\left( {{x_0};{y_0}} \right)\) và nhận \(\overrightarrow n = \left( {a;b} \right)\) làm vectơ pháp tuyến. Với mỗi điểm \(M\left( {x;y} \right)\) thuộc \(\Delta \), chứng tỏ rằng điểm \(M\left( {x;y} \right)\) có tọa độ thỏa mãn phương trình:
\(ax + by + c = 0\) (với \(c = - a{x_0} - b{y_0}\))
\(\Delta \) nhận vectơ \(\overrightarrow n = \left( {a;b} \right)\) làm vectơ pháp tuyến, suy ra vectơ chỉ phương của \(\Delta \) là \(\overrightarrow u = (b; - a)\)
M và \({M_0}\) thuộc đường thẳng \(\Delta \) nên \(\Delta \) nhận \({\overrightarrow {MM} _0}\)làm vectơ chỉ phương
\({\overrightarrow {MM} _0} = \left( {{x_0} - x;{y_0} - y} \right)\), suy ra \(\left\{ \begin{array}{l}{x_0} - x = b\\{y_0} - y = - a\end{array} \right. \Rightarrow \left\{ \begin{array}{l}x = {x_0} - b\\y = {y_0} + a\end{array} \right.\)
Suy ra \(M\left( {{x_0} - {u_1};{y_0} - {u_2}} \right)\)
Thay tọa độ điểm M vào phương trình \(ax + by + c = 0\) ta có:
\(a\left( {{x_0} - b} \right) + b\left( {{y_0} + a} \right) + c = \left( { - ab + ba} \right) + \left( {a{x_0} + b{y_0} + c} \right) = 0\) (đúng vì \( - a{x_0} - b{y_0} = c\))
Vậy \(M(x;y)\) thỏa mãn phương trình đã cho
Đúng 0
Bình luận (0)
Trong mặt phẳng Oxy, cho hai đường thẳng Delta đi qua điểm {M_0}left( {{x_0};{y_0}} right) và vectơ overrightarrow n left( {a;b} right) và overrightarrow u left( {b; - a} right) khác vectơ 0. Cho biết overrightarrow u có giá song song hoặc trùng với Delta .a) Tính tích vô hướng overrightarrow n overrightarrow {.u} và nêu nhận xét về phương của hai vectơ overrightarrow n ,overrightarrow u b) Gọi Mleft( {x;y} right) là điểm di động trên Delta . Chứng tỏ rằng vectơ overrightarrow {{M_0}M} l...
Đọc tiếp
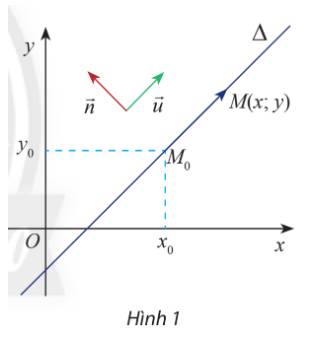
Trong mặt phẳng Oxy, cho hai đường thẳng \(\Delta \) đi qua điểm \({M_0}\left( {{x_0};{y_0}} \right)\) và vectơ \(\overrightarrow n = \left( {a;b} \right)\) và \(\overrightarrow u = \left( {b; - a} \right)\) khác vectơ 0. Cho biết \(\overrightarrow u \) có giá song song hoặc trùng với \(\Delta \).
a) Tính tích vô hướng \(\overrightarrow n \overrightarrow {.u} \) và nêu nhận xét về phương của hai vectơ \(\overrightarrow n ,\overrightarrow u \)
b) Gọi \(M\left( {x;y} \right)\) là điểm di động trên \(\Delta \). Chứng tỏ rằng vectơ \(\overrightarrow {{M_0}M} \) luôn cùng phương với vectơ \(\overrightarrow u \) và luôn vuông góc với vectơ \(\overrightarrow n \)
a) Ta có \(\overrightarrow n .\overrightarrow u = a.b + b.( - a) = 0\)
Tích vô hướng bằng 0 nên hai vectơ \(\overrightarrow n ,\overrightarrow u \)có phương vuông góc với nhau
b) Vectơ \(\overrightarrow {{M_0}M} \) có giá là đường thẳng \(\Delta\)
=> luôn cùng phương với vectơ \(\overrightarrow u \)
=> vectơ \(\overrightarrow {{M_0}M} \) có phương vuông góc với vectơ \(\overrightarrow n \)
Đúng 0
Bình luận (0)
Cho điểm {M_0}left( {{x_0};{y_0}} right) nằm trên đường tròn (C) tâm I(a;b)và cho điểmM(x;y) tùy ý trong mặt phẳng Oxy. Gọi Delta là tiếp tuyến với (C) tại {M_0}a) Viết biểu thức tọa độ của hai vt overrightarrow {{M_0}M} và overrightarrow {{M_0}I} b) Viết biểu thức tọa độ của tích vô hướng của hai vt overrightarrow {{M_0}M} và overrightarrow {{M_0}I} c) Phương trình overrightarrow {{M_0}M} .overrightarrow {{M_0}I} 0là phương trình của đường thẳng nào?
Đọc tiếp
Cho điểm \({M_0}\left( {{x_0};{y_0}} \right)\) nằm trên đường tròn \((C)\) tâm \(I(a;b)\)và cho điểm\(M(x;y)\) tùy ý trong mặt phẳng Oxy. Gọi \(\Delta \) là tiếp tuyến với \((C)\) tại \({M_0}\)
a) Viết biểu thức tọa độ của hai vt \(\overrightarrow {{M_0}M} \) và \(\overrightarrow {{M_0}I} \)
b) Viết biểu thức tọa độ của tích vô hướng của hai vt \(\overrightarrow {{M_0}M} \) và \(\overrightarrow {{M_0}I} \)
c) Phương trình \(\overrightarrow {{M_0}M} .\overrightarrow {{M_0}I} = 0\)là phương trình của đường thẳng nào?
a) Biểu thức tọa độ của hai vt \(\overrightarrow {{M_0}M} \) và \(\overrightarrow {{M_0}I} \) là \(\overrightarrow {{M_0}M} = \left( {x - {x_0};y - {y_0}} \right)\), \(\overrightarrow {{M_0}I} = \left( {a - {x_0};b - {y_0}} \right)\)
b) Ta có:
\(\overrightarrow {{M_0}M} .\overrightarrow {{M_0}I} = \left( {x - {x_0}} \right)\left( {a - {x_0}} \right) + \left( {b - {y_0}} \right)\left( {y - {y_0}} \right)\)
c) \(\overrightarrow {{M_0}M} .\overrightarrow {{M_0}I} = 0 \Rightarrow \overrightarrow {{M_0}M} \bot \overrightarrow {{M_0}I} \)
Mà \({M_0}I\) là đoạn thẳng nối tâm với điểm nằm ngoài
Vậy ta thấy pt đường thẳng \(M{M_0}\) là tiếp tuyến của đường tròn tại điểm \({M_0}\)
Đúng 0
Bình luận (0)
Trong mặt phẳng Oxy, cho đường tròn (C): \(\left(x-1\right)^2+y^2=2\) và đường thẳng \(\Delta:x-y+4=0\) gọi \(M\left(x_0;y_0\right)\) \(\in\) (C) là điểm có khoảng cách từ m tới (\(\Delta\)) lớn nhất. Tính \(x_0+y_0\)
Lập phương trình tham số của đường thẳng d đi qua điểm \(M_0\left(x_0;y_0;z_0\right)\) và vuông góc với mặt phẳng \(\left(P\right):Ax+By+Cz+D=0\) ?
Trong mặt phẳng Oxy. Cho đường thẳng Delta :ax + by + c 0left( {{a^2} + {b^2} 0} right) có vectơ pháp tuyến overrightarrow n và cho điểm {M_0}left( {{x_0};{y_0}} right)có hình chiếu vuông góc Hleft( {{x_H};{y_H}} right)trên Delta (hình 9).a) Chứng minh rằng hai vectơ overrightarrow n và overrightarrow {H{M_0}} cùng phương và tìm tọa độ của chúngb) Gọi p là tích vô hướng của hai vectơ overrightarrow n và overrightarrow {H{M_0}} .Chứng minh rằng p a{x_0} + b{y_0} + cc) Giải thích công thức...
Đọc tiếp
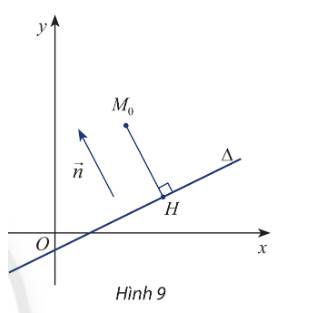
Trong mặt phẳng Oxy. Cho đường thẳng \(\Delta :ax + by + c = 0\left( {{a^2} + {b^2} > 0} \right)\) có vectơ pháp tuyến \(\overrightarrow n \) và cho điểm \({M_0}\left( {{x_0};{y_0}} \right)\)có hình chiếu vuông góc \(H\left( {{x_H};{y_H}} \right)\)trên \(\Delta \)(hình 9).
a) Chứng minh rằng hai vectơ \(\overrightarrow n \) và \(\overrightarrow {H{M_0}} \)cùng phương và tìm tọa độ của chúng
b) Gọi p là tích vô hướng của hai vectơ \(\overrightarrow n \) và \(\overrightarrow {H{M_0}} \).
Chứng minh rằng \(p = a{x_0} + b{y_0} + c\)
c) Giải thích công thức \(\left| {\overrightarrow {H{M_0}} } \right| = \frac{{\left| p \right|}}{{\left| {\overrightarrow n } \right|}}\)
a) Ta có: \(\overrightarrow n \) và \(\overrightarrow {H{M_0}} = \left( {{x_0} - {x_H};{y_0} - {y_H}} \right)\)
Mà H là hình chiếu vuông góc của \({M_0}\) trên \(\Delta \) nên \(H{M_0} \bot \Delta \)
Mặt khác vectơ pháp tuyến \(\overrightarrow n \) cùng vuông góc với \(\Delta \)
Suy ra \(\overrightarrow n \) và \(\overrightarrow {H{M_0}} \)cùng phương (đpcm)
b) Ta có: \(\overrightarrow n = (a;b)\) và \(\overrightarrow {H{M_0}} = \left( {{x_0} - {x_H};{y_0} - {y_H}} \right)\)
Suy ra \(p = \overrightarrow n .\overrightarrow {H{M_0}} = a\left( {{x_0} - {x_H}} \right) + b\left( {{y_0} - {y_H}} \right) = a{x_0} + b{y_0} - \left( {a{x_H} + b{y_H}} \right)\) (1)
Mà H thuộc đường thẳng \(\Delta \) nên tọa độ điểm H thỏa mãn phương trình đường thẳng \(\Delta \)
Thay tọa độ điểm H vào phương trình \(\Delta :ax + by + c = 0\left( {{a^2} + {b^2} > 0} \right)\) ta có:
\(a{x_H} + b{y_H} + c = 0 \Leftrightarrow c = - \left( {a{x_H} + b{y_H}} \right)\)
Thay \(c = - \left( {a{x_H} + b{y_H}} \right)\) vào (1) ta có
\(p = a{x_0} + b{y_0} + c\) (đpcm)
c) Ta có: \(p = \overrightarrow n .\overrightarrow {H{M_0}} \Leftrightarrow \overrightarrow {H{M_0}} = \frac{p}{{\overrightarrow n }} \Rightarrow \left| {\overrightarrow {H{M_0}} } \right| = \left| {\frac{p}{{\overrightarrow n }}} \right| \Rightarrow \left| {\overrightarrow {H{M_0}} } \right| = \frac{{\left| p \right|}}{{\left| {\overrightarrow n } \right|}}\)
Đúng 0
Bình luận (0)
Trong mặt phẳng toạ độ Oxy, cho đường thẳng Delta đi qua điểm {M_o}left( {{x_o};{y_o}} right) và có vectơ pháp tuyến overrightarrow n {rm{ }} left( {a;{rm{ }}b} right). Xét điểm M(x ; y) nằm trên Delta (Hình 28).a) Nhận xét về phương của hai vectơ overrightarrow n và overrightarrow {{M_o}M} .b) Tìm mối liên hệ giữa toạ độ của điểm M với toạ độ của điểm {M_o} và toạ độ của vectơ pháp tuyến overrightarrow n .
Đọc tiếp
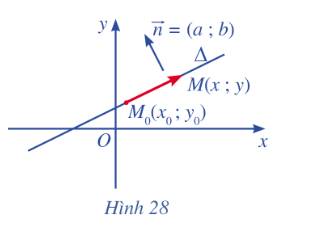
Trong mặt phẳng toạ độ Oxy, cho đường thẳng \(\Delta \) đi qua điểm \({M_o}\left( {{x_o};{y_o}} \right)\) và có vectơ pháp tuyến \(\overrightarrow n {\rm{ }} = \left( {a;{\rm{ }}b} \right)\). Xét điểm M(x ; y) nằm trên \(\Delta \) (Hình 28).
a) Nhận xét về phương của hai vectơ \(\overrightarrow n \) và \(\overrightarrow {{M_o}M} \).
b) Tìm mối liên hệ giữa toạ độ của điểm M với toạ độ của điểm \({M_o}\) và toạ độ của vectơ pháp tuyến \(\overrightarrow n \).
a) Phương của hai vecto \(\overrightarrow n \) và \(\overrightarrow {{M_o}M} \) vuông góc với nhau.
b) Ta có: \(\overrightarrow {{M_o}M} = \left( {x - {x_o};y - {y_o}} \right),\overrightarrow u = \left( {a;b} \right)\)
Xét điểm \(M\left( {x;y} \right) \in \Delta \). Vì \(\overrightarrow {{M_o}M} \bot \overrightarrow n \) nên: \(\overrightarrow {{M_o}M} .\overrightarrow n = 0 \Leftrightarrow a\left( {x - {x_o}} \right) + b\left( {y - {y_o}} \right) = 0 \Leftrightarrow ax + by - a{x_o} + b{y_o} = 0\)
Đúng 0
Bình luận (0)
Trong mặt phẳng toạ độ Oxy, cho đường thẳng Delta đi qua điểm {M_o}left( {{x_o};{y_o}} right) và có vectơ chỉ phươngoverrightarrow u {rm{ }} left( {a;{rm{ }}b} right) . Xét điểm M(x ; y) nằm trên Delta (Hình 26).a) Nhận xét về phương của hai vectơ overrightarrow u {rm{ }}vàoverrightarrow {{M_o}M} .b) Chứng minh có số thực t sao cho overrightarrow {{M_o}M} toverrightarrow u {rm{ }}.c) Biểu diễn toạ độ của điểm M qua toạ độ của điểm {M_o} và toạ độ của vectơ chỉ phương overrightarrow u {rm{...
Đọc tiếp
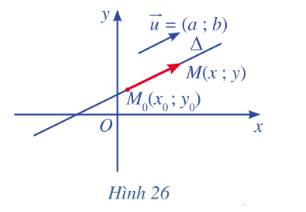
Trong mặt phẳng toạ độ Oxy, cho đường thẳng \(\Delta \) đi qua điểm \({M_o}\left( {{x_o};{y_o}} \right)\) và có vectơ chỉ phương\(\overrightarrow u {\rm{ }} = \left( {a;{\rm{ }}b} \right)\) . Xét điểm M(x ; y) nằm trên \(\Delta \) (Hình 26).
a) Nhận xét về phương của hai vectơ \(\overrightarrow u {\rm{ }}\)và\(\overrightarrow {{M_o}M} \) .
b) Chứng minh có số thực t sao cho \(\overrightarrow {{M_o}M} \) = \(t\overrightarrow u {\rm{ }}\).
c) Biểu diễn toạ độ của điểm M qua toạ độ của điểm \({M_o}\) và toạ độ của vectơ chỉ phương \(\overrightarrow u {\rm{ }}\).
a) Hai vectơ \(\overrightarrow u {\rm{ }}\)và \(\overrightarrow {{M_o}M} \)cùng phương với nhau.
b) Xét \(M\left( {x;y} \right)\). Vì cùng phương với nên có số thực t sao cho \(\overrightarrow {{M_o}M} = t\overrightarrow u {\rm{ }}\)
c) Do \(\overrightarrow {{M_o}M} = \left( {x - {x_o};y - {y_o}} \right),\overrightarrow u = \left( {a;b} \right)\) nên:
\(\overrightarrow {{M_o}M} = t\overrightarrow u {\rm{ }} \Leftrightarrow \left\{ \begin{array}{l}x - {x_o} = at\\y - {y_o} = bt\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = {x_o} + at\\y = {y_o} + bt\end{array} \right.\)
Vậy tọa độ điểm M là: \(M\left( {{x_o} + at;{y_o} + bt} \right)\)
Đúng 0
Bình luận (0)
Lập phương trình tham số của đường thẳng d đi qua điểm \(M_0\left(x_0;y_0;z_0\right)\) và song song với hai mặt phẳng cắt nhau :
\(\left(P\right):Ax+By+Cz+D=0\)
\(\left(Q\right):A'x+B'y+C'z+D=0\)



