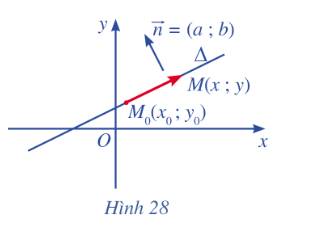
Trong mặt phẳng toạ độ Oxy, cho đường thẳng \(\Delta \) đi qua điểm \({M_o}\left( {{x_o};{y_o}} \right)\) và có vectơ chỉ phương\(\overrightarrow u {\rm{ }} = \left( {a;{\rm{ }}b} \right)\) . Xét điểm M(x ; y) nằm trên \(\Delta \) (Hình 26).
a) Nhận xét về phương của hai vectơ \(\overrightarrow u {\rm{ }}\)và\(\overrightarrow {{M_o}M} \) .
b) Chứng minh có số thực t sao cho \(\overrightarrow {{M_o}M} \) = \(t\overrightarrow u {\rm{ }}\).
c) Biểu diễn toạ độ của điểm M qua toạ độ của điểm \({M_o}\) và toạ độ của vectơ chỉ phương \(\overrightarrow u {\rm{ }}\).
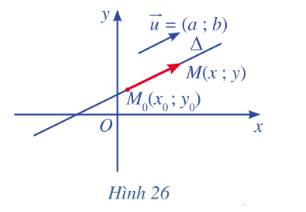
a) Hai vectơ \(\overrightarrow u {\rm{ }}\)và \(\overrightarrow {{M_o}M} \)cùng phương với nhau.
b) Xét \(M\left( {x;y} \right)\). Vì cùng phương với nên có số thực t sao cho \(\overrightarrow {{M_o}M} = t\overrightarrow u {\rm{ }}\)
c) Do \(\overrightarrow {{M_o}M} = \left( {x - {x_o};y - {y_o}} \right),\overrightarrow u = \left( {a;b} \right)\) nên:
\(\overrightarrow {{M_o}M} = t\overrightarrow u {\rm{ }} \Leftrightarrow \left\{ \begin{array}{l}x - {x_o} = at\\y - {y_o} = bt\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = {x_o} + at\\y = {y_o} + bt\end{array} \right.\)
Vậy tọa độ điểm M là: \(M\left( {{x_o} + at;{y_o} + bt} \right)\)