Tìm hợp lực của hai lực đối nhau \(\overrightarrow F \) và \( - \overrightarrow F \) (hình 11)
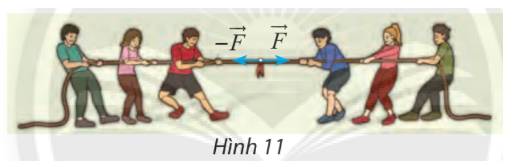
GIÚP MÌNH TÓM TẮT VÀ GIẢI CHI TIẾT VỚI Ạ![]()
Câu 14: Hai lực đồng quy \(\overrightarrow{F1}\) và \(\overrightarrow{F2}\) có độ lớn bằng 6 N và 8 N. Tìm độ lớn và hướng của hợp lực \(\overrightarrow{F}\)khi góc hợp bởi hướng của \(\overrightarrow{F1}\) và \(\overrightarrow{F1}\)là:
a. \(\alpha\) = 00\(^0\)
b. \(\alpha\) = 1800\(^{ }\)\(^0\)
c. \(\alpha\) = 900\(^0\)
d. \(\alpha\) = 60\(^0\)
<Tóm tắt bạn tự làm nhé>
a,\(F=\sqrt{F_1^2+F_2^2-2F_1F_2cos\alpha}=\sqrt{6^2+8^2-2\cdot6\cdot8\cdot cos0^o}=2\left(N\right)\)
b,\(F=\sqrt{F_1^2+F_2^2-2F_1F_2cos\alpha}=\sqrt{6^2+8^2-2\cdot6\cdot8\cdot cos180^o}=14\left(N\right)\)
c,\(F=\sqrt{F_1^2+F_2^2-2F_1F_2cos\alpha}=\sqrt{6^2+8^2-2\cdot6\cdot8\cdot cos90^o}=10\left(N\right)\)
d,\(F=\sqrt{F_1^2+F_2^2-2F_1F_2cos\alpha}=\sqrt{6^2+8^2-2\cdot6\cdot8\cdot cos60^o}=2\sqrt{13}\left(N\right)\)
Một lực \(\overrightarrow F \) không đổi tác động vào một vật và điểm đặt của lực chuyển động thẳng từ A đến B. Lực \(\overrightarrow F \) được phân tích thành hai lực thành phần là \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \) \((\overrightarrow F = \overrightarrow {{F_1}} + \overrightarrow {{F_2}} \;).\)
a) Dựa vào tính chất của tích vô hướng, hãy giải thích vì sao công sinh bởi lực \(\overrightarrow F \) (đã được đề cập ở trên) bằng tổng của các công sinh bởi các lực \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \).
b) Giả sử các lực thành phần \(\overrightarrow {{F_1}} \), \(\overrightarrow {{F_2}} \)tương ứng cùng phương, vuông góc với phương chuyển động của vật. Hãy tìm mối quan hệ giữa các công sinh bởi lực \(\overrightarrow F \) và lực \(\overrightarrow {{F_1}} \).
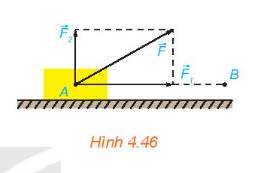
Tham khảo:
a)
Gọi \(A,{A_1},{A_2}\) lần lượt là công sinh bởi lực \(\overrightarrow F \), \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \).
Ta cần chứng minh: \(A = {A_1} + {A_2}\)
Xét lực \(\overrightarrow F \), công sinh bởi lực \(\overrightarrow F \) là: \(A = \left| {\overrightarrow F } \right|.{\rm{ AB}}.\cos \left( {\overrightarrow F ,\overrightarrow {AB} } \right) = \overrightarrow F .\overrightarrow {AB} \)
Tương tự, ta có: \({A_1} = \overrightarrow {{F_1}} .\overrightarrow {AB} \), \({A_2} = \overrightarrow {{F_2}} .\overrightarrow {AB} \)
Áp dụng tính chất của tích vô hướng ta có:
\({A_1} + {A_2} = \overrightarrow {{F_1}} .\overrightarrow {AB} + \overrightarrow {{F_2}} .\overrightarrow {AB} = \left( {\overrightarrow {{F_1}} + \overrightarrow {{F_2}} } \right).\overrightarrow {AB} = \overrightarrow F .\overrightarrow {AB} = A\)
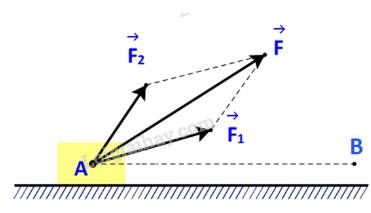
b)
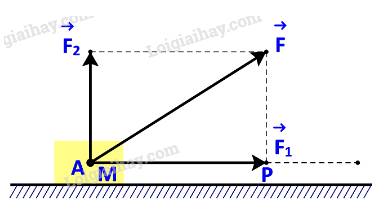
Vì \(\overrightarrow {{F_2}} \)tương ứng vuông góc với phương chuyển động nên \(\overrightarrow {{F_2}} \bot \overrightarrow {AB} \)
Do đó: công sinh bởi lực \(\overrightarrow {{F_2}} \) là: \({A_2} = \overrightarrow {{F_2}} .\overrightarrow {AB} = 0\)
Mà \(A = {A_1} + {A_2}\)
\( \Rightarrow A = {A_1}\)
Vậy công sinh bởi lực \(\overrightarrow F \) bằng công sinh bởi lực \(\overrightarrow {{F_1}} \).
Khi máy bay nghiêng cánh một góc \(\alpha \), lực \(\overrightarrow F \) của không khí tác động vuông góc với cánh và bằng tổng của lực nâng \(\overrightarrow {{F_1}} \) và lực cản \(\overrightarrow {{F_2}} \) (Hình 16). Cho biết \(\alpha = 30^\circ \)và \(\left| {\overrightarrow F } \right| = a\). Tính \(\left| {\overrightarrow {{F_1}} } \right|\) và \(\left| {\overrightarrow {{F_2}} } \right|\) theo a.

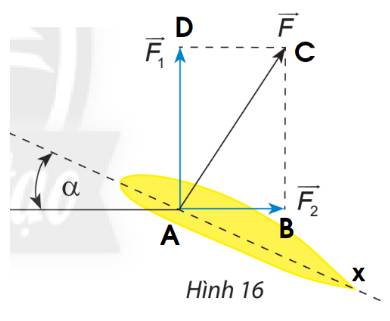
Khi đó các lực \(\overrightarrow F ,\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} \) lần lượt là \(\overrightarrow {AC} ,\overrightarrow {AD} ,\overrightarrow {AB} \)
\(\alpha = \widehat {{\rm{BAx}}} = 30^\circ \) \( \Rightarrow \widehat {CAB} = 60^\circ \)
\(AB = AC.c{\rm{os}}\widehat {CAB} = a.c{\rm{os60}}^\circ {\rm{ = }}\frac{a}{2} \Rightarrow \left| {\overrightarrow {{F_2}} } \right| = \left| {\overrightarrow {AB} } \right| = \frac{a}{2}\)
\(AD = BC = AC.\sin \widehat {CAB} = a.\sin 60^\circ = \frac{{a\sqrt 3 }}{2} \Rightarrow \left| {\overrightarrow {{F_1}} } \right| = \left| {\overrightarrow {AD} } \right| = AD = \frac{{a\sqrt 3 }}{2}\)
Vậy \(\left| {\overrightarrow {{F_1}} } \right| = \frac{{a\sqrt 3 }}{2};\left| {\overrightarrow {{F_2}} } \right| = \frac{a}{2}\)
Chọn câu trả lời đầy đủ nhất.
A. Momen của lực \(\overrightarrow{\text{F}}\) đối với trục quay là tích của lực với cánh tay đòn.
B. Momen của lực \(\overrightarrow{\text{F}}\) đối với trục quay là đại lượng đo bằng tích của lực với cánh tay đòn.
C. Momen của lực \(\overrightarrow{\text{F}}\) đối với trục quay là đại lượng đặc trưng cho tác dụng làm quay và được đo bằng tích độ lớn của lực với cánh tay đòn.
D. Momen của lực \(\overrightarrow{\text{F}}\) đối với trục quay là đại lượng đặc trưng cho tác dụng làm quay cản lực quanh trục ấy và được đo bằng tích độ lớn của lực với cánh tay đòn.
Một người dùng một lực \(\overrightarrow F \) có độ lớn là 90 N làm một vật dịch chuyển một đoạn 100 m. Biết lực hợp \(\overrightarrow F \) với hướng dịch chuyển là một góc \(60^\circ \). Tính công sinh bởi lực \(\overrightarrow F \)
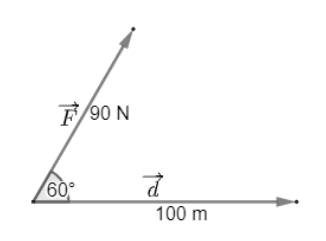
Công sinh bởi lực \(\overrightarrow F \) được tính bằng công thức
\(A = \overrightarrow F .\overrightarrow d = \left| {\overrightarrow F } \right|.\left| {\overrightarrow d } \right|.\cos \left( {\overrightarrow F ,\overrightarrow d } \right) = 90.100.\cos 60^\circ = 4500\) (J)
Vậy công sinh bởi lực \(\overrightarrow F \) có độ lớn bằng 4500 (J)
Một người dùng một lực \(\overrightarrow F \) có độ lớn là 20 N kéo một vật dịch chuyển một đoạn 50 m cùng hướng với \(\overrightarrow F \). Tính công sinh bởi lực \(\overrightarrow F \).
Gọi vectơ dịch chuyển của vật là \(\overrightarrow d \), ta có \(|\overrightarrow d |\; = 50\).
Theo giả thiết \(\overrightarrow F \) và \(\overrightarrow d \) cùng hướng nên \(\left( {\overrightarrow F ,\overrightarrow d } \right) = 0^\circ \)
Công sinh ra bởi lực \(\overrightarrow F \)được tính bằng:
\(A = \overrightarrow F .\overrightarrow d = \left| {\overrightarrow F } \right|.\left| {\overrightarrow d } \right|.\cos \left( {\overrightarrow F ,\overrightarrow d } \right) = 20.50.\cos 0^\circ = 1000\) (J)
Một người dùng một lực \(\overrightarrow F \) có cường độ là 10 N kéo một chiếc xe đi quãng đường dài 100 m. Tính công sinh bởi lực \(\overrightarrow F \), biết rằng góc giữa vectơ \(\overrightarrow F \) và hướng di chuyển là \(45^\circ \). (Công A (đơn vị: J) bằng tích của ba đại lượng: cường độ của lực \(\overrightarrow F \), độ dài quãng đường và côsin các góc giữa vectơ \(\overrightarrow F \) và độ dịch chuyển \(\overrightarrow d \)).
Theo giả thiết ta có: \(A = \left| {\overrightarrow F } \right|.\left| {\overrightarrow d } \right|.\cos \left( {\overrightarrow F ,\overrightarrow d } \right)\)
\( \Rightarrow A = 10.100.\cos 45^\circ = 500\sqrt 2 \left( J \right)\)
Vậy công sinh bởi lực \(\overrightarrow F \) là \(500\sqrt 2 \) (J)
Hình 4.19 biểu diễn hai lực \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} \) cùng tác động lên một vật, cho \(\left| {\overrightarrow {{F_1}} } \right| = 3\;N,\;\left| {\overrightarrow {{F_2}} } \right| = 2\;N.\) Tính độ lớn của hợp lực \(\overrightarrow {{F_1}} + \overrightarrow {{F_2}} \).
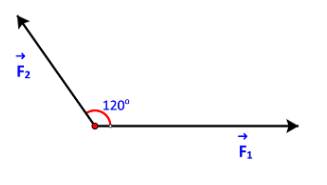
Tham khảo:
Dựng hình bình hành ABCD với hai cạnh là hai vectơ \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} \) như hình vẽ
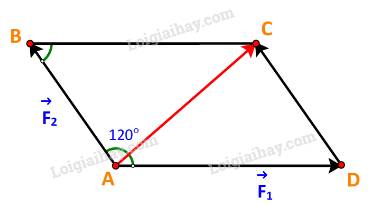
Ta có:
\(\overrightarrow {{F_1}} + \overrightarrow {{F_2}} = \overrightarrow {AD} + \overrightarrow {AB} = \overrightarrow {AC} \Rightarrow \left| {\overrightarrow {{F_1}} + \overrightarrow {{F_2}} } \right| = \left| {\overrightarrow {AC} } \right| = AC\)
Xét \(\Delta ABC\) ta có:
\(BC = AD = \left| {\overrightarrow {{F_1}} } \right| = 3\;,AB = \;\left| {\overrightarrow {{F_2}} } \right| = 2\;.\)
\(\widehat {ABC} = {180^o} - \widehat {BAD} = {180^o} - {120^o} = {60^o}\)
Theo định lí cosin ta có:
\(\begin{array}{l}A{C^2} = A{B^2} + B{C^2} - 2.AB.BC.\cos \widehat {ABC}\\ \Leftrightarrow A{C^2} = {2^2} + {3^2} - 2.2.3.\cos {60^o}\\ \Leftrightarrow A{C^2} = 7\\ \Leftrightarrow AC = \sqrt {7} \end{array}\)
Vậy \(\left| {\overrightarrow {{F_1}} + \overrightarrow {{F_2}} } \right| = \sqrt {7} \)
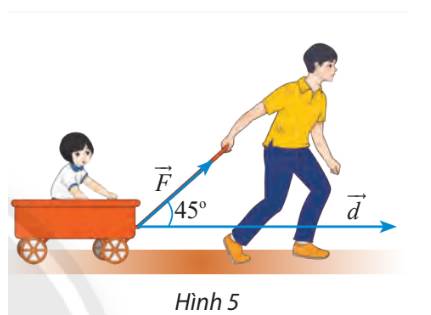
Một xe goòng được kéo bởi một lực \(\overrightarrow F \) có độ lớn là là 50 N, di chuyển theo quãng đường từ A đến B có chiều dài là 200 m. Cho biết góc giữa lực \(\overrightarrow F \) và \(\overrightarrow {AB} \) là \(30^\circ \) và \(\overrightarrow F \) được phân tích thành 2 lực \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} \) (hình 3). Tính công sinh ra bởi các lực \(\overrightarrow F ,\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \).
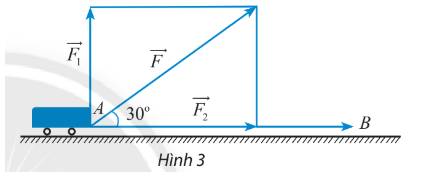
Ta xác định được các độ lớn:
\(\left| {\overrightarrow F } \right| = 50,\left| {\overrightarrow {{F_2}} } \right| = \left| {\overrightarrow F } \right|\cos 30^\circ = 50.\frac{{\sqrt 3 }}{2} = 25\sqrt 3 ,\left| {\overrightarrow {{F_1}} } \right| = \left| {\overrightarrow F } \right|.\sin 30^\circ = 50.\frac{1}{2} = 25\) (N)
Dựa vào hình vẽ ta có: \(\left( {\overrightarrow F ,\overrightarrow d } \right) = 30^\circ ,\left( {\overrightarrow {{F_1}} ,\overrightarrow d } \right) = 90^\circ ,\left( {\overrightarrow {{F_2}} ,\overrightarrow d } \right) = 0^\circ \)
Áp dụng công thức tính công sinh ra bởi lực \(A = \overrightarrow F .\overrightarrow d \) ta có:
\(A = \overrightarrow F .\overrightarrow d = \left| {\overrightarrow F } \right|\left| {\overrightarrow d } \right|\cos \left( {\overrightarrow F ,\overrightarrow d } \right) = 50.200.\cos 30^\circ = 5000 (J)\)
\({A_1} = \overrightarrow {{F_1}} .\overrightarrow d = \left| {\overrightarrow {{F_1}} } \right|\left| {\overrightarrow d } \right|\cos \left( {\overrightarrow {{F_1}} ,\overrightarrow d } \right) = 25.200.\cos 90^\circ = 0 (J)\)
\({A_2} = \overrightarrow {{F_2}} .\overrightarrow d = \left| {\overrightarrow {{F_2}} } \right|\left| {\overrightarrow d } \right|\cos \left( {\overrightarrow {{F_2}} ,\overrightarrow d } \right) = 25\sqrt 3 .200.\cos 0^\circ = 5000\sqrt 3 (J)\)