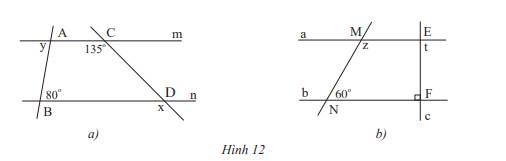
Cho biết m // n và a // b. Tính số đo x,y,z và t của các góc trong hình 12.
Bài 1: kể tên các cặp góc đối đỉnh và các cặp góc kề bù nếu có trong các hình sau:
a:
Đối đỉnh: góc tMx và góc yMz; góc tMy và góc xMz
Kề bù: góc tMz và góc tMy; góc yMz và góc xMz
b: Kề bù: góc MNA và góc MNx; góc MAN và góc zAM
c: Đối đỉnh: góc AIB và góc MIN; góc AIM và góc BIN
Kề bù: góc AIB và góc AIM
góc MIN và góc BIN
1. Biết rằng một tam giác có cả ba góc bằng nhau
- Hãy cho biết số đo các góc của tam giác đó
- Hãy cho biết số đo các góc ngoài của tam giác đó.

2. Xem hình trên. Với hình 1, tam giác đã cho là một tam giác vuông, có một góc nhọ là x và góc nhọn kia là 50o suy ra: x + 50o = 90o hay x = 40o
cho biết số đo các góc y, z, t, m trong mỗi hình vẽ ở hình trên
1. Biết rằng một tam giác có cả ba góc bằng nhau
- Hãy cho biết số đo các góc của tam giác đó
- Hãy cho biết số đo các góc ngoài của tam giác đó.
2. Xem hình trên. Với hình 1, tam giác đã cho là một tam giác vuông, có một góc nhọ là x và góc nhọn kia là 50o suy ra: x + 50o = 90o hay x = 40o
cho biết số đo các góc y, z, t, m trong mỗi hình vẽ ở hình trên
bài 1:
a) Gọi số đo các góc của tam giác trên là x; y; z; ta có:
x = y = z theo đề bài
x + y + z = 180 độ (tổng 3 góc trong tam giác)
=> x + x + x = 180 độ
x = 60 độ
vậy số đo 3 góc của tam giác trên cùng bằng 60 độ
b) số đo các góc ngoài của tam giác trên cùng bằng 180 độ - 60 độ = 120 độ
a) Cho biết các số đo x,y,t trong mỗi hình a),b),c)
b)Ko dùng thước đo góc, cho biết tổng số đo các góc của một HCN.
c)Ko dùng thước đo góc , cho biết tổng số đo các góc trong một hình tứ giác lồi.
d)Có hay ko một tam giác mà cả 3 góc đều lớn hơn 60độ?
e)Có hay ko một tam giác mà cả 3 góc đều nhỏ hơn 60ođộ?

Cho hình 1, biết: a ⊥ P Q ; b ⊥ P Q và N ^ = 75 0 .
Tính số đo x của góc M
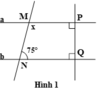
Ta có: a ⊥ P Q ; b ⊥ P Q (gt).
Þ a // b (vì cùng vuông góc với PQ).
Do đó: x + 75 ° = 180 ° (cặp góc trong cùng phía)
x = 180 ° − 75 ° = 105 ° .
B1:Tìm x , y , z biết ( giải chi tiết giúp mk nhé )
2x=3y=10z-2x-3y và x-y+z=-15
2x=3y=10z-2x và x-y +z = -33
B2: tính số đo các góc của tam giác ABC , biết số đo các góc A,B,C lần lượt tỉ lệ nghịch với 2,3,6
1)Tìm x,y,z biết x÷y÷z=2÷3÷4 và x+2y+z=36.
2)Cho tam giác ABC; 5Â=3B=15C. Tính số đo các góc tam giác ABC.
3)Tính số đo các góc của tam giác ABC, biết B-C=100 và C-A=100.
giúp mình giải với, ngày mai nộp bài rồi!!!!
a) Trong Hình 11, cho biết \(\Delta ABC\backsim\Delta A'B'C'\). Viết tỉ số của các cạnh tương ứng và chỉ ra các cặp góc tương ứng.

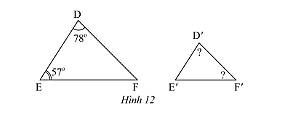
b) Trong Hình 12, cho biết \(\Delta DEF\backsim\Delta D'E'F'\). Tính số đo \(\widehat {D'}\) và \(\widehat F\).
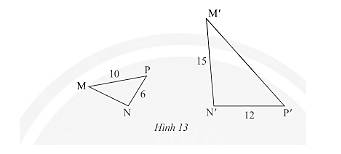
c) Trong Hình 12, cho biết \(\Delta MNP\backsim\Delta M'N'P'\). Tính độ dài các đoạn thẳng \(MN\) và \(MP'\).
a) Ta có: \(\Delta ABC\backsim\Delta A'B'C'\) thì \(\left\{ \begin{array}{l}\widehat A = \widehat {A'};\widehat B = \widehat {B'};\widehat C = \widehat {C'}\\\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}} = \frac{{B'C'}}{{BC}} = k\end{array} \right.\).
b) Xét tam giác \(DEF\) có:
\(\widehat D + \widehat E + \widehat F = 180^\circ \) (tổng ba góc trong một tam giác).
Ta có: \(\widehat D = 78^\circ ;\widehat E = 57^\circ \) thay số ta được
\(78^\circ + 57^\circ + \widehat F = 180^\circ \Rightarrow \widehat F = 180^\circ - 78^\circ - 57^\circ = 45^\circ \)
Ta có: \(\Delta DEF\backsim\Delta D'E'F' \Rightarrow \widehat D = \widehat {D'};\widehat E = \widehat {E'};\widehat F = \widehat {F'}\) (các góc tương ứng bằng nhau)
Do đó, \(\widehat D = \widehat {D'} = 78^\circ ;\widehat F = \widehat {F'} = 45^\circ \).
c) Ta có \(\Delta MNP\backsim\Delta M'N'P' \Rightarrow \frac{{MN}}{{M'N'}} = \frac{{MP}}{{M'P'}} = \frac{{NP}}{{N'P'}}\) (các cặp cạnh tương ứng có cùng tỉ lệ).
Với \(MP = 10;NP = 6;M'N' = 15;N'P' = 12\) thay vào ta được:
\( \Rightarrow \left\{ \begin{array}{l}\frac{{MN}}{{15}} = \frac{1}{2}\\\frac{{10}}{{M'P'}} = \frac{1}{2}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}MN = \frac{{15.1}}{2} = 7,5\\M'P' = \frac{{10.2}}{1} = 20\end{array} \right.\).
Vậy \(MN = 7,5;M'P' = 20\).
1/Cho góc A và góc B phụ nhau và A-B=25 độ. Tính góc A và B ?
2/Cho góc A và B bù nhau và A-B=30 độ. Tính số đo của góc A
3/
a/ Vẽ tam giác ABC, biết BC=4cm;AB=2cm;AC=3cm
b/ Vẽ tiếp đường tròn ( C;2cm); đường tròn này cắt cạnh AC tại M,cắt cạnh BC tại N, về các đoạn thẳng AN,MN.Hãy cho biết trên hình vẽ có bao nhiêu tam giác. Goi ten cac tam giac ay.
4/Với giá trị nào của x thuộc Z các phân số sau có giá trị là một số nguyên
B= (x-2) /(x + 3)