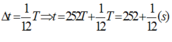Trên 2 trục số, so sánh khoảng cách từ điểm 0 đến hai điểm \(\sqrt 2 \) và \( - \sqrt 2 \).

Cho hai đường thẳng chéo nhau: d : x = 2 - t y = - 1 + t z = 1 - t d ' : x = 2 + 2 t y = t z = 1 + t
Lấy hai điểm M(2; -1; 1) và M'(2; 0; 1) lần lượt trên d và d'. Tính khoảng cách từ M đến mặt phẳng ( β) và khoảng cách từ M' đến mặt phẳng (α). So sánh hai khoảng cách đó.
a) Hãy biểu diễn hai số -5 và 5 trên cùng một trục số.
b) Tính khoảng cách từ điểm 5 đến điểm 0.
c) Tính khoảng cách từ điểm -5 đến điểm 0.
a)

b) Khoảng cách từ điểm 5 đến điểm 0 là: 5 đơn vị
c) Khoảng cách từ điểm - 5 đến điểm 0 là: 5 đơn vị
Trên mặt phẳng tọa độ Oxy, vẽ đồ thị (d) của hàm số y=-x+2
Tìm tọa độ của những điểm nàm trên đường thẳng (d) sao cho khoảng cách từ điểm đó đến trục Ox bằng hai lần khoảng cách từ điểm đó đến trục Oy
Tìm khoảng cách từ điểm 6 đến điểm -2 trên trục số.
Khoảng cách từ điểm 6 đến điểm -2 trên trục số là :
+( 6 + 2 ) = 8
Quan sát hai điểm biểu diễn các số hữu tỉ \(\frac{5}{4}\) và \(\frac{{ - 5}}{4}\) trên trục số sau:

Nêu nhận xét về khoảng cách từ hai điểm \(\frac{5}{4}\) và \(\frac{{ - 5}}{4}\) đến điểm 0.
Hai điểm biểu diễn các số hữu tỉ \(\frac{5}{4}\) và \(\frac{{ - 5}}{4}\) cách gốc 0 một khoảng bằng nhau.
Hai điểm sáng 1 và 2 cùng dao động điều hòa trên trục Ox với phương trình dao động ![]() cm (với
cm (với 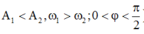 ). Tại thời điểm ban đầu t = 0 khoảng cách giữa hai điểm sáng là a3. Tại thời điểm t = ∆t hai điểm sáng cách nhau khoảng 2a, đồng thời chúng vuông pha. Đến thời điểm t = 2∆t thì điểm sáng 1 trở lại vị trí đầu tiên và khi đó hai điểm sáng cách nhau 3a3. Tỉ số
). Tại thời điểm ban đầu t = 0 khoảng cách giữa hai điểm sáng là a3. Tại thời điểm t = ∆t hai điểm sáng cách nhau khoảng 2a, đồng thời chúng vuông pha. Đến thời điểm t = 2∆t thì điểm sáng 1 trở lại vị trí đầu tiên và khi đó hai điểm sáng cách nhau 3a3. Tỉ số ![]() bằng
bằng
A. 3,0.
B. 2,5.
C. 3,5.
D. 4,0.
Đáp án B
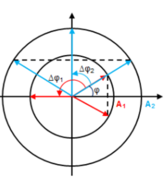
Biểu diễn hai dao động như hình vẽ.
- Tại t = 0 khoảng cách hai điểm sáng là
![]()
- Sau khoảng thời gian ∆t điểm sáng 1 quay được góc ![]() và điểm sáng 2 quay được góc
và điểm sáng 2 quay được góc ![]()
Do sau khoảng thời gian 2∆t điểm sáng 1 lại trở về vị trí ban đầu nên sau khoảng thời gian ∆t thì dao động 1 có pha là π rad.
Hai dao động khi đó vuông góc và điểm sáng 2 châm hơn nên vị trí được biểu diễn như hình.
Lúc này ta có khoảng cách giữa hai điểm sáng là A1 = 2a
- Sau khoảng thời gian 2∆t điểm sáng 1 quay được thêm một góc ![]() nữa và điểm sáng 2 quay được thêm một góc
nữa và điểm sáng 2 quay được thêm một góc ![]() nữa. Vị trí của chúng được biểu diễn như hình.
nữa. Vị trí của chúng được biểu diễn như hình.
Khoảng cách giữa chúng là

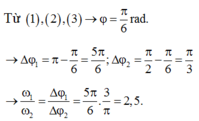
Hai điểm sáng 1 và 2 cùng dao động điều hòa trên trục Ox với phương trình dao động  (với
(với ![]() . Tại thời điểm ban đầu t = 0 khoảng cách giữa hai điểm sáng là a3. Tại thời điểm t = ∆t hai điểm sáng cách nhau khoảng 2a, đồng thời chúng vuông pha. Đến thời điểm t = 2∆t thì điểm sáng 1 trở lại vị trí đầu tiên và khi đó hai điểm sáng cách nhau 3a3. Tỉ số
. Tại thời điểm ban đầu t = 0 khoảng cách giữa hai điểm sáng là a3. Tại thời điểm t = ∆t hai điểm sáng cách nhau khoảng 2a, đồng thời chúng vuông pha. Đến thời điểm t = 2∆t thì điểm sáng 1 trở lại vị trí đầu tiên và khi đó hai điểm sáng cách nhau 3a3. Tỉ số ![]() bằng
bằng
A. 3,0
B. 2,5
C. 3,5
D. 4,0
Đáp án B
Biểu diễn hai dao động như hình vẽ.
- Tại ![]() khoảng cách hai điểm sáng là
khoảng cách hai điểm sáng là ![]()
- Sau khoảng thời gian ∆t điểm sáng 1 quay được góc ![]() và điểm sáng 2 quay được góc
và điểm sáng 2 quay được góc ![]()
Do sau khoảng thời gian 2∆t điểm sáng 1 lại trở về vị trí ban đầu nên sau khoảng thời gian ∆t thì dao động 1 có pha là π rad.
Hai dao động khi đó vuông góc và điểm sáng 2 châm hơn nên vị trí được biểu diễn như hình.
Lúc này ta có khoảng cách giữa hai điểm sáng là ![]()
- Sau khoảng thời gian 2∆t điểm sáng 1 quay được thêm một góc 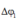 nữa và điểm sáng 2 quay được thêm một góc
nữa và điểm sáng 2 quay được thêm một góc ![]() nữa. Vị trí của chúng được biểu diễn như hình.
nữa. Vị trí của chúng được biểu diễn như hình. 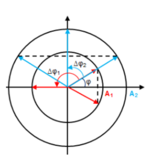
Khoảng cách giữa chúng là 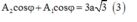
Từ 
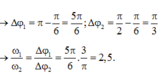
Bài 1: Cho hàm số y=f(x)=ax4-bx2+x+3. Biết f(2)=17. Tính f(-2)
Bài 2: Cho(d):y=-x+2
a) Vẽ (d)
b) Tìm các điểm nằm trên (d) sao cho khoảng cách từ điểm đó đến trục Ox bằng 2 làn khoảng cách từ đó đến trục Oy
Thực hiện giao thoa ánh sáng với khe I–âng. Nguồn sáng đơn sắc có bước sóng 500 nm, khoảng cách hai khe a =1 mm, khoảng cách từ mặt phẳng chứa hai khe đến màn quan sát D = 2 m, khoảng cách từ khe F đến mặt phẳng chứa hai khe là d =1 m. Cho khe F dao động điều hòa trên trục Ox vuông góc với trục đối xứng của hệ quanh vị trí O cách đều hai khe F1, F2với phương trình
.Trên màn, xét điểm M cách vân trung tâm một khoảng 1 mm. Tính cả thời điểm t = 0, điểm M trùng với vân sáng lần thứ 2018 vào thời điểm
A. 252(s)
B. 504+ 1/2 (s)
C. 252+ 1/6 (s)
D. 252+ 1/12 (s)
Đáp án D
Khi dịch chuyển nguồn theo phương song song với hai khe thì hệ vân (vân trung tâm ) dịch chuyển theo chiều ngược lại một đoạn :
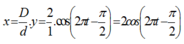
Chu kì dao động là : T = 1s.
Khoảng vân : 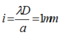
Điểm M cách vị trí trung tâm 1mm, vậy ban đầu khi t = 0 thì M là vân sáng.
Điểm M là vân sáng thì thỏa mãn : xM = ki
Ta thấy vân trung tâm sẽ dao động với biên độ 2 cm (từ phương trình), vậy điểm M sẽ là vân sáng khi vân trung tâm ở các vị trí có tọa độ x = 0, 1, 2, – 1, –2 cm
Vẽ đường tròn ta được:
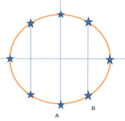
Các vị trí đánh dấu sao là các vị trí trong một chu kì chuyển động M là vân sáng. Ban đầu M nằm ở vị trí A. mỗi chu kì có 8 lần M là vân sáng
Vậy khi M à vân sáng lần thứ 2018 = 8.252 + 2 lần thì nó đã đi trong thời gian là : t = 252T + ∆t
Dễ thấy khi đi được 252 chu kì thì M đã quay lại A, vậy chỉ cần đi đến B là đã được thêm 2 lần nữa ( vì ban đầu khi t = 0 thì M ở A, nên nó là 1 vân sáng, đến lúc nó đến B được tính là lần nữa).
Thời gian đi hết cung AB là :