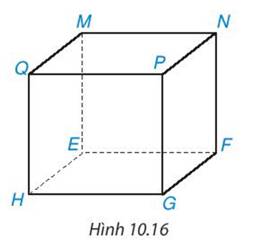
Kể tên các đỉnh, cạnh và đường chéo của hình lập phương MNPQ. EFGH ở Hình 10.16.
Quan sát hình 10.2 và gọi tên đỉnh, cạnh ,đường chéo, mặt đáy, mặt bên của hình lập phương MNPQ. ABCD.
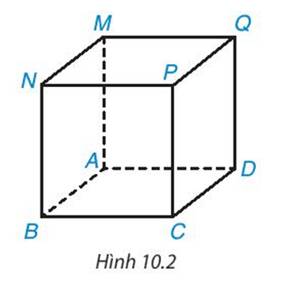
+ 8 đỉnh : A, B, C, D, M, N, Q, P.
+ 12 cạnh : AB, AD, BC, CD, MN, MQ, QP, PN, AM, BN, CP, DQ.
+ 4 đường chéo: ND, QB, MC, PA.
+ 4 mặt bên : AMNB, MQDA, PQDC, NPCB.
+ 2 mặt đáy: ABCD, MNPQ
Quan sát hình lập phương ở Hình 9, đọc tên các mặt, các cạnh, các đỉnh và các đường chéo của hình lập phương đó.
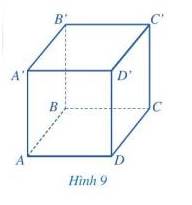
Hình lập phương ABCD. A’B’C’D’ có:
+) 6 mặt gồm: ABCD; A’B’C’D’; ABB’A’; ADD’A’; BCC’B’; CDD’C’.
+) 12 cạnh gồm: AB; BC;CD;DA;A’B’;B’C’;C’D’; D’A’; AA’; BB’; CC’ ; DD’.
+) 8 đỉnh gồm: A;B;C;D;A’;B’;C’;D’.
+) 4 đường chéo gồm: AC’; A’C; BD’; B’D
Các đỉnh: A,B,C,D,A',B',C',D'
Các cạnh: AB, BC, CD, DA, A'B', B'C', C'D', D'A' , AA', BB', CC', DD'
Các mặt: ABCD, A'B'C'D', ABB'A', CC'D'D, BCC'B', A'D'DA
Cho hình lập phương ABCD. EFGH cạnh 4cm Kể tên của các mặt hình lập phương ABCD. EFGH song song với đường thẳng EH.
Giúp mik với mik cần gấp
(ADC); (BCA); (BDC); (ADB)
(EFG); (FGH)
cho hình chóp S.MNPQ, đáy MNPQ là hình chữ nhật
a) kể tên đỉnh, các cạnh bên, cạnh đáy, mặt bên và mặt đáy của hình chóp
b) tìm giao tuyến của hai mặt phẳng (SPQ) và (MNPQ)
c) tìm giao tuyến của 2 mặt phẳng (SMQ) và (SQP)
trình bày cách vẽ tam giác MNO có cạnh 4 cm bằng thước và compa.
a) từ đó hãy vẽ hình lục giác đều MNPQRH ?
b)Kể tên các đỉnh , cạnh , góc , đường chéo chính của hình lục giác đều MNPQRH ?
c)Hãy nhận xét về độ dài các cạnh ,các đường chéo chính và độ lớn các góc của hình lục giác đều MNPQRH ?
Quan sát hình lăng trụ đứng tứ giác ở Hình 9, đọc tên các mặt, các cạnh, các đỉnh và các đường chéo của hình lăng trụ đứng tứ giác đó.
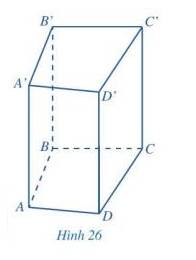
Hình lăng trụ đứng tứ giác ABCD. A’B’C’D’ có:
+) 6 mặt gồm: ABCD; A’B’C’D’; ABB’A’; ADD’A’; BCC’B’; CDD’C’.
+) 12 cạnh gồm: AB; BC;CD;DA;A’B’;B’C’;C’D’; D’A’; AA’; BB’; CC’ ; DD’.
+) 8 đỉnh gồm: A;B;C;D;A’;B’;C’;D’.
1.cho hình chóp S.MNPQ, đáy MNPQ là hình chữ nhật
a) kể tên đỉnh, các cạnh bên, cạnh đáy, mặt bên và mặt đáy của hình chóp
b) tìm giao tuyến của hai mặt phẳng (SPQ) và (MNPQ)
c) tìm giao tuyến của 2 mặt phẳng (SMQ) và (SQP)
Một)- Đỉnh của hình chóp S.MNPQ là điểm S.- Các cạnh bên của hình chóp là SM, SN, NP, NQ, PQ.- Cạnh đáy của hình chóp là đoạn thẳng MN, NP, PQ và QM.- Mặt bên của hình chóp là tam giác SMN, SNP, NQP và QMS.- Mặt đáy của hình chóp là hình chữ nhật MNPQ.b) Giao tuyến của hai mặt phẳng (SPQ) và (MNPQ) là một đường thẳng. Gọi đường thẳng này là d.c) Giao tuyến của hai mặt phẳng (SMQ) và (SQP) cũng là một đường thẳng. Gọi đường thẳng này là e.
Cho tứ giác MNPQ có E, F, G, H lần lượt là trung điểm của các cạnh MN,NP.PQ.PM.
a) Chứng Minh rằng EFGH là hình bình hành
b) Hai đường chéo của tứ giác MNPQ phải có điều kiện gid thì tứ giác EFGH là hình thang. Vẽ hình minh họa.
Quan sát hình thang cân ở hình 4.13a.
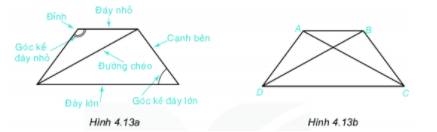
1. Gọi tên các đỉnh, đáy lớn, đáy nhỏ, đường chéo, cạnh bên và các góc kề đây lớn của hình thang cân ABCD (14.13b)
2. Sử dụng thước thẳng hoặc compa để so sánh hai cạnh bên, hai đường chéo của hình thang cân ABCD.
3. Hai đáy của hình thang cân ABCD có song song với nhau không?
4. Hai góc kề một đáy của hình thang cân ABCD có bằng nhau không?
1) Đỉnh: A, B, C, D
Đáy lớn: DC
Đáy nhỏ: AB
Đường chéo: AC, BD
Cạnh bên AD, BC
2) Dùng thước thẳng hoặc compa, ta đo được: AD = BC; AC = BD
Vậy: Hai cạnh bên hình thang cân bằng nhau
Hai đường chéo hình thang cân bằng nhau.
3) Khi đặt eke vuông góc với AB ta thấy eke cũng vuông góc với CD. Do đó AB và CD song song với nhau.
Vậy hai đáy của hình thang cân song song với nhau.
4) Hai góc kề một đáy của hình thang bằng nhau.