dạng lập bảng xét dấu max min với bất ptrinh lm ntn ạ
tìm min max của y = sin x trên đoạn \(\left[\frac{-\pi}{3};\frac{2\pi}{3}\right]\)
Cách lập bảng biến thiên để tìm min max ntn, chỉ rõ cách lập bảng biến thiên giúp mh đk k, cảm ơn nhé!
\(y'=cosx\) ; \(y'=0\Rightarrow cosx=0\Rightarrow x=\frac{\pi}{2}+k\pi\)
Do \(x\in\left[-\frac{\pi}{3};\frac{2\pi}{3}\right]\Rightarrow x=\frac{\pi}{2}\)
Không cần lập bảng biến thiên, chúng ta chỉ cần quan tâm 3 vị trí: 2 biên và điểm dừng vừa tìm được
\(y\left(\frac{\pi}{2}\right)=1\) ; \(y\left(-\frac{\pi}{3}\right)=-\frac{\sqrt{3}}{2}\) ; \(y\left(\frac{2\pi}{3}\right)=\frac{\sqrt{3}}{2}\)
So sánh 3 giá trị trên ta được:
\(y_{max}=1\) khi \(x=\frac{\pi}{2}\)
\(y_{min}=-\frac{\sqrt{3}}{2}\) khi \(x=-\frac{\pi}{3}\)
Mn ơi giúp mình lập bảng xét dấu với ạ mơn nhiều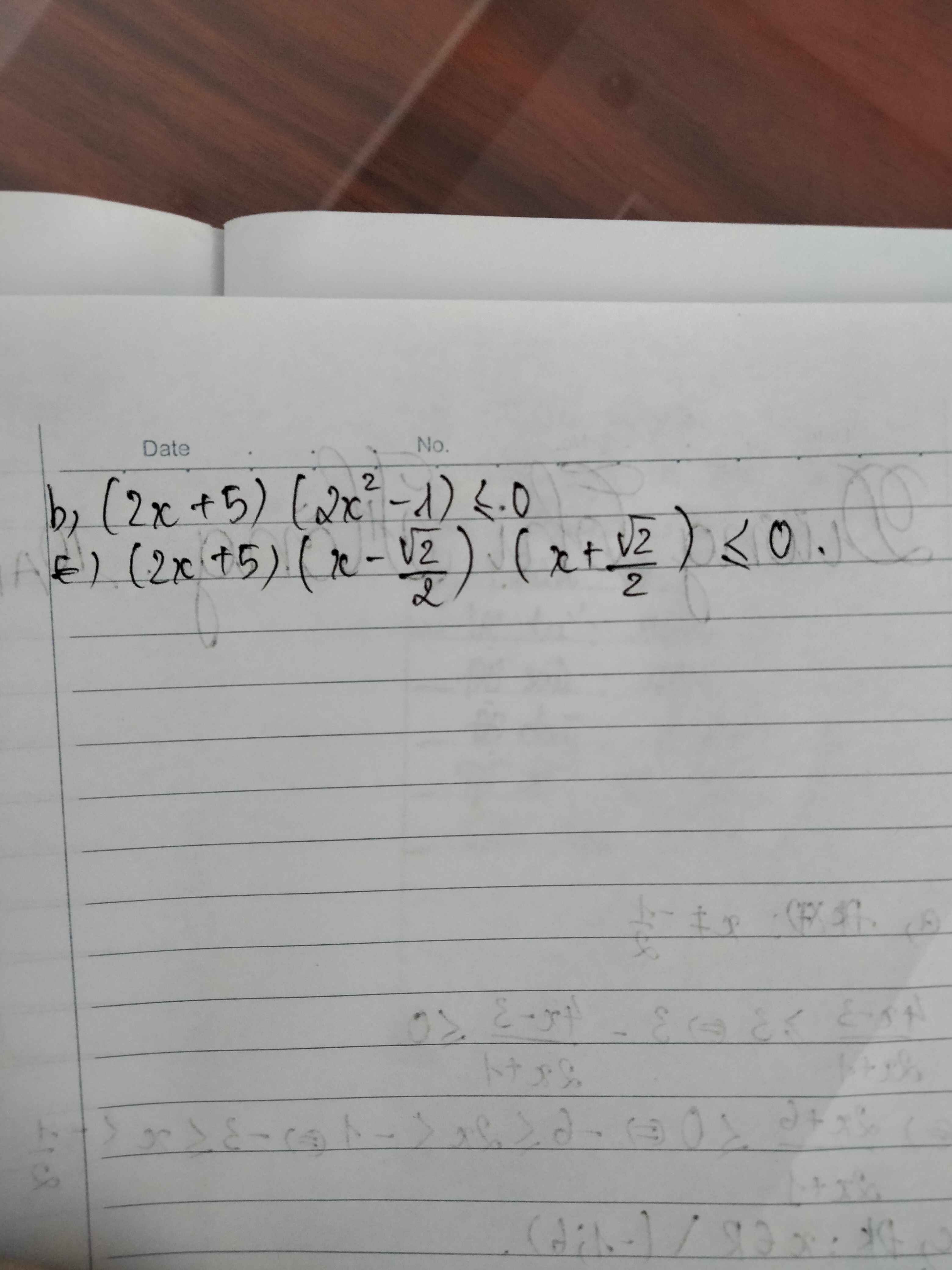
Giải bất phương trình (x-1).(x+3) <0
**Lưu ý: làm cách thông thường, không phải lập bảng xét dấu các bạn nhé. Kết quả sau khi mình làm bằng cách lập bảng xét dấu là -3<x<1
Xe máy thứ nhất 1 giờ đi được 1/4 quảng đường
Xe máy thứ hai 1 giờ đi được 1/3 quảng đường
Sau 1,5 giờ 2 xe đi được:(1/4+1/3)x1,5=7/12x3/2=7/8(quảng đường)
quảng đường AB là:
15x8=120(km)
Xem lại đề đi bạnn
Trả lời đúng giúp mình.
a) Lập bảng xét dấu của tam thức bậc hai \(f\left( x \right) = {x^2} - x - 2\)
b) Giải bất phương trình \({x^2} - x - 2 > 0\)
Tham khảo:
a) Ta có tam thức bậc hai \(f\left( x \right) = {x^2} - x - 2\) có 2 nghiệm phân biệt \({x_1} = - 1,{x_2} = 2\) và hệ số \(a = 1 > 0\)
Ta có bảng xét dấu f(x) như sau:

Vậy tập nghiệm của bất phương trình là \(\left( { - \infty ; - 1} \right) \cup \left( {2; + \infty } \right)\)b) Từ bảng xét dấu ta thấy \(f\left( x \right) > 0 \Leftrightarrow \left[ \begin{array}{l}x < - 1\\x > 2\end{array} \right.\)
cái này xét dấu = ntn v ạ?
Giải bất phương trình sau bằng cách lập bảng xét dấu \(\frac{5-2x}{x+2}\ge3\)
Lập bảng xét dấu để làm gì? Nêu ý nghĩa của bảng xét dấu trong phương trình chưa trị tuyệt đối
$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$
#$$%#^&*(*(*&$$#^&*((*&^&)*%#!@@%^^%
Giải bằng cách kẻ bảng xét dấu dùm em với ạ 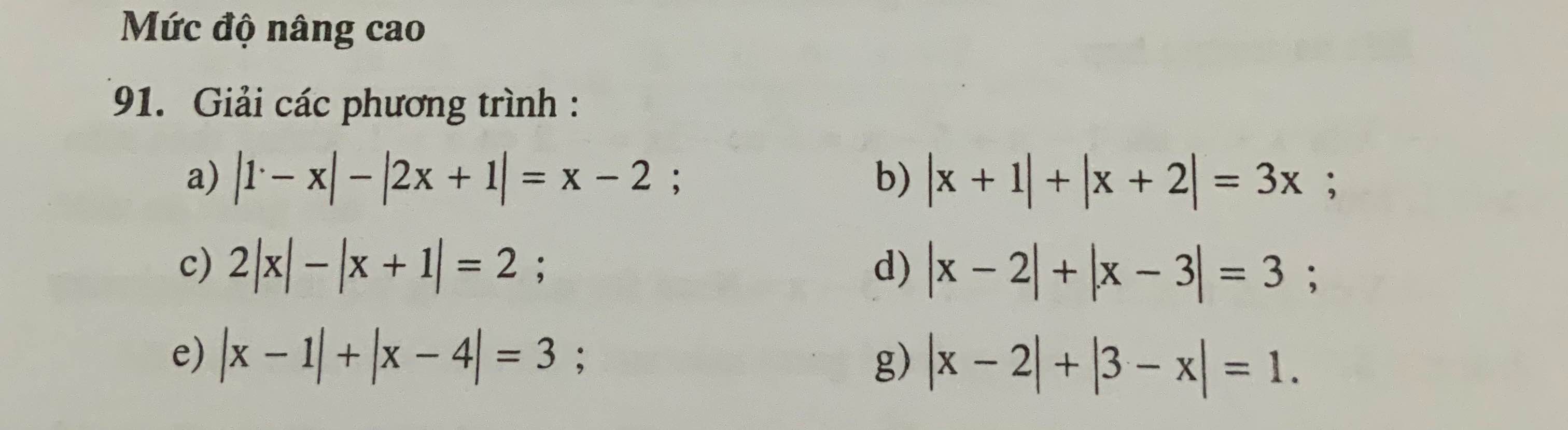
a: |1-x|-|2x+1|=x-2
=>|x-1|-|2x+1|=x-2(1)
TH1: x<-1/2
Phương trình (1) sẽ tương đương với:
1-x-(-2x-1)=x-2
=>1-x+2x+1=x-2
=>x+2=x-2
=>2=-2(vô lý)
=>\(x\in\varnothing\)
TH2: \(-\dfrac{1}{2}< =x< 1\)
Phương trình (1) sẽ trở thành:
\(1-x-\left(2x+1\right)=x-2\)
=>1-x-2x-1=x-2
=>-3x=x-2
=>-4x=-2
=>\(x=\dfrac{1}{2}\left(nhận\right)\)
TH3: x>=1
Phương trình (1) sẽ trở thành:
\(x-1-\left(2x+1\right)=x-2\)
=>x-1-2x-1=x-2
=>-x-2=x-2
=>-2x=0
=>x=0(loại)
b: \(\left|x+1\right|+\left|x+2\right|=3x\left(2\right)\)
TH1: x<-2
Phương trình (2) sẽ trở thành:
-x-1+(-x-2)=3x
=>\(3x=-2x-3\)
=>\(5x=-3\)
=>\(x=-\dfrac{3}{5}\left(loại\right)\)
TH2: -2<=x<-1
Phương trình (2) sẽ trở thành:
\(-x-1+x+2=3x\)
=>3x=1
=>\(x=\dfrac{1}{3}\left(loại\right)\)
TH3: x>=-1
Phương trình (2) sẽ trở thành:
\(x+1+x+2=3x\)
=>3x=2x+3
=>x=3(nhận)
c: \(2\left|x\right|-\left|x+1\right|=2\left(3\right)\)
TH1: x<-1
Phương trình (3) sẽ trở thành:
-2x-(-x-1)=2
=>-2x+x+1=2
=>-x+1=2
=>-x=1
=>x=-1(loại)
TH2: -1<=x<0
Phương trình (3) sẽ trở thành:
\(-2x-\left(x+1\right)=2\)
=>-2x-x-1=2
=>-3x=3
=>x=-1(nhận)
TH3: x>=0
Phương trình (3) sẽ trở thành:
\(2x-\left(x+1\right)=2\)
=>x-1=2
=>x=3(nhận)
d: \(\left|x-2\right|+\left|x-3\right|=3\left(4\right)\)
TH1: x<2
Phương trình (4) sẽ trở thành:
2-x+3-x=3
=>5-2x=3
=>2x=2
=>x=1(nhận)
Th2: 2<=x<3
Phương trình (4) sẽ trở thành:
\(x-2+3-x=3\)
=>1=3(loại)
Th3: x>=3
Phương trình (4) sẽ trở thành:
x-2+x-3=3
=>2x-5=3
=>2x=8
=>x=4(nhận)
e: |x-1|+|x-4|=3(5)
TH1: x<1
Phương trình (5) sẽ trở thành:
1-x+4-x=3
=>5-2x=3
=>2x=2
=>x=1(loại)
TH2: 1<=x<4
Phương trình (5) sẽ trở thành:
x-1+4-x=3
=>3=3(luôn đúng)
TH3: x>=4
Phương trình (5) sẽ trở thành:
x-1+x-4=3
=>2x-5=3
=>2x=8
=>x=4(nhận)
g: |x-2|+|3-x|=1
=>|x-2|+|x-3|=1(6)
TH1: x<2
Phương trình (6) sẽ trở thành:
2-x+3-x=1
=>5-2x=1
=>2x=4
=>x=2(loại)
TH2: 2<=x<3
Phương trình (6) sẽ trở thành:
x-2+3-x=1
=>1=1(luôn đúng)
TH3: x>=3
Phương trình (6) sẽ trở thành:
x-2+x-3=1
=>2x-5=1
=>2x=6
=>x=3(nhận)
cách lập bảng xét dấu mang giá trị tuyệt đối
vd:hãy lập bảng xét dấu:
\(\left|x-3\right|-\left|x+3\right|\)
Của bạn thiếu dấu bằng .
Ta xét dấu các biểu thức trong dấu GTTĐ để khử dấu gttđ
VD1: Giải pt:
|2x−1|+|2x−5|=4−−(1)|2x−1|+|2x−5|=4−−(1)
Giải:
Ta lập bảng khử dấu gttđ: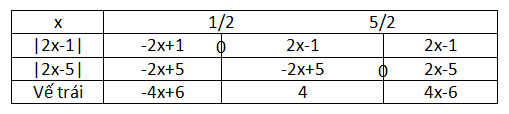
Từ đó ta xét 3 trường hợp sau:
- Xét x<12x<12
(1) trở thành −4x+6=4⇔x<12−4x+6=4⇔x<12, không phụ thuộc vào khoảng đang xét
- Xét 12≤x<5212≤x<52, (1) trở thành 4=44=4 đúng với mọi x khoảng đang xét
- Xét x≥52x≥52:
(1) trở thành 4x−6=4⇔x=524x−6=4⇔x=52, thuộc vào khoảng đang xét
Kết luận: Nghiệm của pt (1) là 12≤x≤5212≤x≤52
Mách nhỏ: Để khỏi nhầm lẫn trong việc lập bảng khử dấu giá trị tuyệt đối, các bạn hãy nhớ lấy câu: "Trái khác, phải cùng" tức là: Bên trái nghiệm của biểu thức sẽ mang dấu khác (trái) với biếu thức ta nhìn thấy, bên phải nghiệm của biểu thức sẽ mang dấu cùng với biểu thức ta nhìn thấy.
Phương pháp 2: Phương pháp biến đổi tương đương
Ta áp dụng 2 phép biến đổi cơ bản sau:
1) |a|=b⇔⎧⎪⎨⎪⎩b≥0[a=ba=−b|a|=b⇔{b≥0[a=ba=−b
2) |a|=|b|⇔[a=ba=−b|a|=|b|⇔[a=ba=−b
VD: Giải pt:
|x−1|=|3x−5|−(2)|x−1|=|3x−5|−(2)
Giải:
Áp dụng phép biến đổi 2 ta có:
(2)⇔[x−1=3x−5x−1=−3x+5(2)⇔[x−1=3x−5x−1=−3x+5
⇔⎡⎣x=2x=32⇔[x=2x=32
Kết luận: pt (2) có 2 nghiệm x1=2;x2=32x1=2;x2=32
Nhận xét: Ta có thể sử dụng phương pháp 1 để giải phương trình (2)