cho tam giác ABC trực tâm H , AH=7. BH=căn 5, CH=17 tính đường cao AD và diện tích tam giác ABC
Cho tam giác ABC vuông tại A vẽ đường cao AH chia cạnh huyền BC thành hai đoạn thẳng BH=20cm và CH=45cm
a)Chứng minh tam giác HBA đồng dạng với tam giác HAC
b)Tính độ dài AH
c)Tính diện tích tam giác ABC
d)Cho AB=10 căn 3 ,AC=15 căn 3 .Gọi AD là đường phân giác trong của góc A và AH là đường cao .Tính tỉ số diện tích của tam giác ABC và tam giác ACD
Cho tam giác ABC vuông tại A, đcao AH. Biết CH - BH = 3(cm) và AB = căn 5 (cm). Tính BH, CH, AH, AC và diện tích tam giác ABC???
Cho tam giác ABC vuông tại A đường cao AH(H € BC) biết BH=9cm CH=16cm. Tính độ dài và diện tích tam giác ABC
\(S_{ABC}=\dfrac{AH\cdot BC}{2}=150\left(cm^2\right)\)
Cho tam giác ABC vuông tại A đường cao AH(H € BC) biết BH=9cm CH=16cm. Tính độ dài và diện tích tam giác ABC
\(S_{BAC}=\dfrac{AH\cdot BC}{2}=\dfrac{12\cdot25}{2}=150\left(cm^2\right)\)
Cho tam giác ABC vuông tại A, đường cao AH. Biết BH= 4cm, CH= 9cm.
a) Tính độ dài đường cao AH và A B C ⏜ của tam giác ABC.
b) Vẽ đường trung tuyến AM M ∈ B C của tam giác ABC, tính AM và diện tích tam giác AHM

a , Δ A B C , A ⏜ = 90 0 , A H ⊥ B C g t ⇒ A H = B H . C H = 4.9 = 6 c m Δ A B H , H ⏜ = 90 0 g t ⇒ tan B = A H B H = 6 4 ⇒ B ⏜ ≈ 56 , 3 0 b , Δ A B C , A ⏜ = 90 0 , M B = M C g t ⇒ A M = 1 2 B C = 1 2 .13 = 6 , 5 c m S Δ A H M = 1 2 M H . A H = 1 2 .2 , 5.6 = 7 , 5 c m 2
Bài 1: Cho tam giác ABC vuông tại A, đường cao AH = 5cm. Biết CH = 6cm. tính:
a) AB, AC,BC và BH?
b) Diện tích tam giác ABC
Bài2: Cho tam giác ABC vuông tại A, đường cao AH; AB = 15cm; BC = 25cm. BTính:
a) AC,AH, HC và BH?
b) Diện tích tam giác ABC
\(1,\)
\(a,\) Áp dụng HTL tam giác
\(\left\{{}\begin{matrix}AH^2=CH\cdot BH\\AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}BH=\dfrac{AH^2}{CH}=\dfrac{25}{6}\left(cm\right)\\AB=\sqrt{\dfrac{25}{6}\left(\dfrac{25}{6}+6\right)}=\dfrac{5\sqrt{61}}{6}\left(cm\right)\\AC=\sqrt{6\left(\dfrac{25}{6}+6\right)}=\sqrt{61}\left(cm\right)\end{matrix}\right.\\ BC=\dfrac{25}{6}+6=\dfrac{61}{6}\left(cm\right)\)
\(b,S_{ABC}=\dfrac{1}{2}AH\cdot BC=\dfrac{1}{2}\cdot5\cdot\dfrac{61}{6}=\dfrac{305}{12}\left(cm^2\right)\)
Gọi H là trực tâm tam giác ABC; phương trình của các cạnh và đường cao tam giác là:
AB: 7x – y+ 4= 0 và BH: 2x+ y- 4= 0; AH: x - y -2= 0
Phương trình đường cao CH của tam giác ABC là:
A. 7x- y+ 2= 0
B. 7x+y-2= 0
C. x+ 7y + 2= 0
D. x+ 7y-2= 0
Hai đường thẳng AH và BH cắt nhau tại H nên tọa đô của H là nghiệm hệ
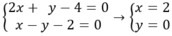
Vậy H( 2; 0)
Do CH vuông góc với AB mà AB: 7x – y + 4= 0 nên CH có
![]()
Suy ra; phương trình CH:
1(x-2) + 7( y-0) = 0
Hay x+ 7y -2= 0
Chọn D.
Cho tam giác ABC cân tại A , đường cao AD , trực tâm H, biết rằng góc BAC <90 độ . AH=14cm; BH=HC =30cm. Tính AD=?
Cho Tam giác ABC nhọn đường cao AD (à thuộc BC. Gọi H là điểm thuộc đoạn AD sao cho DA.DH=DB.DC BH cắt CA tại E, CH cắt AB tại F. Chứng minh rằng: 1. Hai tam giác DAB, DCH đồng dạng và H là trực tâm của Tam giác ABC 2. AE.AC=AH.AD=AF.AB 3. AH.AD+BH.BE+CH.CF=AB^2+BC^2+AC^2/2 Giúp mình câu 3 với ạ mình cảm ơn
3:
Xét ΔCEH vuông tại E và ΔCFA vuông tại F có
\(\widehat{FCA}\) chung
Do đó: ΔCEH đồng dạng với ΔCFA
=>CE/CF=CH/CA
=>\(CE\cdot CA=CH\cdot CF\)
Xét ΔCDH vuông tại D và ΔCFB vuông tại F có
\(\widehat{FCB}\) chung
Do đó: ΔCDH đồng dạng với ΔCFB
=>CD/CF=CH/CB
=>CD*CB=CH*CF
=>CD*CB=CH*CF=CE*CA
Xét ΔBDH vuông tại D và ΔBEC vuông tại E có
\(\widehat{EBC}\) chung
Do đó: ΔBDH đồng dạng với ΔBEC
=>BD/BE=BH/BC
=>\(BD\cdot BC=BH\cdot BE\)
Xét ΔBDA vuông tại D và ΔBFC vuông tại F có
góc DBA chung
Do đó: ΔBDA đồng dạng với ΔBFC
=>BD/BF=BA/BC
=>BD*BC=BF*BA
=>BD*BC=BF*BA=BH*BE
\(AH\cdot AD+BH\cdot BE=AF\cdot AB+BF\cdot BA=BA^2\)
\(AH\cdot AD+CH\cdot CF=AE\cdot AC+CE\cdot CA=AC^2\)
\(BH\cdot BE+CH\cdot CF=BD\cdot BC+CD\cdot CB=BC^2\)
Do đó: \(2\left(AH\cdot AD+BH\cdot BE+CH\cdot CF\right)=BA^2+AC^2+BC^2\)
=>\(AH\cdot AD+BH\cdot BE+CH\cdot CF=\dfrac{AB^2+AC^2+BC^2}{2}\)