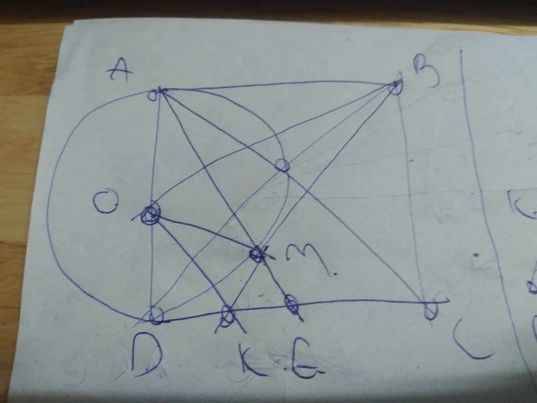
Vẽ Hình: Cho đường tròn ( O ; R ) và điểm A nằm ngoài đường tròn ( O ). Từ A kẻ 2 tiếp tuyến AE, AH đến đường tròn ( O ) ( E, H là các tiếp điểm ). EH cắt AO tại M. Kẻ đường kính KH. I là trung điểm của EK. Tia AE cắt tia OI tại B
KT
Những câu hỏi liên quan
Cho hình vẽ bên có hai đường tròn (O; 3cm) và (
O
1
; 3cm). Điểm
O
1
nằm trên đường tròn tâm O.a) Vẽ đường tròn tâm A, bán kính 3cm.b) Vì sao đường tròn (A; 3cm) đi qua O và
O
1
?
Đọc tiếp
Cho hình vẽ bên có hai đường tròn (O; 3cm) và ( O 1 ; 3cm). Điểm O 1 nằm trên đường tròn tâm O.
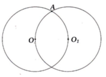
a) Vẽ đường tròn tâm A, bán kính 3cm.
b) Vì sao đường tròn (A; 3cm) đi qua O và O 1 ?
a) HS tự vẽ hình.
b) Đường tròn (A; 3cm) đi qua O và O1 vì OA = O 1 A = 3 cm.
Đúng 0
Bình luận (0)
Cho hình vẽ bên có hai đường tròn (O; 3cm) và (
O
1
; 3cm). Điểm
O
1
nằm trên đường tròn tâm O.a) Vẽ đường tròn tâm A, bán kính 3cm.b) Vì sao đường tròn (A; 3cm) đi qua O và
O
1
?
Đọc tiếp
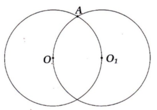
Cho hình vẽ bên có hai đường tròn (O; 3cm) và ( O 1 ; 3cm). Điểm O 1 nằm trên đường tròn tâm O.
a) Vẽ đường tròn tâm A, bán kính 3cm.
b) Vì sao đường tròn (A; 3cm) đi qua O và O 1 ?
a) HS tự vẽ hình.
b) Đường tròn (A; 3cm) đi qua O và O 1 vì O A = O 1 A = 3 c m .
Đúng 0
Bình luận (0)
a) Vẽ đường tròn tâm O, bán kính 2cm.
b) Vẽ hình vuông nội tiếp đường tròn (O) ở câu a).
c) Tính bán kính r của đường tròn nội tiếp hình vuông ở câu b) rồi vẽ đường tròn (O; r).
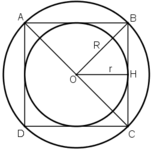
a) Chọn điểm O là tâm, mở compa có độ dài 2cm vẽ đường tròn tâm O, bán kính 2cm.
b) Vẽ đường kính AC và BD vuông góc với nhau. Nối A với B, B với C, C với D, D với A ta được tứ giác ABCD là hình vuông nội tiếp đường tròn (O; 2cm).
c) Vẽ OH ⊥ BC.
⇒ OH là khoảng cách từ từ tâm O đến BC
Vì AB = BC = CD = DA ( ABCD là hình vuông) nên khoảng cách từ tâm O đến AB, BC, CD, DA bằng nhau ( định lý lien hệ giữa dây cung và khoảng cách từ tâm đến dây)
⇒ O là tâm đường tròn nội tiếp hình vuông ABCD
OH là bán kính r của đường tròn nội tiếp hình vuông ABCD.
Tam giác vuông OBC có OH là đường trung tuyến ⇒ 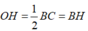
Xét tam giác vuông OHB có: r 2 + r 2 = O B 2 = 2 2 ⇒ 2 r 2 = 4 ⇒ r 2 = 2 ⇒ r = 2 ( cm )
Vẽ đường tròn (O; OH). Đường tròn này nội tiếp hình vuông, tiếp xúc bốn cạnh hình vuông tại các trung điểm của mỗi cạnh.
Kiến thức áp dụng
+ Đường tròn ngoại tiếp đa giác nếu đường tròn đó đi qua tất cả các đỉnh của đa giác. Khi đó ta nói đa giác nội tiếp đường tròn.
+ Đường tròn nội tiếp đa giác là đường tròn tiếp xúc với tất cả các cạnh của đa giác. Khi đó ta nói đa giác ngoại tiếp đường tròn.
Đúng 0
Bình luận (0)
vẽ hình hộ mình đề này Cho hình vuông ABCD có độ dài cạnh bằng 4cm. Vẽ đường tròn tâm O đường kính AD, kẻ BM là tiếp tuyến của đường tròn O ( M là tiếp điểm, M khác A), BM cắt CD tại K a) Cm 4 điểm A,B,M,O cùng thuộc 1 đg tròn ( cm: 2 tam nội tiếp) b) Chứng minh OB vuông góc OK và BM.MK A...
Đọc tiếp
vẽ hình hộ mình đề này Cho hình vuông ABCD có độ dài cạnh bằng 4cm. Vẽ đường tròn tâm O đường kính AD, kẻ BM là tiếp tuyến của đường tròn O ( M là tiếp điểm, M khác A), BM cắt CD tại K a) Cm 4 điểm A,B,M,O cùng thuộc 1 đg tròn ( cm: 2 tam nội tiếp) b) Chứng minh OB vuông góc OK và BM.MK= AB^2/4 c) Đường thẳng AM cắt CD tại E. Cm K là trung điểm của ED và tính chu vi tứ giác ABKD
Cho đường tròn tâm O đường kính AB. Vẽ đường tròn tâm I đg kính OA bán kính OC của đg tròn tâm O cắt đg trong tâm I tại D. Vẽ CH vuong goc AB (C thuộc đg tròn tâm O, đg kính AB). C/m rằng ACDH là hình thang cân. Vẽ hình giúp e với luôn đk ạ
Xét (I) có
ΔADO nội tiếp
AO là đường kính
=>ΔADO vuông tại D
góc ADC=góc AHC=90 độ
=>AHDC nội tiếp
Xét ΔOHC vuông tại H và ΔODA vuông tại D có
OC=OA
góc HOC chung
=>ΔOHC=ΔODA
=>OH=OD
Xét ΔOAC có OH/OA=OD/OC
nên HD//AC
Xét tứ giác AHDC có
HD//AC
góc HAC=góc DCA
=>AHDC là hình thang cân
Đúng 0
Bình luận (0)
cho hai đường tròn (M;15) và (N;15) cùng tiếp xúc ngoài với đường tròn (O;15) sao cho O nằm giữa M và N. Tia đối của tia MO cắt đường tròn (M) tại A. vẽ dây AC của đường tròn (M) sao cho AC=12\(\sqrt{6}\)
AI VẼ HỘ MIK HÌNH VỚI HÌNH DẢK
QUÁ COMBA MIK KO ĐỦ 15cm =))
TOÁN HÌNH LỚP 9:
Cho đường tròn tâm O đường kính AB. Vẽ đường tròn tâm I đường kính OA. Bán kính OC của đường tròn O cắt đường tròn ( I ) tại D. Vẽ CH vuông góc với AB. Chứng minh : ACDH là hình thang cân.
cho đường tròn (O) qua điểm M ở ngoài đường tròn (O) vẽ tiếp tuyến MC với đường tròn (O) (C là tiếp điểm )vẽ dây CD của đường mtronf (O) vuông góc với MO tại I 1) chứng minh :om là đường trung trực của đoạn thẳng CD
mọi người vẽ hình giúp em với ạ em cảm ơn

Ta có: ΔOCD cân tại O
mà OM là đường cao(OM\(\perp\)CD tại I)
nên OM là trung trực của CD
Đúng 0
Bình luận (0)
a) Vẽ đường tròn tâm O, bán kính 2cm.
b) Vẽ hình vuông nội tiếp đường tròn (O) ở câu a.
c) Tính bán kính r của đường tròn nội tiếp hình vuông ở câu b) rồi vẽ đường tròn (O; r).
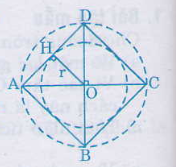
a) Chọn điểm O làm tâm , mở compa có độ dài 2cm vẽ đường tròn tâm O, bán kính 2cm: (O; 2cm)
Vẽ bằng eke và thước thẳng.
b) Vẽ đường kính AC và BD vuông góc với nhau. Nối A với B, B với C, C với D, D với A ta được tứ giác ABCD là hình vuông nội tiếp đường tròn (O;2cm)
c) Vẽ OH ⊥ AD
OH là bán kính r của đường tròn nội tiếp hình vuông ABCD.
r = OH = AH.
r2 + r2 = OA2 = 22 => 2r2 = 4 => r = √2 (cm)
Vẽ đường tròn (O;√2cm). Đường tròn này nội tiếp hình vuông, tiếp xúc bốn cạnh hình vuông tại các trung điểm của mỗi cạnh
Đúng 0
Bình luận (0)
Cho đường tròn tâm O,bán kính 1,5cm.Hãy vẽ hình vuông ABCD có bốn đỉnh nằm trên đường tròn đó. Nêu cách vẽ
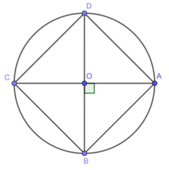
*Cách vẽ:
- Vẽ đường tròn tâm O bán kính 1,5cm
- Vẽ hai đường kính AC và BD vuông góc với nhau
- Nối AB, BC , CD, DA lại với nhau ta được hình vuông ABCD nội tiếp trong đường tròn (O; 1,5)
*Chứng minh:
Ta có : OA = OC , OB =OD
Suy ra ABCD là hình bình hành
Mặt khác : AC = BD và AC ⊥ BD
Suy ra ABCD là hình vuông
Đúng 0
Bình luận (0)