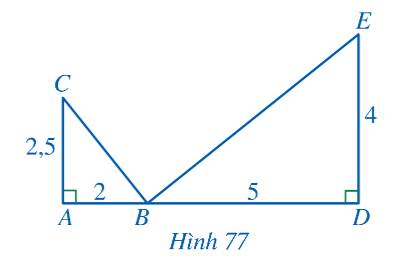
Cho Hình 77, chứng minh
a) \(\widehat {ABC} = \widehat {BED}\)
b) \(BC \bot BE\)
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
Cho hình chóp O.ABC có \(\widehat {AOB} = \widehat {BOC} = \widehat {COA} = 90^\circ \). Chứng minh rằng:
a) \(BC \bot OA\)
b) \(CA \bot OB\)
c) \(AB \bot OC\)
a) Ta có: \(\left. \begin{array}{l}OA \bot OB\\OA \bot OC\end{array} \right\} \Rightarrow OA \bot \left( {OBC} \right)\)
Mà \(BC \in \left( {OBC} \right) \Rightarrow OA \bot BC\)
b) Ta có \(\left. \begin{array}{l}OA \bot OB\\OB \bot OC\end{array} \right\} \Rightarrow OB \bot \left( {OAC} \right)\)
Mà \(CA \in \left( {OAC} \right) \Rightarrow CA \bot OB\)
c) Ta có \(\left. \begin{array}{l}OC \bot OB\\OA \bot OC\end{array} \right\} \Rightarrow OC \bot \left( {OAB} \right)\)
Mà \(AB \in \left( {OAB} \right) \Rightarrow AB \bot OC\)
d,Ta có : \(BE\bot AC (gt);DF\bot AC(gt)=> BE \) song song với DF
Chứng minh : \(\bigtriangleup{BEO}\) đồng dạng \(\bigtriangleup{DFO} (g-c-g)\)
=> BE = DF
=> Tứ giác BEDF là hình bình hành
e, Ta có \(\widehat{ABC}=\widehat{ADC}=>\widehat{HBC}=\widehat{KDC}\)
Chứng minh : \(\bigtriangleup{CBH} \) đồng dạng \(\bigtriangleup{CDK} (g-g) \)
=> \(\dfrac{CH}{CB}.\dfrac{CK}{CD}=> CH.CD=CK.CB\)
f, Chứng minh : \(\bigtriangleup{AFD} \) đồng dạng \(\bigtriangleup{AKC} (g-g)\)
=> \(\dfrac{AF}{AD}=\dfrac{AK}{AC}=> AD.AK=AF.AC\)
Chứng minh : \(\bigtriangleup{CFD} \) đồng dạng \(\bigtriangleup{AHC} (g-g)\)
=> \(\dfrac{CF}{CD}=\dfrac{AH}{AC}\)
Mà CD = AB => \(\dfrac{CF}{AB}=\dfrac{AH}{AC}=> AB.AH=CF.AC\)
=> \(=> AB.AH+AD.AK=CF.AC+AF.AC=(CF+AF).AC=AC^2\)
Cho hình chóp \(S.ABC\) có \(SA = SB = SC = a,\widehat {BSA} = \widehat {CSA} = {60^ \circ },\) \(\widehat {BSC} = {90^ \circ }\). Cho \(I\) và \(J\) lần lượt là trung điểm của \(SA\) và \(BC\). Chứng minh rằng \(IJ \bot SA\) và \(IJ \bot BC\).

\(\Delta SAB,\Delta SAC\) đều \( \Rightarrow AB = {\rm{A}}C = a\)
\(BC = \sqrt {S{B^2} + S{C^2}} = a\sqrt 2 \)
\( \Rightarrow \Delta ABC\) vuông cân tại \(A\)
\(AJ\) là trung tuyến của tam giác \(ABC\)\( \Rightarrow AJ = \frac{1}{2}BC = \frac{{a\sqrt 2 }}{2}\)
\(\Delta SBC\) vuông cân tại \(S\) có \(SJ\) là trung tuyến
\( \Rightarrow SJ = \frac{1}{2}BC = \frac{{a\sqrt 2 }}{2}\)
\(IJ\) là trung tuyến của tam giác \(SAJ\)\( \Rightarrow IJ = \frac{{\sqrt {2\left( {A{J^2} + S{J^2}} \right) - S{A^2}} }}{2} = \frac{a}{2}\)
\(AI = \frac{1}{2}SA = \frac{a}{2};BJ = \frac{1}{2}BC = \frac{a}{2}\)
Xét tam giác \(AIJ\) có: \(A{I^2} + I{J^2} = A{J^2}\)
\( \Rightarrow \Delta AIJ\) vuông tại \(I\)\( \Rightarrow AI \bot IJ \Rightarrow SA \bot IJ\)
\(\Delta SAB\) đều \( \Rightarrow BI = \sqrt {A{B^2} - A{I^2}} = \frac{{a\sqrt 3 }}{2}\)
Xét tam giác \(BIJ\) có: \(B{J^2} + I{J^2} = B{I^2}\)
\( \Rightarrow \Delta BIJ\) vuông tại \(J\)\( \Rightarrow BJ \bot IJ \Rightarrow BC \bot IJ\)
Cho tam giác ABC. Đường trung trực của hai cạnh AB và AC cắt nhau tại điểm O nằm trong tam giác. M là trung điểm của BC. Chứng minh:
a) \(OM \bot BC\);
b) \(\widehat {MOB} = \widehat {MOC}\).
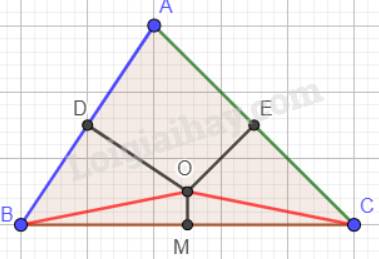
a) Ta có: đường trung trực của hai cạnh AB và AC cắt nhau tại O và O nằm trong tam giác. Nên O là giao điểm của ba đường trung trực của tam giác ABC.
Mà M là trung điểm của cạnh BC nên OM là đường trung trực của đoạn thẳng BC hay \(OM \bot BC\).
b) Ta có: Giao của ba đường trung trực trong tam giác thì cách đều ba đỉnh của tam giác đó.
Hay OB = OC nên tam giác OBC cân tại O. Suy ra: \(\widehat {OBC} = \widehat {OCB}\) hay \(\widehat {OBM} = \widehat {OCM}\). ( tính chất tam giác cân)
Xét tam giác OMB và tam giác OMC có:
OB = OC;
\(\widehat {OBM} = \widehat {OCM}\);
MB = MC (M là trung điểm của đoạn thẳng BC).
Vậy \(\Delta OMB = \Delta OMC\)(c.g.c)
Do đó,\(\widehat {MOB} = \widehat {MOC}\) ( 2 góc tương ứng).
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại \(B,BC = \) a và \(\widehat {CAB} = {30^0}\). Biết \(SA \bot (ABC)\) và \(SA = a\sqrt 2 \).
a) Chứng minh rằng \((SBC) \bot (SAB)\).
b) Tính theo a khoảng cách từ điểm \(A\) đến đường thẳng SC và khoảng cách từ điểm \(A\) đến mặt phẳng \((SBC)\).
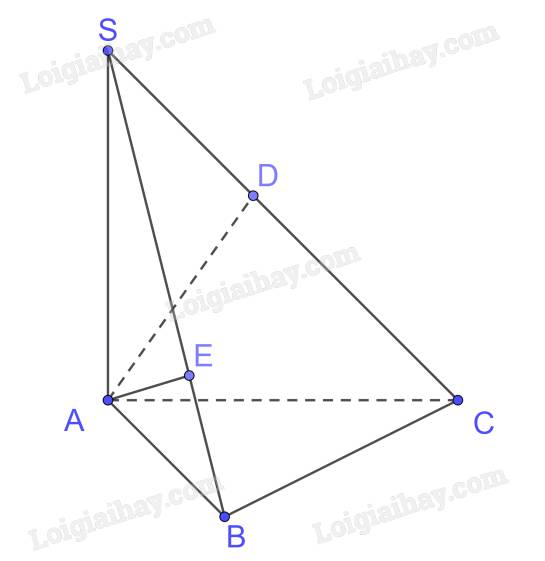
a) \(SA \bot BC\left( {SA \bot \left( {ABC} \right)} \right),AB \bot BC \Rightarrow BC \bot \left( {SAB} \right),BC \subset \left( {SBC} \right) \Rightarrow \left( {SBC} \right) \bot \left( {SAB} \right)\)
b) +) Trong (SAC) kẻ \(AD \bot SC \Rightarrow d\left( {A,SC} \right) = AD\)
Xét tam giác ABC vuông tại B có
\(\sin \widehat {CAB} = \frac{{BC}}{{AC}} \Rightarrow AC = \frac{a}{{\sin {{30}^0}}} = 2a\)
Xét tam giác SAC vuông tại A có
\(\frac{1}{{A{D^2}}} = \frac{1}{{S{A^2}}} + \frac{1}{{A{C^2}}} = \frac{1}{{{{\left( {a\sqrt 2 } \right)}^2}}} + \frac{1}{{{{\left( {2a} \right)}^2}}} = \frac{3}{{4{a^2}}} \Rightarrow AD = \frac{{2a\sqrt 3 }}{3}\)
Do đó \(d\left( {A,SC} \right) = \frac{{2a\sqrt 3 }}{3}\)
+) \(\left( {SAB} \right) \bot \left( {SBC} \right),\left( {SAB} \right) \cap \left( {SBC} \right) = SB\)
Trong (SAB) kẻ \(AE \bot SB\)
\( \Rightarrow AE \bot \left( {SBC} \right) \Rightarrow d\left( {A,\left( {SBC} \right)} \right) = AE\)
Xét tam giác ABC vuông tại B có
\(\tan \widehat {CAB} = \frac{{BC}}{{AB}} \Rightarrow AB = \frac{a}{{\tan {{30}^0}}} = a\sqrt 3 \)
Xét tam giác SAB vuông tại A có
\(\frac{1}{{A{E^2}}} = \frac{1}{{S{A^2}}} + \frac{1}{{A{B^2}}} = \frac{1}{{{{\left( {a\sqrt 2 } \right)}^2}}} + \frac{1}{{{{\left( {a\sqrt 3 } \right)}^2}}} = \frac{5}{{6{a^2}}} \Rightarrow AE = \frac{{a\sqrt {30} }}{5}\)
Vậy \(d\left( {A,\left( {SBC} \right)} \right) = \frac{{a\sqrt {30} }}{5}\)
Cho hình chóp S.ABC có SA \( \bot \) (ABC), AB = AC = a, \(\widehat {BAC} = {120^0},SA = \frac{a}{{2\sqrt 3 }}.\) Gọi M là trung điểm của BC.
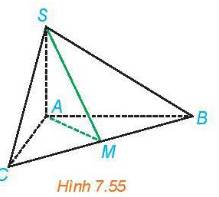
a) Chứng minh rằng \(\widehat {SMA}\) là một góc phẳng của góc nhị diện \(S, BC, A].
b) Tính số đo của góc nhị diện \(S, BC, A].
a) Xét tam giác ABC có AB = AC => tam giác ABC cân tại A mà M là trung điểm BC
=> \(AM \bot BC\) (1)
\(\begin{array}{l}SA \bot BC\left( {SA \bot \left( {ABCD} \right)} \right)\\ \Rightarrow BC \bot \left( {SAM} \right);SM \subset \left( {SAM} \right) \Rightarrow BC \bot SM\,\,\,\left( 2 \right)\end{array}\)
Từ (1), (2) ta có \(\widehat {SMA}\) là một góc phẳng của góc nhị diện [S, BC, A].
b) Xét tam giác ABC cân tại A có
\(\widehat {BAC} = {120^0} \Rightarrow \widehat {ACB} = {30^0}\)
\(\sin \widehat {ACB} = \frac{{AM}}{{AC}} \Leftrightarrow \tan {30^0} = \frac{{AM}}{a} \Leftrightarrow AM = \frac{a}{{\sqrt 3 }}\)
\(\tan \widehat {SMA} = \frac{{SA}}{{AM}} = \frac{a}{{2\sqrt 3 }}:\frac{a}{{\sqrt 3 }} = \frac{1}{2} \Rightarrow \widehat {SMA} = \arctan \frac{1}{2}\)
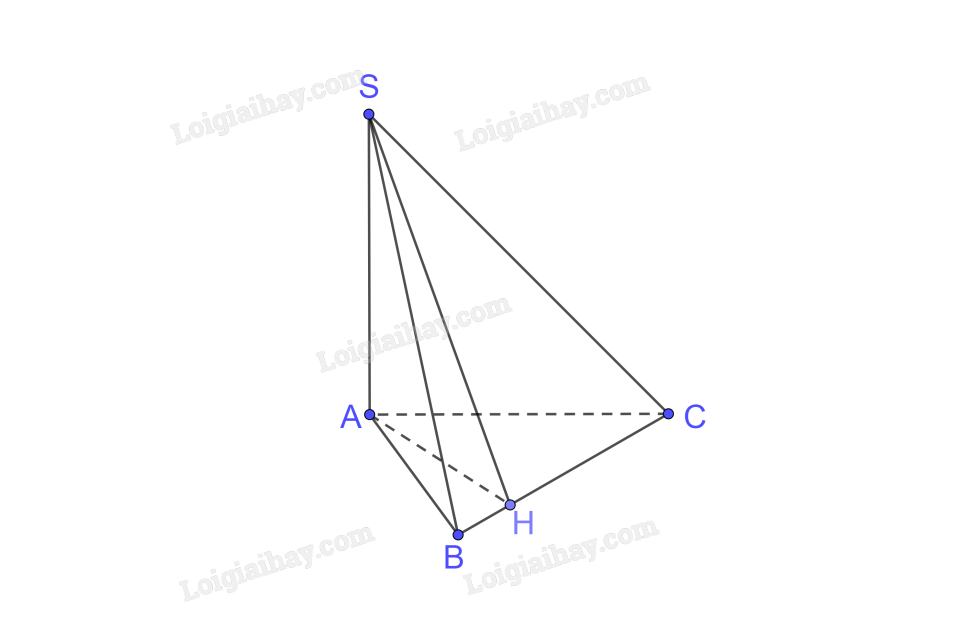
Cho hình chóp S.ABC có SA \( \bot \) (ABC). Gọi H là hình chiếu của A trên BC.
a) Chứng minh rằng (SAB) \( \bot \) (ABC) và (SAH) \( \bot \) (SBC).
b) Giả sử tam giác ABC vuông tại A, \(\widehat {ABC} = {30^0},AC = a,SA = \frac{{a\sqrt 3 }}{2}.\) Tính số đo của góc nhị diện [S, BC, A]
a) \(SA \bot \left( {ABC} \right);SA \subset \left( {SAB} \right) \Rightarrow \left( {SAB} \right) \bot \left( {ABC} \right)\)
\(\left. \begin{array}{l}AH \bot BC\\SA \bot BC\left( {SA \bot \left( {ABC} \right)} \right)\\AH \cap SA = \left\{ A \right\}\end{array} \right\} \Rightarrow BC \bot \left( {SAH} \right);BC \subset \left( {SBC} \right) \Rightarrow \left( {SAH} \right) \bot \left( {SBC} \right)\)
b) Ta có \(AH \bot BC,BC \bot SH\left( {BC \bot \left( {SAH} \right)} \right)\)
\( \Rightarrow \left[ {S,BC,A} \right] = \left( {SH,AH} \right) = \widehat {SHA}\)
Xét tam giác ABC vuông tại A có
\(\widehat {ABC} = {30^0} \Rightarrow \widehat {ACH} = {60^0}\)
Xét tam giác ACH vuông tại H có
\(\sin \widehat {ACH} = \frac{{AH}}{{AC}} \Rightarrow AH = a.\sin {60^0} = \frac{{a\sqrt 3 }}{2}\)
Xét tam giác SHA vuông tại A có
\(\tan \widehat {SHA} = \frac{{SA}}{{AH}} = \frac{{a\sqrt 3 }}{2}:\frac{{a\sqrt 3 }}{2} = 1 \Rightarrow \widehat {SHA} = {45^0}\)
Vậy \(\left[ {S,BC,A} \right] = {45^0}\)
Cho hình chóp \(S.ABC\) có \(SA = SB = SC = a,\widehat {ASB} = 90^\circ ,\widehat {BSC} = {60^ \circ }\) và \(\widehat {ASC} = {120^ \circ }\). Gọi \(I\) là trung điểm cạnh \(AC\). Chứng minh \(SI \bot \left( {ABC} \right)\).
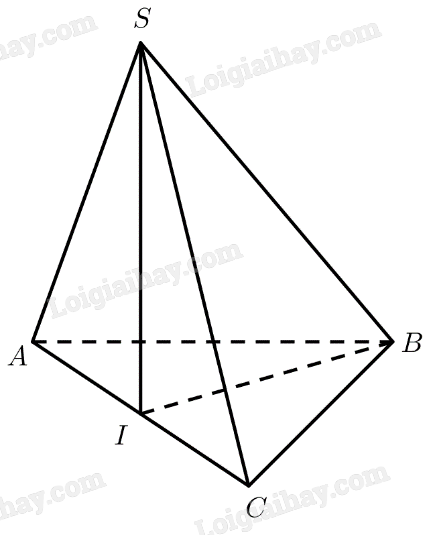
Xét tam giác \(SAC\) có:
\(AC = \sqrt {S{A^2} + S{C^2} - 2.SA.SC.\cos \widehat {ASC}} = a\sqrt 3 \)
\(SI\) là trung tuyến \( \Rightarrow SI = \frac{{\sqrt {2\left( {S{A^2} + S{C^2}} \right) - A{C^2}} }}{2} = \frac{a}{2}\)
Ta có: \(S{I^2} + A{I^2} = {\left( {\frac{a}{2}} \right)^2} + {\left( {\frac{{a\sqrt 3 }}{2}} \right)^2} = {a^2} = S{A^2}\)
\( \Rightarrow \Delta SAI\) vuông tại \(I \Rightarrow SI \bot AC\)
Xét tam giác \(SAB\) vuông tại \(S\) có: \(AB = \sqrt {S{A^2} + S{B^2}} = a\sqrt 2 \)
Xét tam giác \(SBC\) cân tại \(S\) có \(\widehat {BSC} = {60^ \circ }\) nên tam giác \(SBC\) đều. Vậy \(BC = a\)
Xét tam giác \(ABC\) có: \(A{B^2} + B{C^2} = {\left( {a\sqrt 2 } \right)^2} + {a^2} = 3{a^2} = A{C^2}\)
\( \Rightarrow \Delta ABC\) vuông tại \(B \Rightarrow BI = \frac{1}{2}AC = \frac{{a\sqrt 3 }}{2}\)
Xét tam giác \(SBI\) có: \(S{I^2} + B{I^2} = {\left( {\frac{a}{2}} \right)^2} + {\left( {\frac{{a\sqrt 3 }}{2}} \right)^2} = {a^2} = S{B^2}\)
\( \Rightarrow \Delta SBI\) vuông tại \(I \Rightarrow SI \bot BI\)
Ta có:
\(\left. \begin{array}{l}SI \bot AC\\SI \bot BI\end{array} \right\} \Rightarrow SI \bot \left( {ABC} \right)\)
Mọi ngừi vẽ hình và làm hết giùm mk câu này
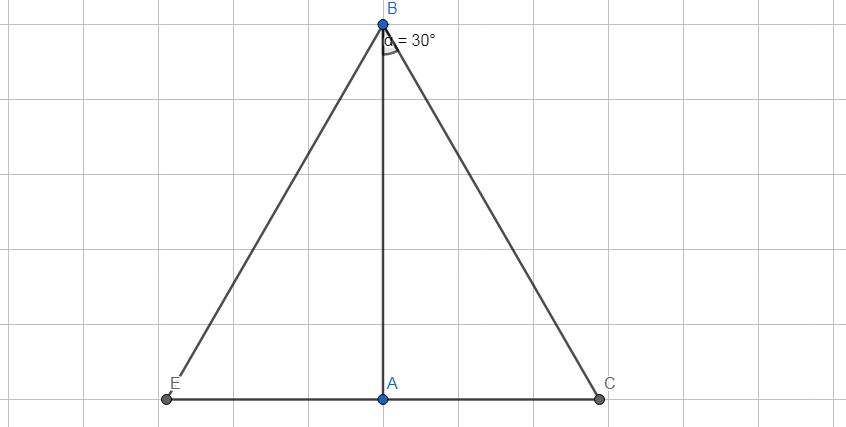
Cho \(\Delta\)\(ABC\) vuông tại A. \(\widehat{B}\) \(=30^0\). Trên tia đối của tia AC lấy điểm E sao cho AE = AC. Chứng minh
a) Tam giác BCE đều
b) \(AC=\dfrac{1}{2}BC\)
a) Xét tam giác ABC vuông tại A có:
\(\widehat{ABC}+\widehat{ACB}=90^0\)(phụ nhau)
=>300+\(\widehat{ACB}\)=900
=>\(\widehat{ACB}\)=600
Xét tam giác BEC có:
BA là đường cao (BA vuông góc với EC tại A)
BA là trung tuyến (A là trung điểm EC)
=>Tam giác BEC cân tại B mà \(\stackrel\frown{BCE}=60^0\)(cmt)
=>Tam giác BEC đều.
b) Ta có: AC=\(\dfrac{1}{2}\)CE mà CE=BC ( tam giác BCE đều)
=>AC=\(\dfrac{1}{2}\)BC