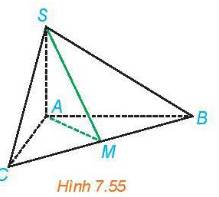
a) Xét tam giác ABC có AB = AC => tam giác ABC cân tại A mà M là trung điểm BC
=> \(AM \bot BC\) (1)
\(\begin{array}{l}SA \bot BC\left( {SA \bot \left( {ABCD} \right)} \right)\\ \Rightarrow BC \bot \left( {SAM} \right);SM \subset \left( {SAM} \right) \Rightarrow BC \bot SM\,\,\,\left( 2 \right)\end{array}\)
Từ (1), (2) ta có \(\widehat {SMA}\) là một góc phẳng của góc nhị diện [S, BC, A].
b) Xét tam giác ABC cân tại A có
\(\widehat {BAC} = {120^0} \Rightarrow \widehat {ACB} = {30^0}\)
\(\sin \widehat {ACB} = \frac{{AM}}{{AC}} \Leftrightarrow \tan {30^0} = \frac{{AM}}{a} \Leftrightarrow AM = \frac{a}{{\sqrt 3 }}\)
\(\tan \widehat {SMA} = \frac{{SA}}{{AM}} = \frac{a}{{2\sqrt 3 }}:\frac{a}{{\sqrt 3 }} = \frac{1}{2} \Rightarrow \widehat {SMA} = \arctan \frac{1}{2}\)