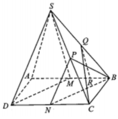
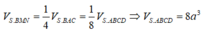Cho hình chóp S. ABCD có đáy là hình bình hành. Gọi M, N lần lượt là trung điểm cảu AB, SC; E là trung điểm SA. Thiết diện hình chóp khi cắt bởi mặt phẳng ( EMN ).
MV
Những câu hỏi liên quan
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm của AB, SC. Gọi I, K lần lượt là giao điểm của các đường thẳng AN, MN với mặt phẳng (SBD). Tỉ số
B
I
B
K
bằng
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm của AB, SC. Gọi I, K lần lượt là giao điểm của các đường thẳng AN, MN với mặt phẳng (SBD). Tỉ số B I B K bằng
![]()
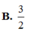
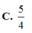
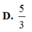
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm của AB, SC. Gọi I, K lần lượt là giao điểm của các đường thẳng AN, MN với mặt phẳng (SBD). Tỉ số BI/BK bằng A. 4/3 B. 3/2 C. 5/4 D. 5/3
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm của AB, SC. Gọi I, K lần lượt là giao điểm của các đường thẳng AN, MN với mặt phẳng (SBD). Tỉ số BI/BK bằng
A. 4/3
B. 3/2
C. 5/4
D. 5/3
Chọn A
Do B, I, K thẳng hàng, trong DABN kẻ MF//BI, FÎAN
=>F là trung điểm của AI. Suy ra BI/BK =4/3
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm của SA, SC. Biết thể tích của khối chóp S.BMN là
a
3
. Tính thể tích khối chóp S.ABCD A.
a
3
B. 4
a
3
C. 8
a
3
D. 16
a
3
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm của SA, SC. Biết thể tích của khối chóp S.BMN là a 3 . Tính thể tích khối chóp S.ABCD
A. a 3
B. 4 a 3
C. 8 a 3
D. 16 a 3
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh bên SA, SB, SC, SD (H.4.27). Chứng minh rằng tứ giác MNPQ là hình bình hành,
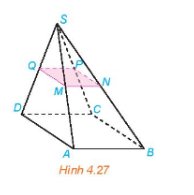
Xét tam giác SAB ta có: MN là đường trung bình suy ra MN // AB.
Tương tự ta có: NP // BC, PQ // CD, MQ // AD.
Mà ABCD là hình bình hành nên AB // CD, AD// CD, suy ra MN // PQ, MQ // NP.
Như vậy, MNPQ là hình bình hành.
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi O là giao điểm của AC và BD. Gọi M, N lần lượt là trung điểm của SB, SC. Tính tỉ số thể tích giữa hai khối chóp O.BCNM và S.ABCD.
Tự vẽ hình nhé!
Ta có:
\(V_{OBCNM}=\dfrac{1}{3}d\left(O;\left(BCNM\right)\right).S_{BCNM}=\dfrac{1}{3}.\dfrac{1}{2}d\left(A;\left(SBC\right)\right).\dfrac{3}{4}S_{SBC}=\dfrac{1}{8}V_{SABC}=\dfrac{1}{16}V_{SABCD}\)
\(\Rightarrow\dfrac{V_{OBCNM}}{V_{SABCD}}=\dfrac{1}{16}\)
Đúng 0
Bình luận (0)
Cho hình chóp S. ABCD, đáy là hình bình hành ABCD, các điểm M, N lần lượt thuộc các cạnh AB, SC. Phát biều nào sau đây là đúng? A. Thiết diện của (MND) với hình chóp là tam giác MND B. Thiết diện của (MND) với hình chóp là tứ giác NDMK, với K là giao điểm của SB với NI, I là giao điểm của MD với BC C. Thiết diện của (MND) với hình chóp là tứ giác NDMB D. Thiết diện của (MND) với hình chóp là tam giác NDB.
Đọc tiếp
Cho hình chóp S. ABCD, đáy là hình bình hành ABCD, các điểm M, N lần lượt thuộc các cạnh AB, SC. Phát biều nào sau đây là đúng?
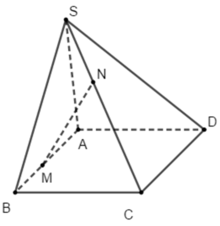
A. Thiết diện của (MND) với hình chóp là tam giác MND
B. Thiết diện của (MND) với hình chóp là tứ giác NDMK, với K là giao điểm của SB với NI, I là giao điểm của MD với BC
C. Thiết diện của (MND) với hình chóp là tứ giác NDMB
D. Thiết diện của (MND) với hình chóp là tam giác NDB.
Đáp án B
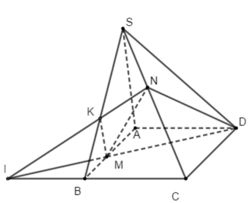
Trong mặt phẳng (ABCD) gọi I là giao điểm của MD và BC
Trong mặt phẳng (SBC) gọi K là giao điểm của IN và SB
Khi đó ta có: (MND) ∩ (SAB) = KM
(MND) ∩ (ABCD) = MD
(MND) ∩ (SBC) = KN
(MND) ∩ (SCD) = ND
Vậy thiết diện của mặt phẳng (MND) với hình chóp là tứ giác NDMK.
Đáp án B
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M,N,P,Q,R lần lượt là trung điểm của AB,CD,SC,SB,BM. Mặt phẳng (SDM) không song song với đường thẳng nào dưới đây? A.Đường thẳng CQ. B.Đường thẳng BP. C. Đường thẳng NP. D. Đường thẳng QR.
Đọc tiếp
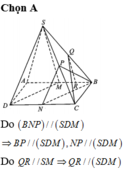
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M,N,P,Q,R lần lượt là trung điểm của AB,CD,SC,SB,BM. Mặt phẳng (SDM) không song song với đường thẳng nào dưới đây?
A.Đường thẳng CQ.
B.Đường thẳng BP.
C. Đường thẳng NP.
D. Đường thẳng QR.
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M,N,P,Q,R lần lượt là trung điểm của AB,CD,SC,SB,BM. Mặt phẳng (SDM) không song song với đường thẳng nào dưới đây? A. Đường thẳng CQ B. Đường thẳng BP C. Đường thẳng NP D. Đường thẳng QR
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M,N,P,Q,R lần lượt là trung điểm của AB,CD,SC,SB,BM. Mặt phẳng (SDM) không song song với đường thẳng nào dưới đây?
A. Đường thẳng CQ
B. Đường thẳng BP
C. Đường thẳng NP
D. Đường thẳng QR
Câu 3: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành b, Gọi M, N lần lượt là trung điểm của AB và SC. Tìm giao điểm của dường thẳng MN và (SBD) a, Tìm giao tuyến của (SAC) và (SBD)
Gọi giao của AC và BD là O
\(\left\{{}\begin{matrix}O\in AC\subset\left(SAC\right)\\O\in BD\subset\left(SBD\right)\end{matrix}\right.\Leftrightarrow O\in\left(SAC\right)\cap\left(SBD\right)\)
\(\left\{{}\begin{matrix}S\in\left(SAC\right)\\S\in\left(SBD\right)\end{matrix}\right.\Leftrightarrow S\in\left(SAC\right)\cap\left(SBD\right)\)
=>(SAC) giao (SBD)=SO
Đúng 0
Bình luận (0)