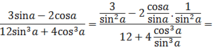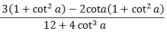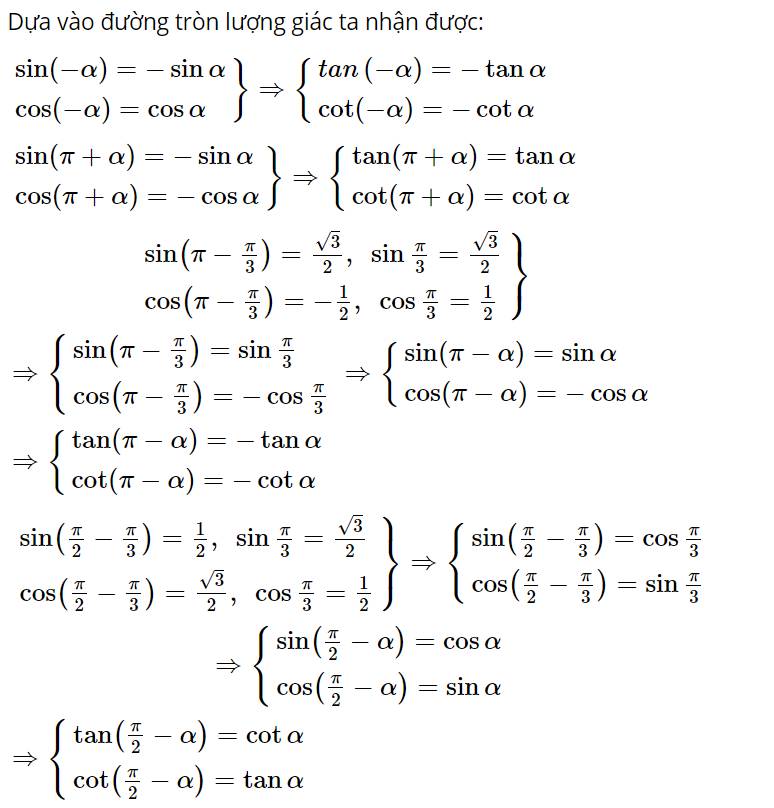Cho cota=-2.tìm các giá trị lượng giác
AQ
Những câu hỏi liên quan
Cho cota 3. Khi đó
3
sin
a
-
2
c
o
s
a
12
sin
3
a
+
4
cos
3...
Đọc tiếp
Cho cota = 3. Khi đó 3 sin a - 2 c o s a 12 sin 3 a + 4 cos 3 a có giá trị bằng
A. - 1 4
B. - 5 4
C. 3 4
D. 1 4
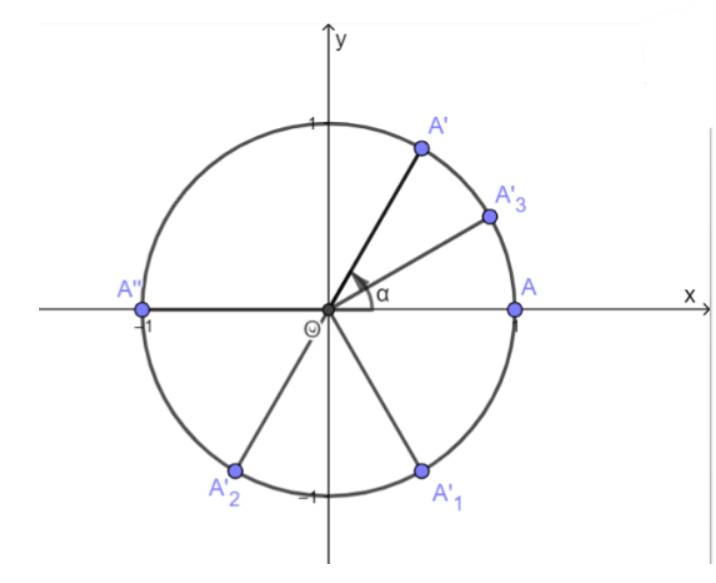
Cho \(\alpha = \frac{\pi }{3}\). Biểu diễn các góc lượng giác \( - \alpha ,\alpha + \pi ,\pi - \alpha ,\frac{\pi }{2} - \alpha \) trên đường tròn lượng giác và rút ra mỗi liên hệ giữ giá trị lượng giác của các góc này với giá trị lượng giác của góc \(\alpha \)
Tìm các giá trị lượng giác của góc lượng giác \(\alpha = 45^\circ \)
\(\sin \left( {45^\circ } \right) = \frac{{\sqrt 2 }}{2};\,\,\cos \left( {45^\circ } \right) = \frac{{\sqrt 2 }}{2};\,\,\tan \left( {45^\circ } \right) = \frac{1}{2};\,\,\cot \left( {45^\circ } \right) = 2\)
Đúng 0
Bình luận (0)
Cho tana + cota = m. Khi đó cot3a + tan3a có giá trị bằng
A. m3 + 3m
B. m3 - 3m
C. 3m3 + m
D. 3m3 + 3m
Chọn B.
Ta có cot3a + tan3a = ( tan a + cota) 3- 3tan a.cot a ( cot a + tan a)
= m3 - 3.1.m = m3 - 3m
Đúng 0
Bình luận (0)
Cho sinx=-0,8, với x ∈ (\(\pi\);\(\dfrac{3\pi}{2}\))
a)Tìm các giá trị lượng giác còn lại của góc x.
b)Tính giá trị của biểu thức P=2cos2x và Q = tan\(\left(2x+\dfrac{\pi}{3}\right)\)
a.Ta có : \(x\in\left(\pi;\dfrac{3}{2}\pi\right)\Rightarrow cosx< 0\)
\(cosx=-\sqrt{1-sin^2x}=-\sqrt{1-0,8^2}=-0,6\)
\(tanx=\dfrac{4}{3};cotx=\dfrac{3}{4}\)
b. cos 2x = \(cos^2x-sin^2x=0,6^2-0,8^2=-0,28\)
\(P=2.cos2x=-0,56\)
\(Q=tan\left(2x+\dfrac{\pi}{3}\right)=\dfrac{tan2x+tan\dfrac{\pi}{3}}{1-tan2x.tan\dfrac{\pi}{3}}=\dfrac{tan2x+\sqrt{3}}{1-tan2x.\sqrt{3}}\)
tan 2x = \(\dfrac{2tanx}{1-tan^2x}=\dfrac{\dfrac{2.4}{3}}{1-\left(\dfrac{4}{3}\right)^2}=\dfrac{-24}{7}\)
\(Q=\dfrac{-\dfrac{24}{7}+\sqrt{3}}{1+\dfrac{24}{7}.\sqrt{3}}\) \(=\dfrac{-24+7\sqrt{3}}{7+24\sqrt{3}}\)
Đúng 2
Bình luận (0)
Cho a, b là các số thực thuộc khoảng
0
;
π
2
thỏa mãn điều kiện cota - tan
π
2
-
b
a-b. Tính giá trị biểu thức
P
3
a
+
7
b
a...
Đọc tiếp
Cho a, b là các số thực thuộc khoảng 0 ; π 2 thỏa mãn điều kiện cota - tan π 2 - b = a-b. Tính giá trị biểu thức P = 3 a + 7 b a + b
A. P = 5
B. P = 2
C. P = 4
D. P = 6
Tìm các giá trị lượng giác của các góc 120o, 150o.
Các giá trị lượng giác của góc 120o là:
sin 120º = sin (180º – 60º) = sin 60º = √3/2.
cos 120º = cos(180º – 60º) = –cos 60º = –1/2
tan 120º = sin 120º / cos 120º = –√3
cot 120º = cos 120º / sin 120º = –1/√3
Các giá trị lượng giác của góc 150º là:
sin 150º = sin ( 180º – 30º ) = sin 30º = 1/2
cos 150º = –cos ( 180º – 30º ) = –cos 30º = (–√3)/2
tan 150º = sin 150º / cos 150º = –1/√3
cot 150º = cos 150º / sin 150º = –√3.
Đúng 0
Bình luận (0)
Nhắc lại khái niệm giá trị lượng giác của góc α, 0o ≤ α ≤ 180o.
Ta có thể mở rộng khái niệm giá trị lượng giác cho các cung và góc lượng giác.
Các số sinα; cosα; tanα; cotα được gọi là giá trị lượng giác của góc α, với 0o ≤ α ≤ 180o.
Đúng 0
Bình luận (0)
Bài 1: Cho tam giác MNP vuông tại N, biết rằng MP=10dm,MN=6cm.Tính tỉ số lượng giác của hai góc nhọn M và P Bài 2: Cho sinA=0,35.Tính tanA , cotA , cosA ?
Bài 2:
\(\cos\widehat{A}=\dfrac{3\sqrt{39}}{20}\)
\(\tan\widehat{A}=\dfrac{7}{20}:\dfrac{3\sqrt{39}}{20}=\dfrac{7}{3\sqrt{39}}=\dfrac{7\sqrt{39}}{117}\)
\(\cot\widehat{A}=\dfrac{3\sqrt{39}}{7}\)
Đúng 0
Bình luận (0)