Triển khai các biểu thức sau theo hằng đẳng thức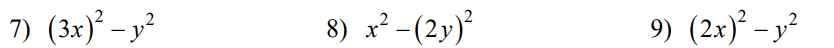
PT
Những câu hỏi liên quan
Triển khai các biểu thức sau theo hằng đẳng thức:
(x - 6) (6 + x)
\(\left(x-6\right)\left(6+x\right)=\left(x-6\right)\left(x+6\right)=x^2-6^2=x^2-36\)
Đúng 2
Bình luận (0)
Sử dụng hằng đẳng thức khai triển và thu gọn biểu thức sau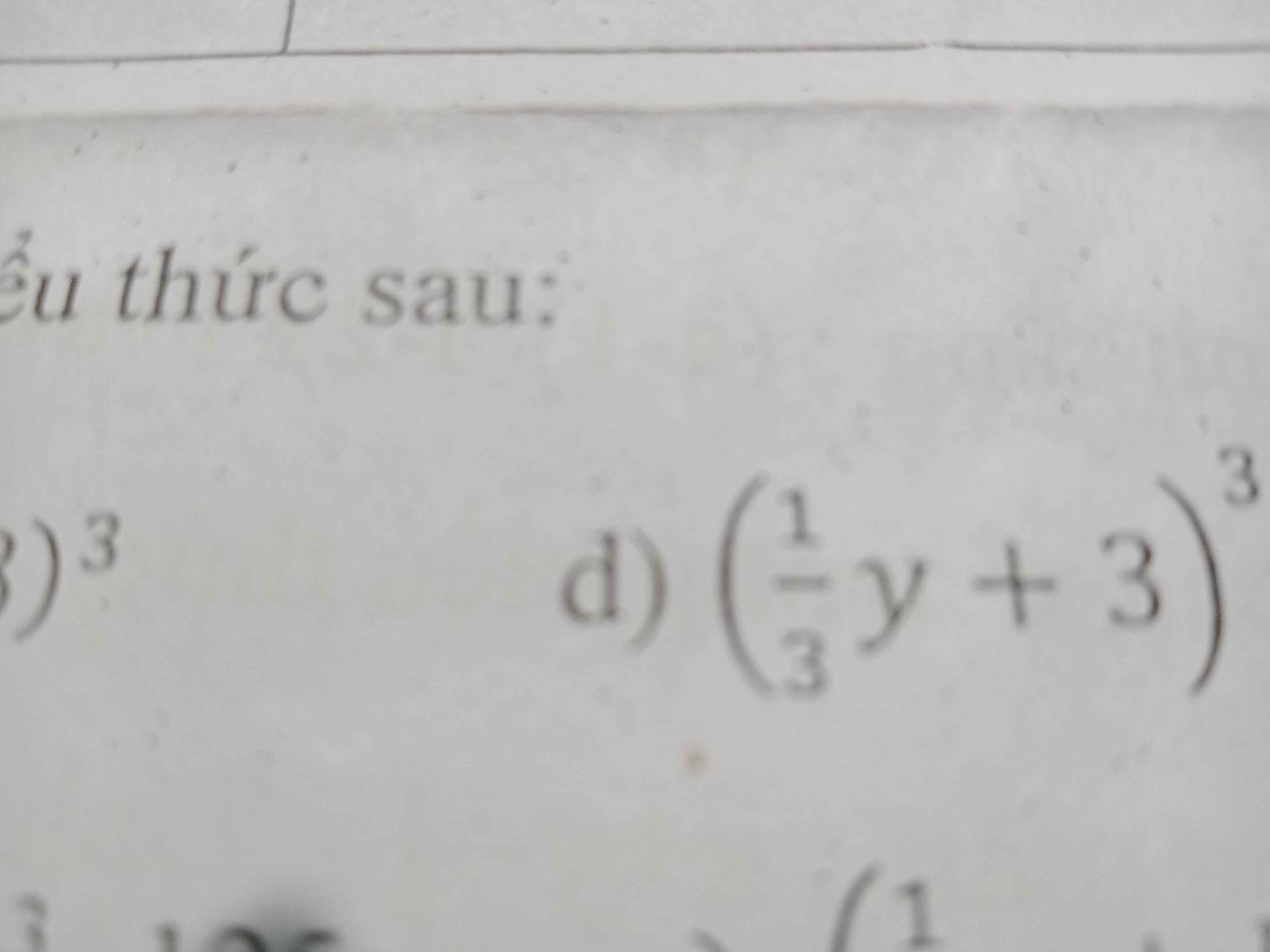
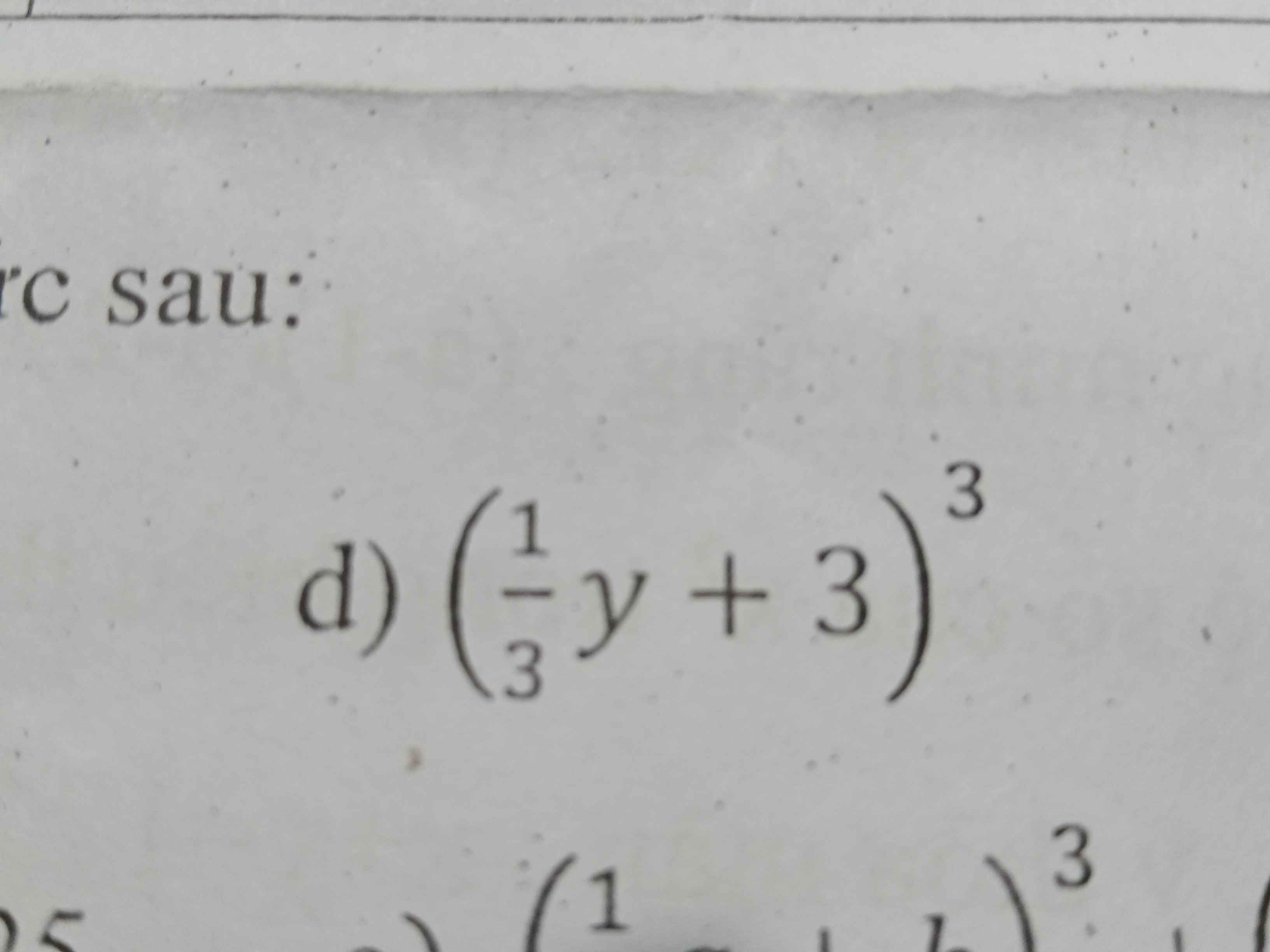
(1𝑦/3+3)^3
(𝑦/3+3)^3
(𝑦/3+3⋅3/3)^3
(𝑦+3⋅3/3)^3
(𝑦+9/3)^3
Đúng 0
Bình luận (0)
\(\left(\dfrac{1}{3}y+3\right)^3=\dfrac{1}{27}y^3+y^2+9y+27\)
Đúng 0
Bình luận (0)
Trong các khai triển hằng đẳng thức sau, khai triển nào sai? A.
(
A
+
B
)
2
A
2
+
2
A
B
+
B...
Đọc tiếp
Trong các khai triển hằng đẳng thức sau, khai triển nào sai?
A. ( A + B ) 2 = A 2 + 2 A B + B 2
B. ( A – B ) 3 = A 3 – 3 A 2 B – 3 A B 2 + B 3
C. A 2 – B 2 = ( A – B ) ( A + B )
D. A 3 – B 3 = ( A – B ) ( A 2 + A B + B 2 )
( A – B ) 3 = ( A + ( - B ) ) 3 = A 3 + 3 . A 2 . ( - B ) + 3 . A . ( - B ) 2 + ( - B ) 3 = A 3 – 3 A 2 B + 3 A B 2 – B 3 = > ( A – B ) 3 = A 3 – 3 A 2 B – 3 A B 2 + B 3
là sai
Đáp án cần chọn là: B
Đúng 0
Bình luận (0)
Sử dụng hằng đẳng thức khai triển và thu gọn biểu thức sau (1phần 3y+3)^3
\(\left(\dfrac{1}{3y+3}\right)^3=\dfrac{1}{\left(3y+3\right)^3}=\dfrac{1}{27y^3+81y^2+81y+27}\)
Đúng 0
Bình luận (0)
\(\left(\dfrac{1}{3y+3}\right)^3=\dfrac{1^3}{\left(3y+3\right)^3}=\dfrac{1}{27\left(y^3+3y^2+3y+1\right)}\)
Đúng 0
Bình luận (0)
\(\left(\dfrac{1}{3}y+3\right)^3=\dfrac{1}{27}y^3+y^2+9y+27\)
Đúng 0
Bình luận (0)
Dùng hằng đẳng thức để khai triển và thu gọn các biểu thức sau:
(a^3+ab+b^2)(a^2-ab+b^2)-(a^4+b^4)
Ta có:(a2+ab+b2)(a2-ab+b2)-(a4+b4)
= (a2+b2)2-a2b2-a4-b4=a4+2a2b2+b4-a2b2-a4-b4=a2b2
Đúng 2
Bình luận (0)
Ta có:(a2+ab+b2)(a2-ab+b2)-(a4+b4)
= (a2+b2)2-a2b2-a4-b4=a4+2a2b2+b4-a2b2-a4-b4=a2b2
Đúng 1
Bình luận (0)
Khai triển các hằng đẳng thức sau : (x + 3)³ .
Sử dụng hằng đẳng thức khai triển và thu gọn biểu thức sau. A/. (x+y)^3-(x-y)^3
a: Ta có: \(\left(x+y\right)^3-\left(x-y\right)^3\)
\(=x^3+3x^2y+3xy^2+y^3-x^3+3x^2y-3xy^2+y^3\)
\(=6x^2y+2y^3\)
Đúng 1
Bình luận (0)
\(\left(x+y\right)^3-\left(x-y\right)^3\)
\(=\left(x+y-x+y\right)^3+3\left(x+y\right)\left(x-y\right)\left(x+y-x+y\right)\)
\(=8y^3+6y\left(x^2-y^2\right)\)
\(=8y^3+6x^2y-6y^3\)
\(=2y^3+6x^2y\)
Đúng 1
Bình luận (0)
dùng hằng đẳng thức để khai triển và thu gọn biểu thức sau a, (6x2 +1/3)2 b,(5x-4y)2
Khai triển các hằng đẳng thức sau : A. (x - 6)² ; B. (x + 3)³ .
a: \(=x^2-12x+36\)
b: \(=x^3+9x^2+27x+27\)
Đúng 1
Bình luận (0)








