mng làm nhanh giúp mik nha.Làm bao nhiêu bào cx đc ah(lm hết càng tốt nhé).Cảm ơn mng gất nhìu
DM
Những câu hỏi liên quan

giúp mik vs nhé, cảm mơn rất nhìu ( làm 1, 2 bài th cx đc, lm hết càng tốt nhé)
ta có Cu ko tác dụng được vs H2SO4
-> 2,24 lít khí H2 đc tạo ra là do phản ứng HH của Fe va H2SO4
\(PTHH:\) \(Fe+H_2SO_4->FeSO_4+H2\)
n H2 = 2,24 :22,4=0,1 mol
n H2 = n Fe =0,1 mol
m Fe = 0,1.56=5,6 g
m Cu = 10-5,6=4,4 g
vậy giá trị của x là 4,4 g
Đúng 0
Bình luận (0)
26
PTHH : \(Zn+2HCl->ZnCl_2+H_2\)
n Zn = 6,5:65=0,1 mol
n ZnCl2 = n Zn =0,1 mol
m ZnCl2 = 0,1.(65+35,5.2)=13,6 g
Đúng 0
Bình luận (1)
ta có Cu ko tác dụng được vs H2SO4
-> 2,24 lít khí H2 đc tạo ra là do phản ứng HH của Fe va H2SO4
PTHH:PTHH: Fe+H2SO4−>FeSO4+H2Fe+H2SO4−>FeSO4+H2
n H2 = 2,24 :22,4=0,1 mol
n H2 = n Fe =0,1 mol
m Fe = 0,1.56=5,6 g
m Cu = 10-5,6=4,4 g
vậy giá trị của x là 4,4 g
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
mng làm nhanh giúp mik nha lm bao nhiêu bài cx đc ah.Cảm mơm mng nha
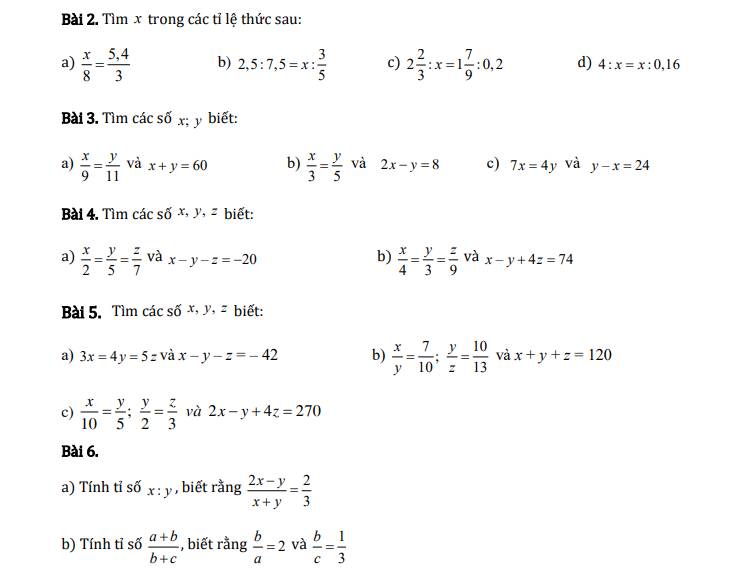
Bài 2
a) x/8 = 5,4/3
x = 8 . 5,4/3
x = 14,4
b) 2,5 : 7,5 = x : 3/5
x = 3/5 × 1/3
x = 1/5
c) 2 2/3 : x = 1 7/9 : 0,2
8/3 : x = 16/9 : 1/5
x = 8/3 : (16/9 : 1/5)
x = 8/3 : 80/9
x = 3/10
d) 4/x = x/0,16
x² = 4 . 0,16
x² = 0,64
x = 0,8 hoặc x = -0,8
Đúng 2
Bình luận (0)
Bài 3
a) x/9 = y/11 và x + y = 60
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
x/9 + y/11 = (x + y)/(9 + 11) = 60/20 = 3
x/9 = 3 ⇒ x = 9.3 = 27
y/11 = 3 ⇒ y = 11.3 = 33
Vậy x = 27; y = 33
b) x/3 = y/5 ⇒ 2x/6 = y/5 và 2x - y = 8
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
2x/6 = y/5 = (2x - y)/(6 - 5) = 8/1 = 8
2x/6 = 8 ⇒ x = 6.8:2 = 24
y/5 = 8 ⇒ y = 5.8 = 40
Vậy x = 24; y = 40
c) 7x = 4y ⇒ y/7 = x/4 và y - x = 24
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
y/7 = x/4 = (y - x)/(7 - 4) = 24/3 = 8
x/4 = 8 ⇒ x = 4.8 = 32
y/7 = 8 ⇒ y = 7.8 = 56
Vậy x = 32; y = 56
Đúng 2
Bình luận (0)
Bài 4
a) x/2 = y/5 = z/7 và x - y - z = -20
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
x/2 = y/5 = z/7 = (x - y - z)/(2 - 5 - 7) = -20/(-10) = 2
x/2 = 2 ⇒ x = 2.2 = 4
y/5 = 2 ⇒ y = 5.2 = 10
z/7 = 2 z = 7.2 = 14
Vậy x = 4; y = 10; z = 14
b) x/4 = y/3 = z/9 ⇒ x/4 = y/3 = 4z/36
Và x - y + 4z = 74
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
x/4 = y/3 = 4z/36 = (x - y + 4z)/(4 - 3 + 36) = 74/37 = 2
x/4 = 2 ⇒ x = 4.2 = 8
y/3 = 2 ⇒ y = 3.2 = 6
z/9 = 2 ⇒ z = 9.2 = 18
Vậy x = 8; y = 6; z = 18
Đúng 2
Bình luận (0)
Xem thêm câu trả lời
Trên thửa ruộng đó người ta trồng lúa và khi thu hoạch được tất cả 2 tấn thóc. Hỏi mỗi m vuông thu hoạch đc bao nhiêu kg thóc?
-GIÚP MIK VỚI, MIK ĐAG CẦN GẤP
- AI TRLOI ĐẦU TIÊN MIK TIK CHO NHÉ
- CẢM ƠN MNG NHÌU NHÌU(^_^)
làm câu nào cx đc, càng nhiều càng tốt, e cảm ơn nhìu
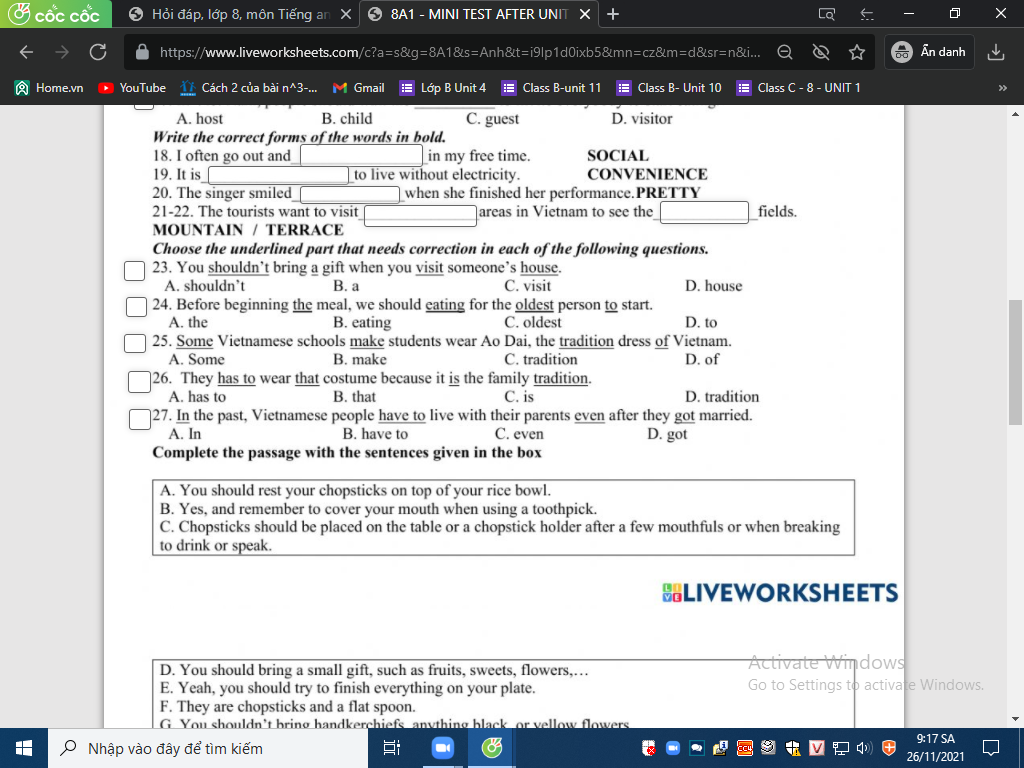
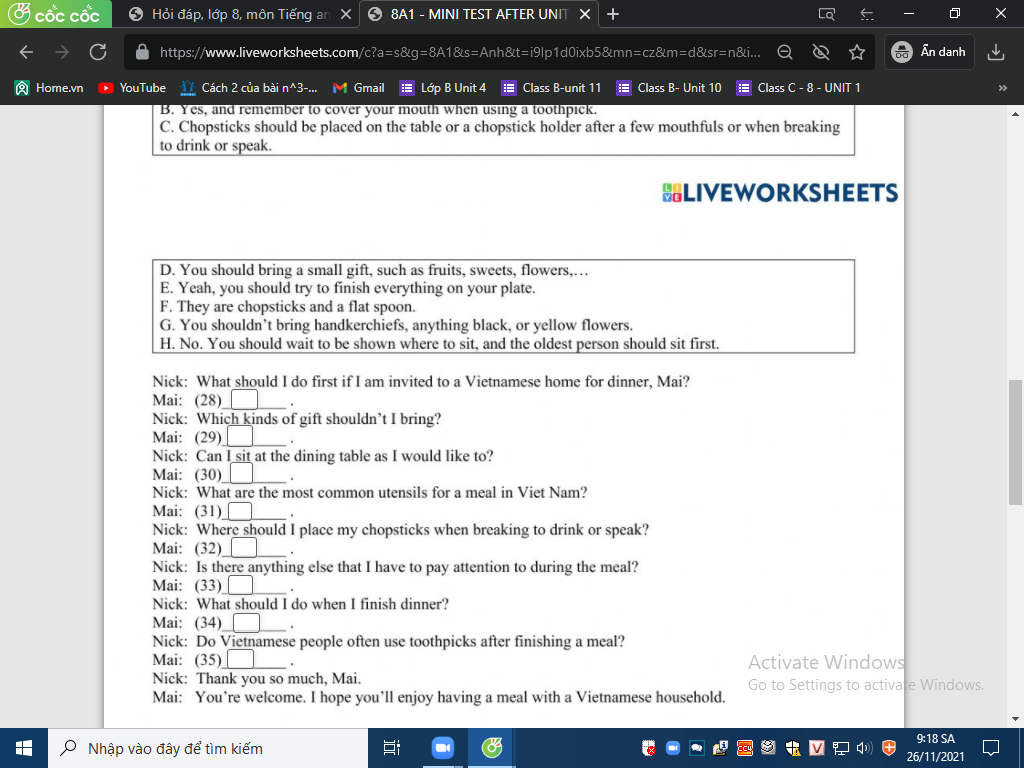
Mng giúp mik vs bn của mik lm sai, các bạn có thể sửa lại và chọn đáp án đúng nhất đc ko ạ? Lm ơn giúp mik, cảm ơn.
Đọc tiếp
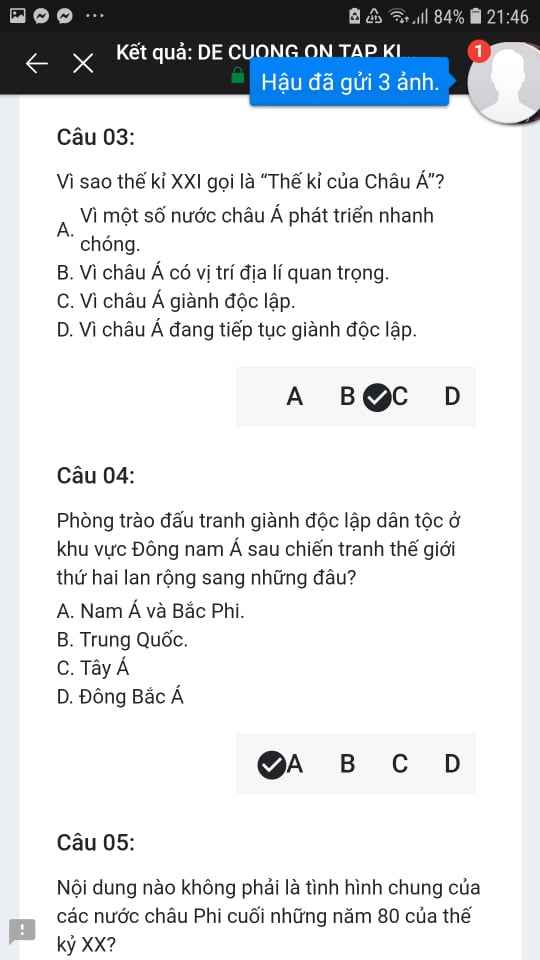
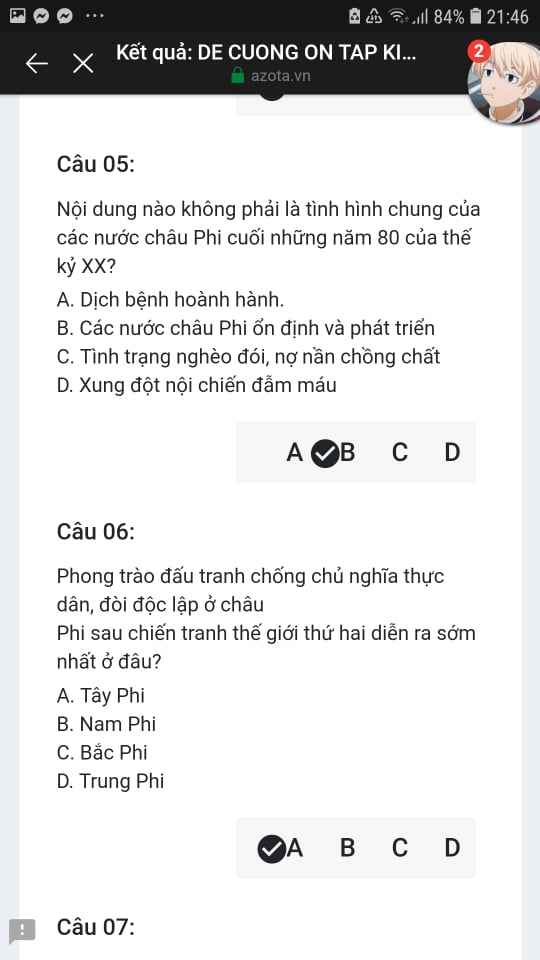
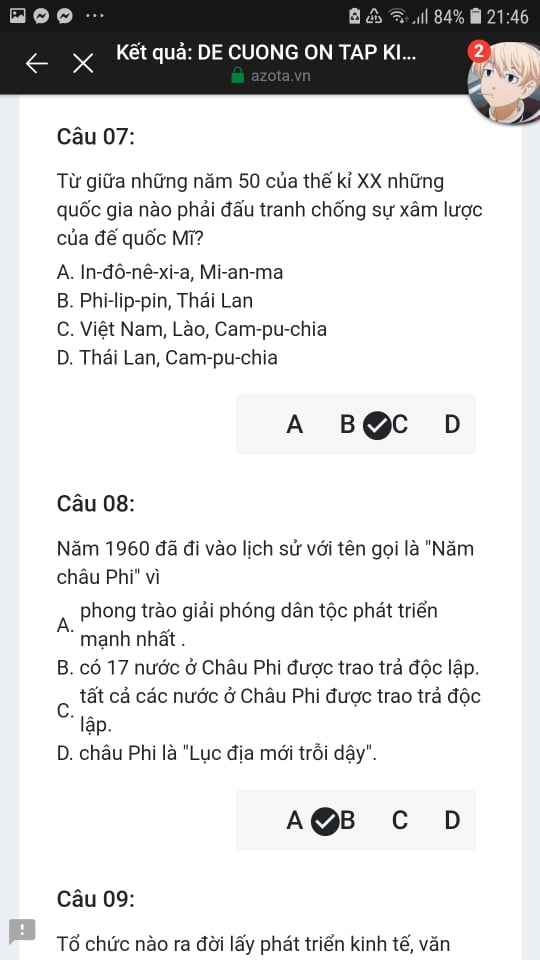

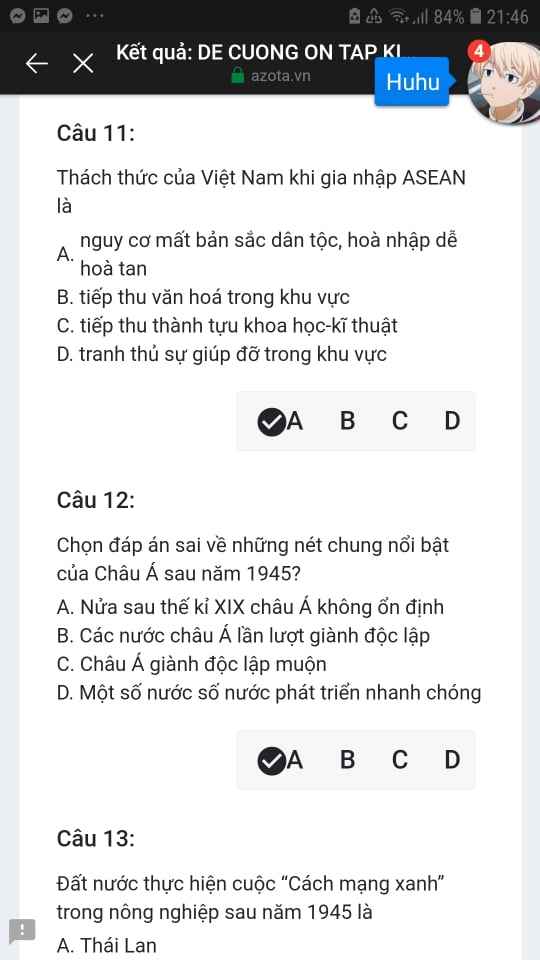
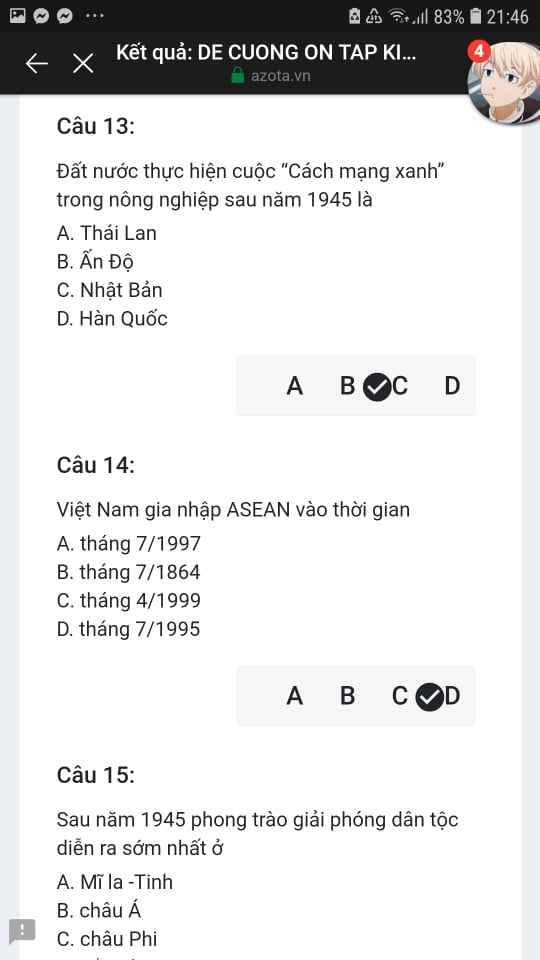
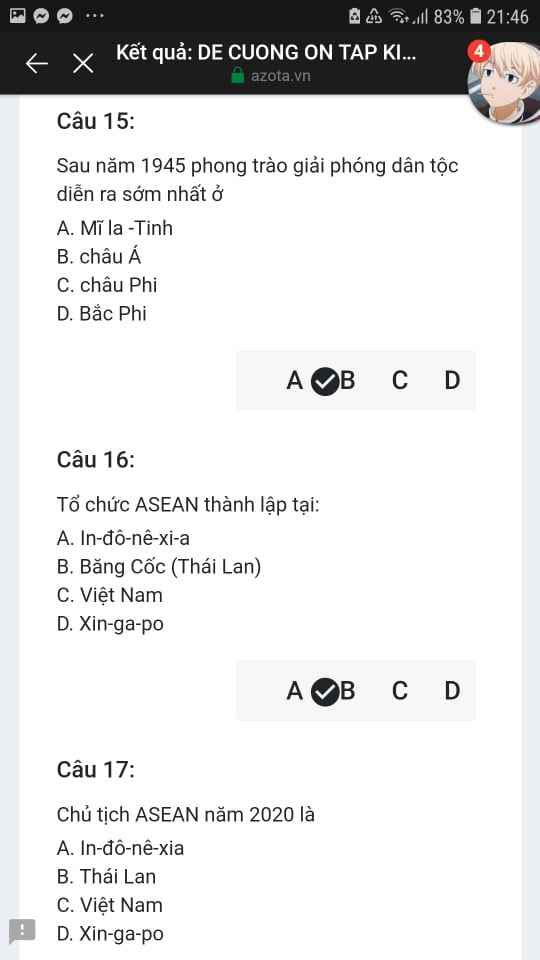


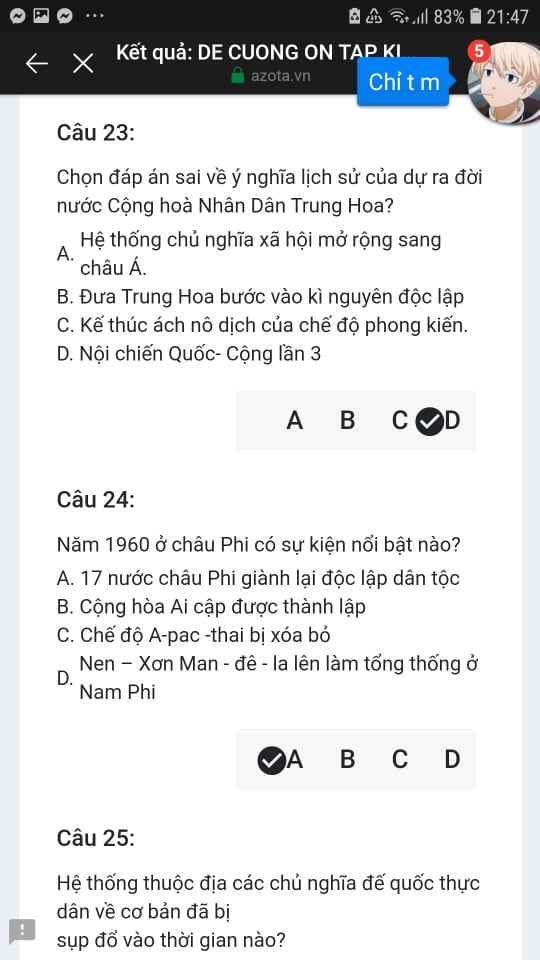
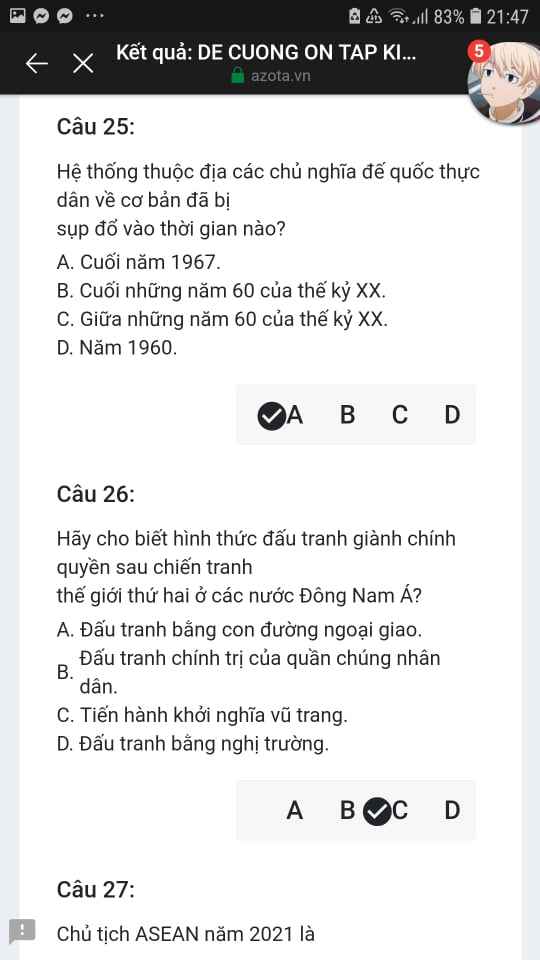
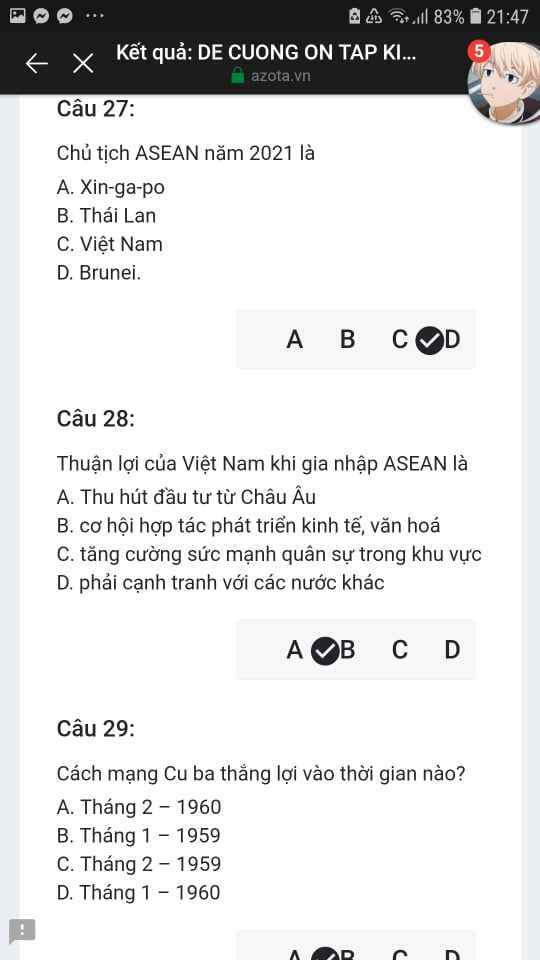
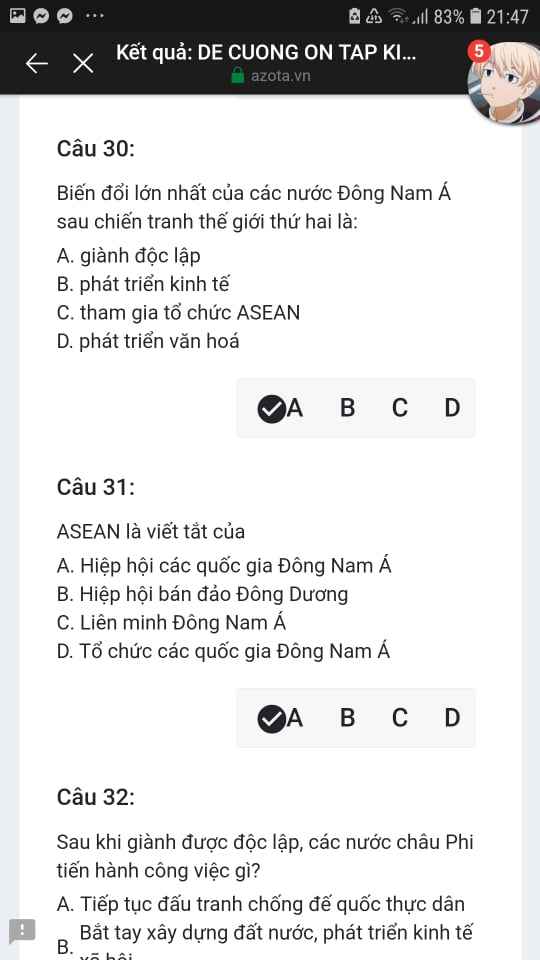
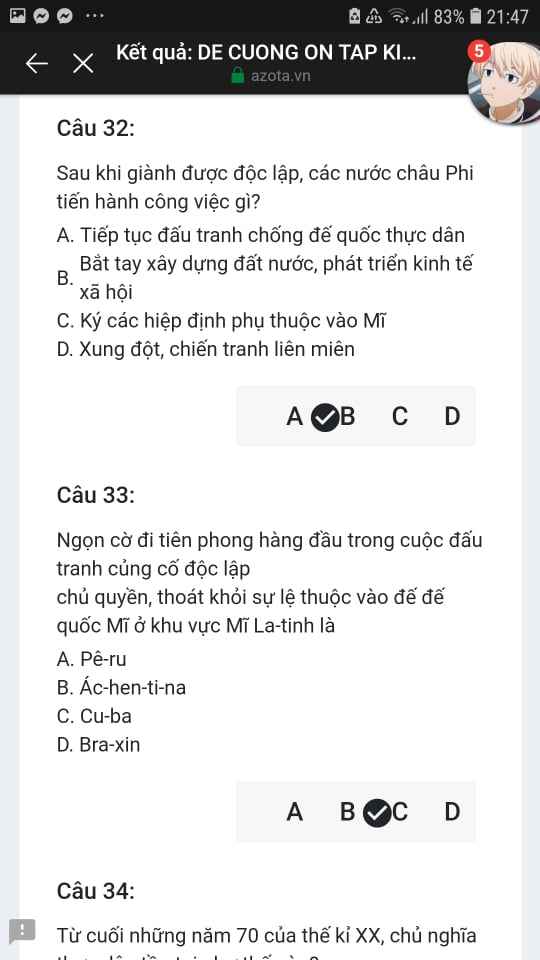

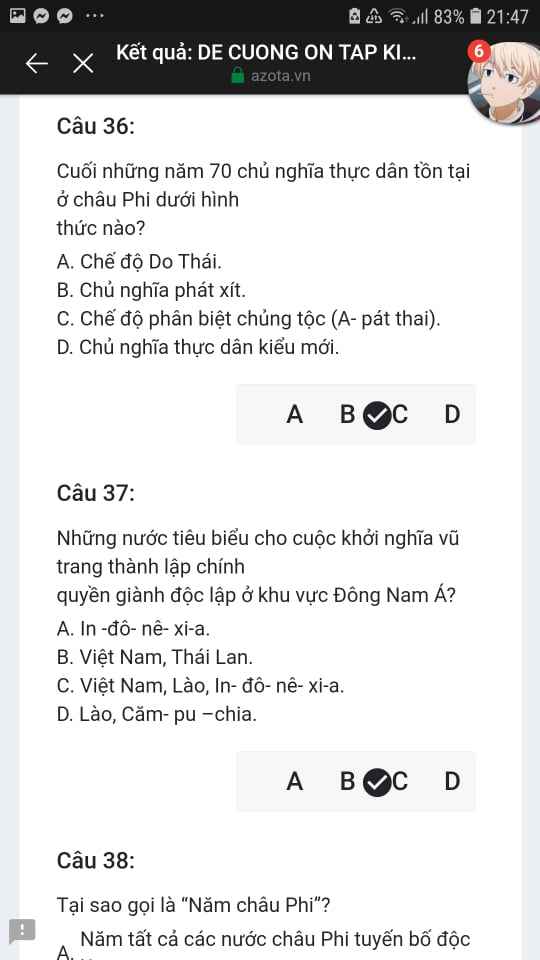
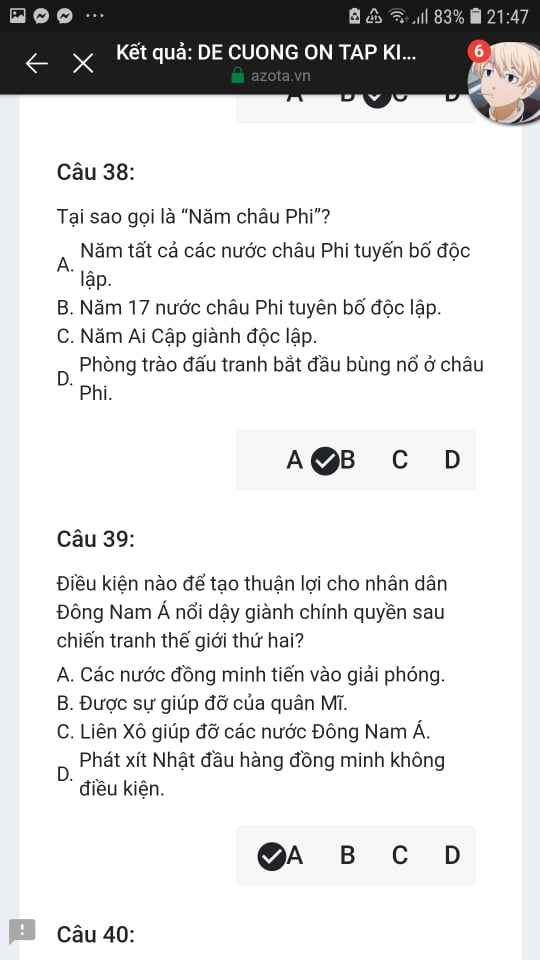

Mng giúp mik vs bn của mik lm sai, các bạn có thể sửa lại và chọn đáp án đúng nhất đc ko ạ? Lm ơn giúp mik, cảm ơn.![]()
Mọi người giúp em bài 4 5 6 với ạ cảm ơn mng gất nhiều
Bài 4:
a. ĐKXĐ: \(\left\{\begin{matrix} x-1\geq 0\\ x-1\neq 2\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x\geq 1\\ x\neq 3\end{matrix}\right.\)
b. \(B=\frac{x-3}{\frac{x-1-2}{\sqrt{x-1}+\sqrt{2}}}=\sqrt{x-1}+\sqrt{2}\)
\(x=4(2-\sqrt{3})\Rightarrow x-1=7-4\sqrt{3}=(2-\sqrt{3})^2\)
\(\Rightarrow \sqrt{x-1}=2-\sqrt{3}\Rightarrow B=\sqrt{x-1}+\sqrt{2}=2-\sqrt{3}+\sqrt{2}\)
c.
$\sqrt{x-1}\geq 0$ với mọi $x\geq 1; x\neq 3$
$\Rightarrow B=\sqrt{x-1}+\sqrt{2}\geq \sqrt{2}$
Vậy $B_{\min}=\sqrt{2}$ khi $x=1$
Đúng 0
Bình luận (0)
Bài 5:
\(C=\frac{x-2\sqrt{xy}+y+4\sqrt{xy}}{\sqrt{x}+\sqrt{y}}-\frac{\sqrt{xy}(\sqrt{x}-\sqrt{y})}{\sqrt{xy}}\)
\(=\frac{(\sqrt{x}+\sqrt{y})^2}{\sqrt{x}+\sqrt{y}}-(\sqrt{x}-\sqrt{y})=(\sqrt{x}+\sqrt{y})-(\sqrt{x}-\sqrt{y})\)
\(=2\sqrt{y}\) vẫn phụ thuộc vào biến $y$ bạn ạ. Bạn xem lại đề.
Đúng 0
Bình luận (0)
Bài 6:
a. ĐKXĐ: $x\geq 0; x\neq 4$
\(D=\left[\frac{\sqrt{x}}{(\sqrt{x}-2)(\sqrt{x}+2)}-\frac{2(\sqrt{x}+2)}{(\sqrt{x}-2)(\sqrt{x}+2)}+\frac{\sqrt{x}-2}{(\sqrt{x}+2)(\sqrt{x}-2)}\right]:\frac{(\sqrt{x}+2)(\sqrt{x}-2)+10-x}{\sqrt{x}+2}\)
\(=\frac{-6}{(\sqrt{x}-2)(\sqrt{x}+2)}:\frac{6}{\sqrt{x}+2}=\frac{-6}{(\sqrt{x}-2)(\sqrt{x}+2)}.\frac{\sqrt{x}+2}{6}=\frac{1}{2-\sqrt{x}}\)
b.
Để $D>0\Leftrightarrow \frac{1}{2-\sqrt{x}}>0$
$\Leftrightarrow 2-\sqrt{x}>0$
$\Leftrightarrow 2>\sqrt{x}$
$\Leftrightarrow 0\leq x< 4$
Kết hợp với đkxđ suy ra $0\leq x< 4$
Đúng 0
Bình luận (0)
Mng ơi! Mng bt chỗ nào bán sách để học TA tốt thì chỉ e vs. Hoặc chỉ e cách hc tốt TA cũng đc=(((. Do e bị mất gốc mà hong bt hc lại từ đâu hết:'((( Mong mng giúp đỡ. Em cảm ơn<3333
Um có nhiều web học tiếng anh lắm ạ . Ví dụ như Langking dom hoặc Tieka . Tieka chỉ cần đóng 1 -> 2 triệu là có thể học từ giờ đến lớp 12 luôn ấy ạ . Có đủ bài giảng với có bài thực hành
Đúng 0
Bình luận (0)
sách thì mình ko biết, nhưng cách học thì bạn cứ bắt đầu từ một cấu trúc nào đó, làm đi làm lại nhiều dạng nthe rồi chuyển tiếp sang những cấu trúc tiếp theo. Học thêm với một gv là cách tốt hơn tự học nhé
Đúng 2
Bình luận (0)
CẢM ƠN TRƯỚC ^^ (lm bnhiêu cũng đc == lm hết càng tốt ạ •cảm ơn• ^^ [Mong ai đó giúp🙏]
câu 63: A
câu 64: B
câu 65: C
mấy câu còn lại phải từ từ đã!
Đúng 1
Bình luận (0)
Câu 63: A
Câu 64: B
Câu 65: C
Câu 71: D
Câu 72: A
Câu 73: C
Câu 74: B
Câu 75: C
Câu 76: B
Câu 77: A
Câu 78: C
Câu 79: B
Câu 80: C
Đúng 1
Bình luận (1)
câu 71: D
câu 72: A
câu 73: C
câu 74: B
câu 75: C
tick đi! ko sai đâu
Đúng 1
Bình luận (0)
giúp mik với ạ, mik đang cần gấp! cảm ơn mng nhìu!
Đọc tiếp
giúp mik với ạ, mik đang cần gấp! cảm ơn mng nhìu!
\(a,\) Áp dụng t/c dtsbn:
\(\dfrac{x}{10}=\dfrac{y}{6}=\dfrac{z}{21}=\dfrac{5x}{50}=\dfrac{2z}{42}=\dfrac{5x+y-2z}{50+6-42}=\dfrac{28}{14}=2\\ \Rightarrow\left\{{}\begin{matrix}x=20\\y=12\\z=42\end{matrix}\right.\\ b,\dfrac{x}{3}=\dfrac{y}{4}\Rightarrow\dfrac{x}{15}=\dfrac{y}{20};\dfrac{y}{5}=\dfrac{z}{7}\Rightarrow\dfrac{y}{20}=\dfrac{z}{28}\\ \Rightarrow\dfrac{x}{15}=\dfrac{y}{20}=\dfrac{z}{28}\)
Áp dụng t/c dtsbn
\(\dfrac{x}{15}=\dfrac{y}{20}=\dfrac{z}{28}=\dfrac{2x}{30}=\dfrac{3y}{60}=\dfrac{2x+3y-z}{30+60-28}=\dfrac{124}{62}=2\\ \Rightarrow\left\{{}\begin{matrix}x=30\\y=40\\z=56\end{matrix}\right.\)
\(c,\) Áp dụng t/c dtsbn
\(\dfrac{2x}{3}=\dfrac{3y}{4}=\dfrac{4z}{5}=\dfrac{x}{\dfrac{3}{2}}=\dfrac{y}{\dfrac{4}{3}}=\dfrac{z}{\dfrac{5}{4}}=\dfrac{x+y+z}{\dfrac{3}{2}+\dfrac{4}{3}+\dfrac{5}{4}}=\dfrac{49}{\dfrac{49}{12}}=12\\ \Rightarrow\left\{{}\begin{matrix}x=12\cdot\dfrac{3}{2}=18\\y=12\cdot\dfrac{4}{3}=16\\z=12\cdot\dfrac{5}{4}=15\end{matrix}\right.\)
\(d,\) Đặt \(\dfrac{x}{2}=\dfrac{y}{3}=k\Rightarrow x=2k;y=3k\)
\(xy=54\Rightarrow2k\cdot3k=54\Rightarrow k^2=9\Rightarrow\left[{}\begin{matrix}k=3\\k=-3\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=6;y=9\\x=-6;y=-9\end{matrix}\right.\)
\(e,\) Đặt \(\dfrac{x}{5}=\dfrac{y}{3}=k\Rightarrow x=5k;y=3k\)
\(x^2-y^2=4\Rightarrow25k^2-9k^2=4\Rightarrow16k^2=4\Rightarrow k^2=\dfrac{1}{4}\\ \Rightarrow\left[{}\begin{matrix}k=\dfrac{1}{2}\\k=-\dfrac{1}{2}\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=\dfrac{5}{2};y=\dfrac{3}{2}\\x=-\dfrac{5}{2};y=-\dfrac{3}{2}\end{matrix}\right.\)
\(f,\) Áp dụng t/c dtsbn:
\(\dfrac{x}{y+z+1}=\dfrac{y}{z+x+1}=\dfrac{z}{x+y-2}=\dfrac{x+y+z}{2\left(x+y+z\right)}=\dfrac{1}{2}=x+y+z\)
\(\Rightarrow\left\{{}\begin{matrix}2x=y+z+1\\2y=x+z+1\\2z=x+y-2\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x+y+z=3x-1\\x+y+z=3y-1\\x+y+z=3z+2\end{matrix}\right.\\ \Rightarrow\left\{{}\begin{matrix}3x-1=\dfrac{1}{2}\\3y-1=\dfrac{1}{2}\\3z+2=\dfrac{1}{2}\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=\dfrac{1}{2}\\y=\dfrac{1}{2}\\z=-\dfrac{1}{2}\end{matrix}\right.\)
Đúng 2
Bình luận (0)






