Cho tam giác ABC vuông tại A có AB=15cm, AC=20cm. Độ dài cạnh BC=25cm và số đo góc B lần lượt là
NK
Những câu hỏi liên quan
cho tam giác ABC có AB 15cm , AC 20cm , BC 25cm a, chứng minh tam giác ABC vuông tại A . tính độ dài đướng cao AH b, đường phân giác của góc A cắt BC tại D . từ kẻ DE và DF lần lượt vuông góc với AB vầ ÁC ( E thuộc AB , F thuộc AC ) . tứ giác AEDF là hình gì . vì sao . tính diện tích tứ giác AEDF .c, chứng minh rằng : EF*EF + BC*BC EC*EC + BF*BF ( độ dài và diện tích làm tròn đến số thập phan thứ ba , góc làm tròn đến phút )
Đọc tiếp
cho tam giác ABC có AB = 15cm , AC = 20cm , BC = 25cm
a, chứng minh tam giác ABC vuông tại A . tính độ dài đướng cao AH
b, đường phân giác của góc A cắt BC tại D . từ kẻ DE và DF lần lượt vuông góc với AB vầ ÁC ( E thuộc AB , F thuộc AC ) . tứ giác AEDF là hình gì . vì sao . tính diện tích tứ giác AEDF .
c, chứng minh rằng : EF*EF + BC*BC = EC*EC + BF*BF
( độ dài và diện tích làm tròn đến số thập phan thứ ba , góc làm tròn đến phút )
Tam giác \(ABC\) có \(AB = 15cm,AC = 20cm,BC = 25cm\). Đường phân giác của góc \(BAC\)cắt \(BC\) tại \(D\). Qua \(D\) vẽ \(DE//AB\left( {E \in AC} \right)\).
a) Tính độ dài các đoạn thẳng \(BD,DC\) và \(DE\).
b) Chứng minh \(ABC\) là tam giác vuông. Tính diện tích tam giác \(ABC\).
c) Tính diện tích tam giác \(ADB,ADE\) và \(DCE\).
a) Ta có: \(BD + DC = BC \Rightarrow DC = BC - BD = 25 - BD\)
Vì \(AD\) là phân giác của góc \(BAC\) nên theo tính chất đường phân giác ta có:
\(\frac{{BD}}{{DC}} = \frac{{AB}}{{AC}} \Leftrightarrow \frac{{BD}}{{25 - BD}} = \frac{{15}}{{20}} \Leftrightarrow 20.BD = 15.\left( {25 - BD} \right) \Rightarrow 20.BD = 375 - 15.BD\)
\( \Leftrightarrow 20BD + 15BD = 375 \Leftrightarrow 35BD = 375 \Rightarrow BD = \frac{{375}}{{35}} = \frac{{75}}{7}\)
\( \Rightarrow DC = 25 - \frac{{75}}{7} = \frac{{100}}{7}\)
Vậy \(BD = \frac{{75}}{7}cm;DC = \frac{{100}}{7}cm\).
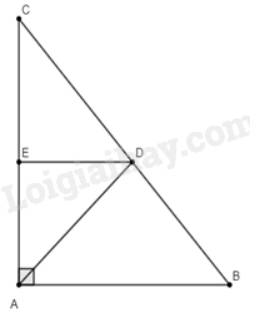
Vì \(DE//AB\) nên \(\frac{{DC}}{{BC}} = \frac{{DE}}{{AB}} \Rightarrow \frac{{\frac{{100}}{7}}}{{25}} = \frac{{DE}}{{15}} \Leftrightarrow DE = \frac{{100}}{7}.15:25 = \frac{{60}}{7}\) (hệ quả của định lí Thales).
Vậy \(BD = \frac{{75}}{7}cm;DC = \frac{{100}}{7}cm;DE = \frac{{60}}{7}cm\).
b) Xét tam giác \(ABC\) có:
\(B{C^2} = {25^2} = 625;A{C^2} = {20^2} = 400;A{B^2} = {15^2} = 225\)
\( \Rightarrow B{C^2} = A{C^2} + A{B^2}\)
Do đó, tam giác\(ABC\) là tam giác vuông tại \(A\).
c) Diện tích tam giác \(ABC\) là
\({S_{ABC}} = \frac{1}{2}AB.AC = \frac{1}{2}.15.20 = 150\left( {c{m^2}} \right)\).
Xét tam giác \(ADB\) và tam giác \(ABC\) ta có:
\(\frac{{BD}}{{BC}} = \frac{{\frac{{75}}{7}}}{{25}} = \frac{3}{7}\) và có chung chiều cao hạ từ đỉnh \(A\). Do đó, diện tích tam giác \(ADB\) bằng \(\frac{3}{7}\) diện tích tam giác \(ABC\).
Diện tích tam giác \(ADB\) là:
\({S_{ADB}} = 150.\frac{3}{7} = \frac{{450}}{7}\left( {c{m^2}} \right)\).
Diện tích tam giác \(ACD\) là:
\({S_{ACD}} = {S_{ABC}} - {S_{ADB}} = 150 - \frac{{450}}{7} = \frac{{600}}{7}\)
Vì \(ED//AB \Rightarrow \frac{{CE}}{{AE}} = \frac{{CD}}{{BD}} = \frac{{\frac{{100}}{7}}}{{\frac{{75}}{{100}}}} = \frac{4}{3}\)
Xét tam giác \(ADE\) và tam giác \(DCE\) ta có:
\(\frac{{CE}}{{AE}} = \frac{4}{3}\) và hai tam giác này có chung đường cao hạ từ \(D\).
Do đó, \(\frac{{{S_{ADE}}}}{{{S_{DCE}}}} = \frac{4}{3}\).
Diện tích tam giác \(ADE\) là
\({S_{ADE}} = \frac{{600}}{7}:\left( {3 + 4} \right).4 = \frac{{2400}}{{49}}\left( {c{m^2}} \right)\)
\({S_{DCE}} = \frac{{600}}{7}:\left( {3 + 4} \right).3 = \frac{{1800}}{{49}}\left( {c{m^2}} \right)\).
Đúng 0
Bình luận (0)
a: Xét ΔABC có AD là phân giác
nên DB/AB=DC/AC
=>DB/3=DC/4=(DB+DC)/(3+4)=25/7
=>DB=75/7cm; DC=100/7cm
Xét ΔABC có DE//AB
nên DE/AB=CD/CB
=>DE/15=100/7:25=4/7
=>DE=60/7cm
b: Xét ΔABC có BC^2=AB^2+AC^2
nen ΔABC vuông tại A
=>S ABC=1/2*15*20=10*15=150cm2
c: DB/DC=3/7
=>S ABD/S ACB=3/7
=>S ABD=150*3/7=450/7cm2
Đúng 0
Bình luận (0)
cho ∆ABC có AB=15cm, AC=20cm và BC=25cm. a) chứng minh : ∆ABC vuông tại A. b) kẻ đường cao AH của ∆ABC. Tính AK, BK và số đo góc C. (làm tròn đến độ) c) gọi M, N lần lượt là hình chiếu của K lên AB, AC. Chứng minh AM.AB=AN.AC. Suy ra ∆AMN đồng dạng với ∆ABC. d) gọi D là trung điểm và I là điểm đối xứng của A qua K. Chứng minh: CD ⊥ IN
Tam giác ABC có AB = 15cm, AC = 20cm, BC = 25cm. Đường phân giác góc BAC cắt cạnh BC tại D. Tính độ dài các đoạn thẳng DB và DC.
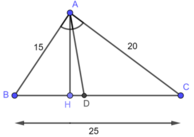
Trong △ ABC, ta có: AD là đường phân giác của (BAC)
Suy ra: ![]() (tính chất đường phân giác)
(tính chất đường phân giác)
Mà AB = 15 (cm); AC = 20 (cm)
Nên ![]()
Suy ra: ![]() (tính chất tỉ lệ thức)
(tính chất tỉ lệ thức)
Suy ra: 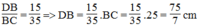
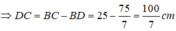
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A có AH là đường cao. Từ H vẽ HD vuông góc với cạnh AB tại D, vẽ hE vuông góc với cạnh AC tại E. Biết AB 15cm, BC 25cm.1)Tính độ dài cạnh AC và diện tích tam giác ABC.2)Chứng minh tứ giác ADHE là hình chữ nhật.3)Trên tia đối của AC lấy điểm F sao cho AF AE. Chứng minh tứ giác AFDH là hình bình hành.4)Gọi K là điểm đối xứng của B qua A, gọi M là trung điểm của AH. Chứng minh CM vuông góc HK.
Đọc tiếp
Cho tam giác ABC vuông tại A có AH là đường cao. Từ H vẽ HD vuông góc với cạnh AB tại D, vẽ hE vuông góc với cạnh AC tại E. Biết AB = 15cm, BC = 25cm.
1)Tính độ dài cạnh AC và diện tích tam giác ABC.
2)Chứng minh tứ giác ADHE là hình chữ nhật.
3)Trên tia đối của AC lấy điểm F sao cho AF = AE. Chứng minh tứ giác AFDH là hình bình hành.
4)Gọi K là điểm đối xứng của B qua A, gọi M là trung điểm của AH. Chứng minh CM vuông góc HK.
1: AC=20cm
\(S_{ABC}=\dfrac{AB\cdot AC}{2}=\dfrac{15\cdot20}{2}=150\left(cm^2\right)\)
2: Xét tứ giác ADHE có
\(\widehat{ADH}=\widehat{AEH}=\widehat{DAE}=90^0\)
Do đó: ADHE là hình chữ nhật
3: Xét tứ giác AFDH có
AF//DH
AF=DH
Do đó: AFDH là hình bình hành
Đúng 0
Bình luận (0)
Cho tam giác ABC có AB=15cm, AC=20cm,BC=25cm. Đường phân giác góc BAC cắt BC tại D
a) tính độ dài DB và DC
b) tính tỉ số diện tích tam giác ABC và tam giác ACD
a) Xét tam giác ABC có:
BD là tia phân giác \(\widehat{BAC}\)
\(\Rightarrow\dfrac{AB}{AC}=\dfrac{BD}{DC}=\dfrac{15}{20}=\dfrac{3}{4}\)(tính chất)
\(\Rightarrow\dfrac{DB}{3}=\dfrac{DC}{4}=\dfrac{DB+DC}{3+4}=\dfrac{BC}{7}=\dfrac{25}{7}\)(tính chất dãy tỉ số bằng nhau)
\(\Rightarrow\left\{{}\begin{matrix}DB=\dfrac{25.3}{7}=\dfrac{75}{7}\left(cm\right)\\DC=\dfrac{25.4}{7}=\dfrac{100}{7}\left(cm\right)\end{matrix}\right.\)
b) Kẻ đường cao AH của tam giác ABC
\(\Rightarrow\dfrac{S_{ACD}}{S_{ABC}}=\dfrac{\dfrac{1}{2}.AH.DC}{\dfrac{1}{2}.AH.BC}=\dfrac{DC}{BC}=\dfrac{100}{7}:25=\dfrac{4}{7}\)
Đúng 1
Bình luận (0)
a: Xét ΔABC có
AD là đường phân giác ứng với cạnh BC
nên \(\dfrac{BD}{AB}=\dfrac{CD}{AC}\)
hay \(\dfrac{BD}{15}=\dfrac{CD}{20}\)
mà BD+CD=25cm
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{BD}{15}=\dfrac{CD}{20}=\dfrac{25}{35}=\dfrac{5}{7}\)
Do đó: \(BD=\dfrac{75}{7}cm;CD=\dfrac{100}{7}cm\)
Đúng 1
Bình luận (0)
Cho tam giác ABC có AB=15cm, AC=20cm,BC=25cm. Đường phân giác góc BAC cắt BC tại D
a) tính độ dài DB và DC
b) tính tỉ số diện tích tam giác ABC và tam giác ACD
Hình tự vẽ lấy nhé
a) Trong tam giác ABC, ta có: AD là đường phân giác của:
\(\Rightarrow\frac{DB}{DC}=\frac{AB}{AC}\)
Mà AB = 15cm và AC = 20cm ( gt )
Nên \(\frac{DB}{DC}=\frac{15}{20}\)
\(\Rightarrow\frac{DB}{DB+DC}=\frac{15}{15+20}\)( Tính chất tỉ lệ thức đã học ở lớp 7 )
\(\Rightarrow\frac{DB}{BC}=\frac{15}{35}\Rightarrow DB=\frac{15}{35}.BC=\frac{15}{35}.25=\frac{75}{7}\left(cm\right)\)
b) Kẻ \(AH\perp BC\)
Ta có: \(S_{ABD}=\frac{1}{2}AH.BD\)
\(S_{ACD}=\frac{1}{2}AH.CD\)
\(\Rightarrow\frac{S_{ABD}}{S_{ACD}}=\frac{\frac{1}{2}AH.BD}{\frac{1}{2}AH.CD}=\frac{BD}{DC}\)
Mà \(\frac{DB}{DC}=\frac{15}{12}=\frac{3}{4}\)
\(\Rightarrow\frac{S_{ABD}}{S_{ACD}}=\frac{3}{4}\left(đpcm\right)\)
Đúng 0
Bình luận (0)
Bài 1 Cho tam giác vuông có số đo hai cạnh góc vuông lần lượt là 3cm và 4cm Hãy tính số đo của các cạnh còn lại
Bài 2 Cho tam giác ABC có cạnh AB dài 25cm Trên cạnh BC lấy hai điểm M N sao cho độ dài đoạn BM bằng 2 phần 6 độ dài BC độ dài đoạn BC = 1,6 độ dài đoạn BC biết chiều cao kẻ từ B của tam giác a m b là 12cm Tìm diện tích hình tam giác ABC tính diện tích hình tam giác amn
Bài 4: Cho Tam Giác ABC Có Đường Cao AH (H Thuộc BC) Và Độ Dài Ba Cạnh Lần Lượt Là AB15CM, BC25CM Và AC20CMBài 5: Cho Hình Thang ABCD Có Đường Cao BH12CM (H Thuộc DC) Và BD15CM. Hai Đường Chéo AC Và BD Vuông Góc Với Nhau. Qua B Vẽ Đường Thẳng Song Song Với AC, Cắt DC Ở E.1) Chứng Minh Rằng Tam Giac BDE Là Tam Giac Vuông 2) Tính Độ Dài Của Các Đoạn Thẳng DH Và De 3) Tính Diện Tích Của Hình Thang ABCD
Đọc tiếp
Bài 4: Cho Tam Giác ABC Có Đường Cao AH (H Thuộc BC) Và Độ Dài Ba Cạnh Lần Lượt Là AB=15CM, BC=25CM Và AC=20CM
Bài 5: Cho Hình Thang ABCD Có Đường Cao BH=12CM (H Thuộc DC) Và BD=15CM. Hai Đường Chéo AC Và BD Vuông Góc Với Nhau. Qua B Vẽ Đường Thẳng Song Song Với AC, Cắt DC Ở E.
1) Chứng Minh Rằng Tam Giac BDE Là Tam Giac Vuông
2) Tính Độ Dài Của Các Đoạn Thẳng DH Và De
3) Tính Diện Tích Của Hình Thang ABCD
5:
1: BE//AC
AC vuông góc BD
=>BE vuông góc BD
=>ΔBED vuông tại B
2:
DH=căn BD^2-BH^2=9cm
ΔBED vuông tại B có BH là đường cao
nên BD^2=DH*DE
=>DE=15^2/9=25cm
BE=căn 25^2-15^2=20(cm)
Đúng 1
Bình luận (0)




