Cho tứ diện đều \(ABCD\). Chứng minh rằng \(AB \bot CD\).
H24
Những câu hỏi liên quan
Cho tứ diện \(ABCD\) có \(\left( {ABD} \right) \bot \left( {BCD} \right)\) và \(CD \bot BD\). Chứng minh rằng tam giác \(ACD\) vuông.
Ta có:
\(\left. \begin{array}{l}\left( {ABD} \right) \bot \left( {BCD} \right)\\\left( {ABD} \right) \cap \left( {BCD} \right) = BD\\C{\rm{D}} \subset \left( {BCD} \right)\\C{\rm{D}} \bot B{\rm{D}}\end{array} \right\} \Rightarrow C{\rm{D}} \bot \left( {ABD} \right) \Rightarrow C{\rm{D}} \bot A{\rm{D}}\)
Vậy tam giác \(ACD\) vuông tại \(D\).
Đúng 0
Bình luận (0)
Cho tứ diện ABCD có \(AB \bot (BCD),BC \bot CD\). Gọi M và N lần lượt là hình chiếu vuông góc của B trên AC và AD. Chứng minh rằng:
a) \(CD \bot BM\)
b, \(BM \bot MN\)
a) Vì \(AB \bot \left( {BCD} \right) \Rightarrow AB \bot CD\)
Mà \(CD \bot BC\)\( \Rightarrow CD \bot \left( {ABC} \right)\)
Lại có \(BM \in \left( {ABC} \right)\)\( \Rightarrow CD \bot BM\)
b) Ta có \(\left. \begin{array}{l}BM \bot CD\\BM \bot AC\end{array} \right\} \Rightarrow BM \bot \left( {ACD} \right)\)
Mà \(MN \in \left( {ACD} \right) \Rightarrow BM \bot MN\)
Đúng 0
Bình luận (0)
Cho tứ diện ABCD có \(AB \bot (BCD)\), các tam giác BCD và ACD là những tam giác nhọn. Gọi H, K lần lượt là trực tâm của các tam giác BCD, ACD (Hình 31). Chứng minh rằng:
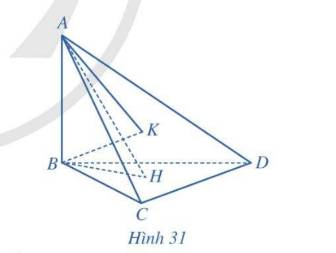
a) \(CD \bot (ABH)\)
b) \(CD \bot (ABK)\)
c) Ba đường thẳng AK, BH, CD cùng đi qua một điểm
a) Vì \(AB \bot \left( {BCD} \right) \Rightarrow AB \bot CD\left( 1 \right)\)
Có H là trực tâm của tam giác BCD \( \Rightarrow BH \bot CD\left( 2 \right)\)
Tử (1) và (2) \( \Rightarrow CD \bot \left( {ABH} \right)\)
b) Vì \(AB \bot \left( {BCD} \right) \Rightarrow AB \bot CD\left( 1 \right)\)
Có K là trực tâm của tam giác BCD \( \Rightarrow AK \bot CD\left( 2 \right)\)
Từ (1) và (2) \( \Rightarrow CD \bot \left( {ABK} \right)\)
Đúng 0
Bình luận (0)
Cho tứ diện ABCD có hai mặt ABC và ABD là các tam giác đều chứng minh rằng AB vuông góc với CD
Gọi M là trung điểm AB
\(\Rightarrow\left\{{}\begin{matrix}CM\perp AB\\DM\perp AB\end{matrix}\right.\) (trong tam giác đều trung tuyến đồng thời là đường cao)
\(\Rightarrow AB\perp\left(CDM\right)\)
\(\Rightarrow AB\perp CD\)
Đúng 0
Bình luận (0)
Cho tứ diện ABCD có các cạnh đều bằng a. Gọi M, N tương ứng là trung điểm của các cạnh AB, CD. Chứng minh rằng:
a) MN là đường vuông góc chung của AB và CD.
b) Các cặp cạnh đối diện trong tứ diện ABCD đều vuông góc với nhau.
Cho tứ diện ABCD. Chứng minh rằng AB vuông góc với CD khi và chỉ khi A C 2 + B D 2 = A D 2 + B C 2
Giả sử AB ⊥ CD ta phải chứng minh:
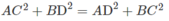
Thật vậy, kẻ BE ⊥ CD tại E, do AB⊥CD ta suy ra CD ⊥ (ABE) nên CD ⊥ AE. Áp dụng định lí Py-ta-go cho các tam giác vuông AEC, BEC, AED và BED ta có:
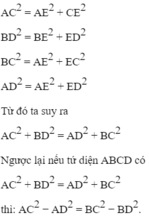
Nếu
A
C
2
−
A
D
2
=
B
C
2
−
B
D
2
=
k
2
thì trong mặt phẳng (ACD) điểm A thuộc đường thẳng vuông góc với CD tại điểm H trên tia ID với I là trung điểm của CD sao cho 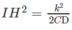
Tương tự điểm B thuộc đường thẳng vuông góc với CD cũng tại điểm H nói trên. Từ đó suy ra CD vuông góc với mặt phẳng (ABH) hay CD ⊥ AB.
Nếu A C 2 − A D 2 = B C 2 − B D 2 = - k 2 thì ta có và đưa về trường hợp xét như trên A C 2 − A D 2 = B C 2 − B D 2 = - k 2 .
Chú ý. Từ kết quả của bài toán trên ta suy ra:
Tứ diện ABCD có các cặp cạnh đối diện vuông góc với nhau khi và chỉ khi A B 2 + C D 2 = A C 2 + B C 2 .
Đúng 0
Bình luận (0)
cho tứ diện đều ABCD chứng minh AB vuông CD bằng phương pháp tích vô hướng
Cho tứ diện ABCD. Chứng minh rằng:
\(\left(AB+CD\right)^2+\left(AD+BC\right)^2>\left(AC+BD\right)^2\)
Cho hình chóp \(S.ABCD\) có \(SA \bot \left( {ABCD} \right)\). Cho biết \(ABCD\) là hình thang vuông tại \(A\) và \({\rm{D}}\), \(AB = 2AD\).
a) Chứng minh \(CD \bot \left( {SAD} \right)\).
b) Gọi \(M\) là trung điểm của \(AB\). Chứng minh \(CM \bot \left( {SAB} \right)\).
tham khảo:

a) Vì SA⊥(ABCD) nên SA⊥CD
Ta có: DC⊥AD;DC⊥SA nên DC⊥(SAD)
b) Vì SA⊥(ABCD) nên SA⊥CM
Ta có: AB = 2CD nên AM = CD. Suy ra AMCD là hình chữ nhật nên CM⊥AB
Mà CM⊥SA
Suy ra: CM⊥(SAB)
Đúng 1
Bình luận (0)



