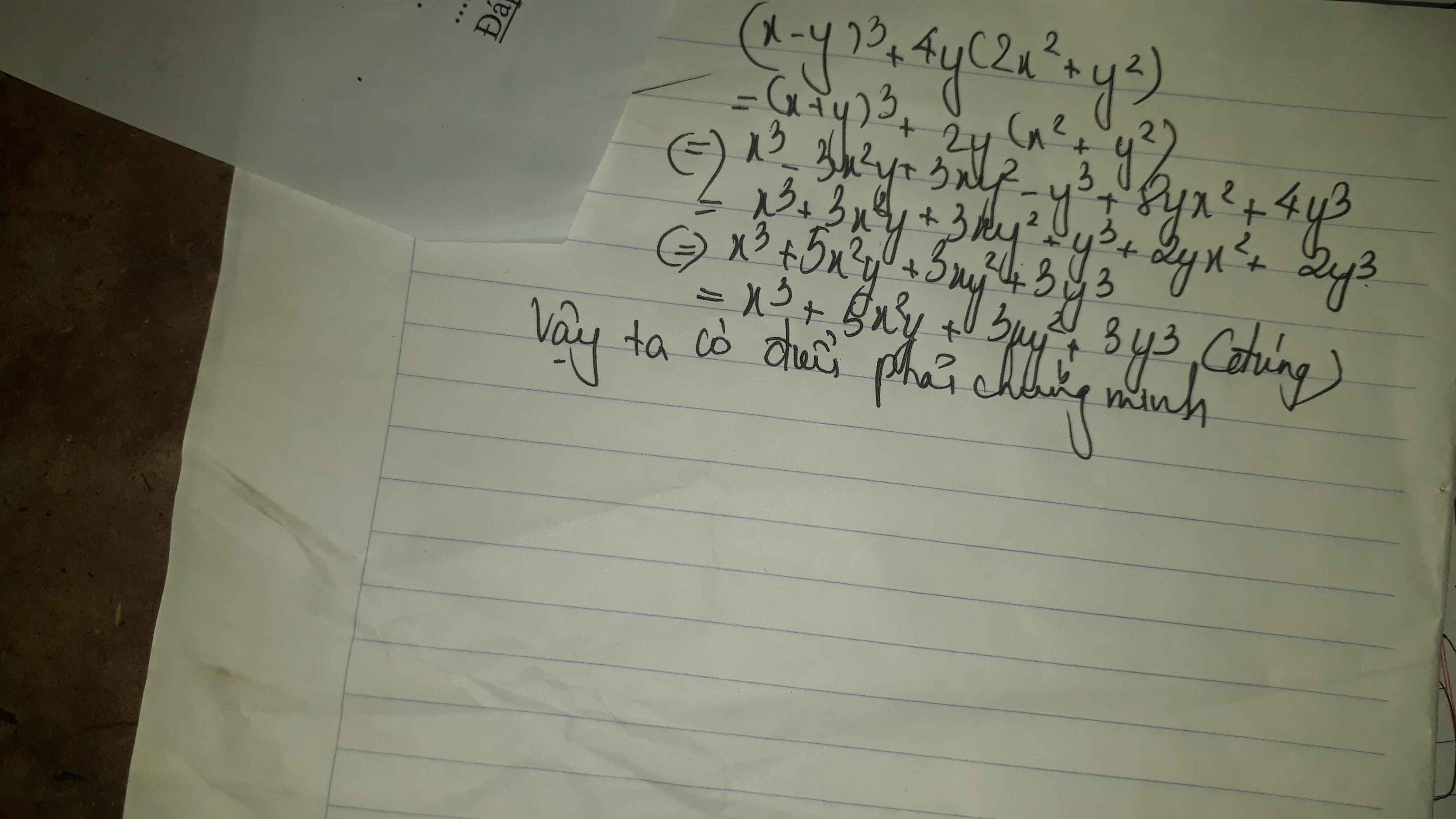chứng minh rắng : (x+y)^2 + (x-y)^2 -2(x-y)(x-y)=4y^2
DT
Những câu hỏi liên quan
chứng minh rắng : (x+y)^2 + (x-y)^2 -2(x+y)(x-y)=4y^2
\((x+y)^2+(x-y)^2-2(x+y)(x-y)\)
\(= x^2 + 2xy + y^2 + x^2 - 2xy + y^2 - 2(x^2 - y^2)\)
\(= (x^2 + x^2) + (2xy - 2xy) + (y^2 + y^2) - 2x^2 + 2y^2\)
\(= 2x^2 + 2y^2 - 2x^2 + 2y^2\)
\(= (2x^2 - 2x^2) + (2y^2 + 2y^2)\)
\(= 4y^2\)
Đúng 1
Bình luận (0)
Chứng minh rắng các biểu thức sau luôn có giá trị dương với mọi giá trị của x:
a/ x^2+x+1
b/ 2x^2+2x+1
c/ x^2+xy+y^2+1
d/x^2+4y^2+z^2-2x-6z+8y+15
a, x2+ x+ 1
= x2 + 2x.1 +12
= ( x+1)2
Có: (x+1)2 >= 0
nên biểu thức luôn dương với mọi gia trị của x
tương tự với các phần còn lại
Đúng 0
Bình luận (0)
Chứng minh rắng các biểu thức sau luôn có giá trị dương với mọi giá trị của x:
a/ x^2+x+1
b/ 2x^2+2x+1
c/ x^2+xy+y^2+1
d/x^2+4y^2+z^2-2x-6z+8y+15
a: \(x^2+x+1\)
\(=x^2+2\cdot x\cdot\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{3}{4}\)
\(=\left(x+\dfrac{1}{2}\right)^2+\dfrac{3}{4}>0\)
b: \(2x^2+2x+1\)
\(=2\left(x^2+x+\dfrac{1}{2}\right)\)
\(=2\left(x^2+x+\dfrac{1}{4}+\dfrac{1}{4}\right)\)
\(=2\left(x+\dfrac{1}{2}\right)^2+\dfrac{1}{2}>0\)
c: \(x^2+xy+y^2+1\)
\(=x^2+2\cdot x\cdot\dfrac{1}{2}y+\dfrac{1}{4}y^2+\dfrac{3}{4}y^2+1\)
\(=\left(x+\dfrac{1}{2}y\right)^2+\dfrac{3}{4}y^2+1>0\)
Đúng 0
Bình luận (0)
Chứng minh rắng các biểu thức sau luôn có giá trị dương với mọi giá trị của x:
a/ x^2+x+1
b/ 2x^2+2x+1
c/ x^2+xy+y^2+1
d/x^2+4y^2+z^2-2x-6z+8y+15
a: \(x^2+x+1\)
\(=x^2+2\cdot x\cdot\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{3}{4}\)
\(=\left(x+\dfrac{1}{2}\right)^2+\dfrac{3}{4}>0\)
b: \(2x^2+2x+1\)
\(=2\left(x^2+x+\dfrac{1}{2}\right)\)
\(=2\left(x^2+x+\dfrac{1}{4}+\dfrac{1}{4}\right)\)
\(=2\left(x+\dfrac{1}{2}\right)^2+\dfrac{1}{2}>0\)
c: \(x^2+xy+y^2+1\)
\(=x^2+2\cdot x\cdot\dfrac{1}{2}y+\dfrac{1}{4}y^2+\dfrac{3}{4}y^2+1\)
\(=\left(x+\dfrac{1}{2}y\right)^2+\dfrac{3}{4}y^2+1>0\)
Đúng 0
Bình luận (0)
Chứng minh rắng các biểu thức sau luôn có giá trị dương với mọi giá trị của x:
a/ x^2+x+1
b/ 2x^2+2x+1
c/ x^2+xy+y^2+1
d/x^2+4y^2+z^2-2x-6z+8y+15
chứng minh đẳng thức (x-y)^3+4y(2x^2+y^2)=(x+y)^3+2y(x^2+y^2)
Ta có: \(\left(x-y\right)^3+4y\left(2x^2+y^2\right)\)
\(=x^3-3x^2y+3xy^2-y^3+8x^2y+4y^3\)
\(=x^3+5x^2y+3xy^2+3y^3\)
\(=x^3+3x^2y+3xy^2+y^3+2x^2y+2y^3\)
\(=\left(x+y\right)^3+2y\left(x^2+y^2\right)\)
Đúng 0
Bình luận (0)
chứng minh các đẳng thức sau (x-y)^3 +4y(2x^2+y^2)=(x+y)^3+2y(x^2+y^2)
\(\left(x-y\right)^3+4y\left(2x^2+y^2\right)=\left(x+y\right)^3+2y\left(x^2+y^2\right)\)
\(\Leftrightarrow x^3-3x^2y+3xy^2-y^3+8x^2y+4y^3=x^3+3x^2y+3xy^2+y^3+2x^2y+2y^3\)
\(\Leftrightarrow\left(-3x^2y+8x^2y\right)+3xy^2+3y^3=\left(3x^2y+2x^2y\right)+3xy^2+3y^2\)
\(\Leftrightarrow5x^2y+3xy^2+3y^2=5x^2y+3xy^2+3y^2\)
Đúng 0
Bình luận (0)
Cho x,y \(\in Z\) chứng minh rắng:
\(N=\left(x-y\right)\left(x-2y\right)\left(x-3y\right)\left(x-4y\right)+y^4\) là số chính phưang
\(\Leftrightarrow N=\left[\left(x-y\right)\left(x-4y\right)\right]\left[\left(x-2y\right)\left(x-3y\right)\right]+y^4\)
\(\Leftrightarrow N=\left(x^2+4y^2-5xy\right)\left(x^2-5xy+6y^2\right)+y^4\)
Đặt \(t=x^2+4y^2-5xy\)
Khi đó
\(N=t\left(t+2y^2\right)+y^4=t^2+2ty^2+\left(y^2\right)^2=\left(y^2+t\right)^2=\left(x^2-5xy+5y^2\right)^2\)
=> N là số chính phương
x,y nguyên dương thoả mãn x^2+y^2+4=2xy+4x+4y .chứng minh x/2 và y/2 là các số chính phương
\(x^2+y^2+4=2xy+4x+4y\)
\(\Leftrightarrow x^2-\left(2y+4\right)x+y^2-4y+4=0\)
Xét phương trình theo nghiệm x.
\(\Rightarrow\Delta'=\left(y+2\right)^2-\left(y^2-4y+4\right)=8y\)
\(\Rightarrow\orbr{\begin{cases}x=y+2-2\sqrt{2y}\\x=y+2+2\sqrt{2y}\end{cases}}\)
Vì x, y nguyên dương nên
\(\Rightarrow\sqrt{2y}=a\)
\(\Rightarrow y=2n^2\)
\(\Rightarrow\orbr{\begin{cases}x=2n^2+2-4n\\x=2n^2+2+4n\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x=2\left(n-1\right)^2\\x=2\left(n+1\right)^2\end{cases}}\)
Vậy \(\frac{y}{2};\frac{x}{2}\)là 2 số chính phương.
Đúng 0
Bình luận (0)
\(x^2+y^2+4=2xy+4x+4y\)
<=> \(\left(x^2-4x+4\right)+y^2-2y\left(x-2\right)=8y\)
<=> \(\left(x-y-2\right)^2=8y\)
<=> \(\left(\frac{x-y-2}{4}\right)^2=\frac{y}{2}\)
=> \(\frac{y}{2}\)là số chính phương
CMTT x/2 là số chính phương
Đúng 0
Bình luận (0)