Tính giá trị các biểu thức sau:
a) \({\log _2}16\);
b) \({\log _3}\frac{1}{{27}}\);
c) \(\log 1000\);
d) \({9^{{{\log }_3}12}}\).
Tính giá trị của các biểu thức sau:
a) \(A = {\log _2}3.{\log _3}4.{\log _4}5.{\log _5}6.{\log _6}7.{\log _7}8;\)
b) \(B = {\log _2}2.{\log _2}4...{\log _2}{2^n}.\)
\(a,A=log_23\cdot log_34\cdot log_45\cdot log_56\cdot log_67\cdot log_78\\ =log_28\\ =log_22^3\\ =3\\ b,B=log_22\cdot log_24...log_22^n\\ =log_22\cdot log_22^2...log_22^n\\ =1\cdot2\cdot...\cdot n\\ =n!\)
Tính giá trị các biểu thức sau:
a) \({\log _2}9.{\log _3}4\);
b) \({\log _{25}}\frac{1}{{\sqrt 5 }}\);
c) \({\log _2}3.{\log _9}\sqrt 5 .{\log _5}4\).
a) \(log_29\cdot log_34=4\)
b) \(log_{25}\cdot\dfrac{1}{\sqrt{5}}=-\dfrac{1}{4}\)
c) \(log_23\cdot log_9\sqrt{5}\cdot log_54=\dfrac{1}{2}\)
a) Tính \(y = {\log _2}x\) khi x lần lượt nhận các giá trị 1; 2; 4. Với mỗi giá trị của x > 0 có bao nhiêu giá trị của \(y = {\log _2}x\) tương ứng?
b) Với những giá trị nào của x, biểu thức \(y = {\log _2}x\) có nghĩa?
a) Với \(x = 1\) thì \(y = {\log _2}1 = 0\)
Với \(x = 2\) thì \(y = {\log _2}2 = 1\)
Với \(x = 4\) thì \(y = {\log _2}4 = 2\)
b) Biểu thức \(y = {\log _2}x\) có nghĩa khi x > 0.
Tính giá trị các biểu thức sau:
a) \({\log _{\frac{1}{4}}}8\);
b) \({\log _4}5.{\log _5}6.{\log _6}8\).
a: \(log_{\dfrac{1}{4}}8=log_{2^{-2}}2^3=\dfrac{-3}{2}\cdot log_22=-\dfrac{3}{2}\)
b: \(log_45\cdot log_56\cdot log_68\)
\(=log_45\cdot\dfrac{log_46}{log_45}\cdot\dfrac{log_48}{log_46}\)
\(=log_48=log_{2^2}2^3=\dfrac{3}{2}\)
Tính giá trị các biểu thức sau:
a) \({\log _6}9 + {\log _6}4\);
b) \({\log _5}2 - {\log _5}50\);
c) \({\log _3}\sqrt 5 - \frac{1}{2}{\log _3}15\).
a) \(log_69+log_64=log_636=2\)
b) \(log_52-log_550=log_5\left(2:50\right)=-2\)
c) \(log_3\sqrt{5}-\dfrac{1}{2}log_550=-1,0479\)
Cho hàm số lôgarit \(y = {\log _2}x\)
a) Tìm giá trị y tương ứng với giá trị của x trong bảng sau: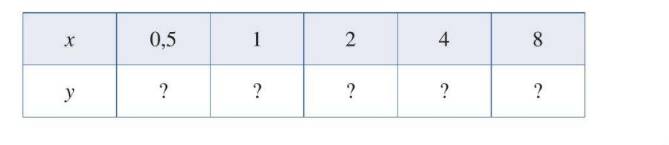
b, Trong mặt phẳng tọa độ Oxy, biểu diễn các điểm (x; y) trong bảng giá trị ở câu a.
Bằng cách làm tương tự, lấy nhiều điểm \(\left( {x;{{\log }_2}x} \right)\) với \(x \in (0; + \infty )\) và nối lại ta được đồ thị hàm số \(y = {\log _2}x\) như hình bên.
c, Cho biết tọa độ giao điểm của đồ thị hàm số \(y = {\log _2}x\) với trục hoành và vị trí của đồ thị hàm số đó với trục tung.
d, Quan sát đồ thị hàm số \(y = {\log _2}x\), nêu nhận xét về:
\(\mathop {\mathop {\lim }\limits_{x \to {0^ + }} ({{\log }_2}x)}\limits_{} \,;\mathop {\,\,\mathop {\lim }\limits_{x \to + \infty } ({{\log }_2}x)}\limits_{} \)Sự biến thiên của hàm số \(y = {\log _2}x\) và lập bảng biến thiên của hàm số đóa:
| x | 0,5 | 1 | 2 | 4 | 8 |
| \(y\) | -1 | 0 | 1 | 2 | 3 |
b:
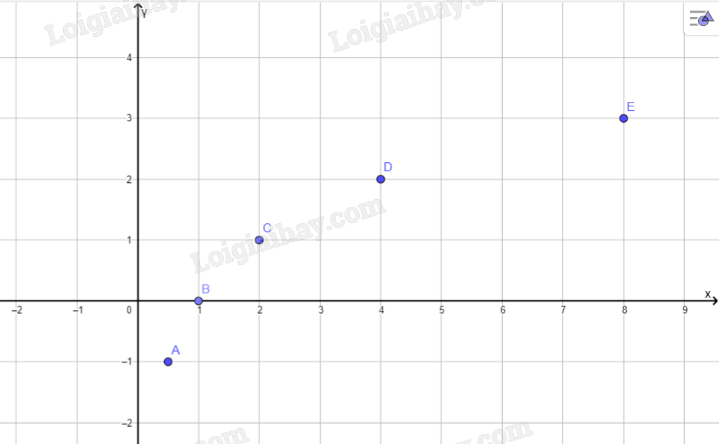
c: Tọa độ giao điểm của hàm số với trục hoành là B(2;0)
Đồ thị hàm số này ko cắt trục tung
d:
\(\lim\limits_{x\rightarrow0^+}log_2x=0\)
\(\lim\limits_{x\rightarrow+\infty}\left(log_2x\right)=+\infty\)
=>Hàm số này đồng biến trên TXĐ của nó là D=[0;+vô cực)

Giải các phương trình sau:
a) \(4 - \log \left( {3 - x} \right) = 3;\)
b) \({\log _2}\left( {x + 2} \right) + {\log _2}\left( {x - 1} \right) = 1.\)
tham khảo
a)Điều kiện \(3-x>0\) hay \(x< 3\)
\(4-log\left(3-x\right)=3log\left(3-x\right)=1\Leftrightarrow10^1=3-x\)
Vậy nghiệm của phương trình là \(x=2\) thỏa mãn điều kiện
b) Điều kiện \(x+2>0\) và \(x-1>0\) tức là \(x>1\)
\(\left(x+2\right)\left(x-1\right)=2\Rightarrow x^2+x-4=0\)
Vậy pt có nghiệm \(x=\dfrac{-1+\sqrt{17}}{2}\)
Cho hàm số lôgarit \(y = {\log _2}x.\)
a) Hoàn thành bảng giá trị sau:

b) Trong mặt phẳng tọa độ Oxy, biểu diễn các điểm (x; y) trong bảng giá trị ở câu a. Bằng cách làm tương tự, lấy nhiều điểm \(\left( {x;{{\log }_2}x} \right)\) với \(x \in \mathbb{R}\) và nối lại ta được đồ thị của hàm số \(y = {\log _2}x\)
c) Từ đồ thị đã vẽ ở câu b, hãy kết luận về tập giá trị và tính chất biến thiên của hàm số \(y = {\log _2}x\)
Giải các phương trình sau:
a) \({\log _{\frac{1}{2}}}\left( {x - 2} \right) = - 2\);
b) \({\log _2}\left( {x + 6} \right) = {\log _2}\left( {x + 1} \right) + 1\)
a) \({\log _{\frac{1}{2}}}\left( {x - 2} \right) = - 2\)
Điều kiện: \(x - 2 > 0 \Leftrightarrow x > 2\)
Vậy phương trình có nghiệm là \(x = 6\).
b) \({\log _2}\left( {x + 6} \right) = {\log _2}\left( {x + 1} \right) + 1\)
Điều kiện: \(\left\{ \begin{array}{l}x + 6 > 0\\x + 1 > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x > - 6\\x > - 1\end{array} \right. \Leftrightarrow x > - 1\)
Vậy phương trình có nghiệm là \(x = 4\).