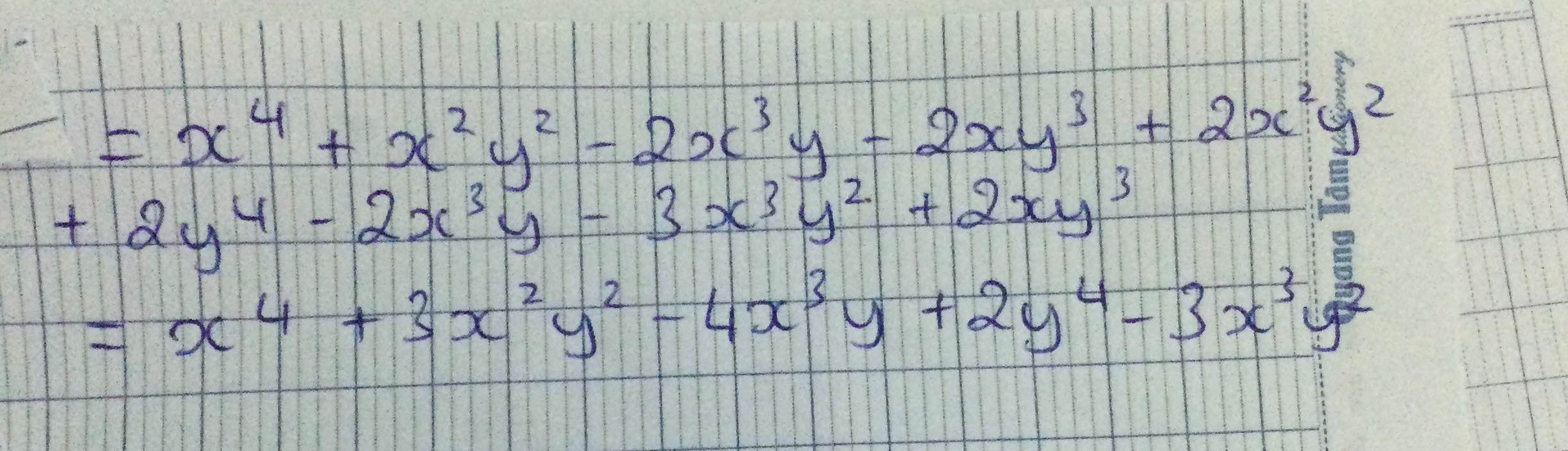2x2(x2+y2)+2y2(x2+y2)+5 (y2+x2) với x2+y2=1
TH
Những câu hỏi liên quan
2x2(x2+y2)+2y2(x2+y2)+5 (y2+x2) với x2+y2=1
\(2x^2\left(x^2+y^2\right)+2y^2\left(x^2+y^2\right)+5\left(y^2+x^2\right)\)
\(=\left(x^2+y^2\right)\left(2x^2+2y^2\right)+5\left(x^2+y^2\right)\)
\(=2\left(x^2+y^2\right)\left(x^2+y^2\right)+5\left(x^2+y^2\right)\)
\(=2\left(x^2+y^2\right)^2+5\left(x^2+y^2\right)\)
Thay \(x^2+y^2=1\) vào ta có:
\(2\cdot1^2+5\cdot1=2+5=7\)
Đúng 2
Bình luận (0)
Phương trình nào sau đây là phương trình của đường tròn? (I) x2+ y2 – 4x +15y -12 0. (II) x2+ y2 – 3x +4y +20 0. (III) 2x2+ 2y2- 4x + 6y +1 0 . A. Chỉ (I). B. Chỉ (II). C. Chỉ (III). D. Chỉ (I) và (III).
Đọc tiếp
Phương trình nào sau đây là phương trình của đường tròn?
(I) x2+ y2 – 4x +15y -12= 0.
(II) x2+ y2 – 3x +4y +20= 0.
(III) 2x2+ 2y2- 4x + 6y +1= 0 .
A. Chỉ (I).
B. Chỉ (II).
C. Chỉ (III).
D. Chỉ (I) và (III).
Ta xét các phương án:
(I) có:
![]()
(II) có:
![]()
(III) tương đương : x2+ y2 – 2x - 3y + 0,5= 0.
phương trình này có:
![]()
Vậy chỉ (I) và (III) là phương trình đường tròn.
Chọn D.
Đúng 0
Bình luận (0)
tìm GTNN của các bt
a, A=2x2+y2-2xy-2x+3
b,B=x2-2xy+2y2+2x-10y+17
c,C=x2-xy+y2-2y-2x
d,D=x2+xy+y2-3y-3x
e,E=2x2+2xy +5y2-8x-22y
A= 2x^2 + y^2 - 2xy -2x+3
A= x^2-2xy + y^2 + x^2 - 2x+ 1 +2
A= (x-y)^2 + (x-1)^2 + 2
(x-y)^2> hoặc = 0 với mọi giá trị của x
(x-1)^2 > hoặc =0 với mọi giá trị của x
=> (x-y)^2 + (x-1)^2 > hoặc =0 với mọi giá trị của x
=> (x-y)^2 + (x-1)^2 + 2 > hoặc =2
=> A lớn hơn hoặc bằng 2
=> GTNN của A=2 tại x=y=1
Đúng 0
Bình luận (0)
bài 1: cho các số dương x, y, z thỏa mãn x+y+z=1. Tìm min
a) A = x2+y2+z2
b) B = x2+y2+3z2
c) C=x2+2y2+3z2
d) D=x2+by2+cz2
b1 cho hai đại lượng tỉ lệ nghịch x và y, x1 và x2 là 2 giá trị của x, y1,y2 là 2 giá trị của y a)biết x15,x22 và y1+y221. tính y1 và y2b)biết x2 -4,y1-10và 3x1-2y232.tính x1 và y2b2 cho hai đại lượng tỉ lệ nghịch x và y, x1 và x2 là hai giá trị của x, y1 và y2 là hai giá trị tương ứng của y: a) Biết x13, x22 và 2y1+3y2-26. Tính y1 và y2.b) Biết x2-4, y1-10 và 3x1-2y232. Tính x1 và y2.giúp mình với nhé các bạn
Đọc tiếp
b1 cho hai đại lượng tỉ lệ nghịch x và y, x1 và x2 là 2 giá trị của x, y1,y2 là 2 giá trị của y a)biết x1=5,x2=2 và y1+y2=21. tính y1 và y2
b)biết x2 =-4,y1=-10và 3x1-2y2=32.tính x1 và y2
b2 cho hai đại lượng tỉ lệ nghịch x và y, x1 và x2 là hai giá trị của x, y1 và y2 là hai giá trị tương ứng của y: a) Biết x1=3, x2=2 và 2y1+3y2=-26. Tính y1 và y2.
b) Biết x2=-4, y1=-10 và 3x1-2y2=32. Tính x1 và y2.
giúp mình với nhé các bạn
cảm ơn các bạn trước
tìm đa thức B và tính giá trị của đa thức B tại x=1; y=-1/3 biết:
x2-2y2+2/3 x2 y3+B = 2x2+y2+2/3 x2 y3
`x^2-2y^2+2/3x^2y^3+B=2x^2+y^2+2/3x^2y^3`
`=>B=2x^2+y^2+2/3x^2y^3-x^2+2y^2-2/3x^2y^3`
`=>B=(2x^2-x^2)+(y^2+2y^2)+(2/3x^2y^3-2/3x^2y^3)`
`=>B=x^2+3y^2`
Thay `x=1 ; y=[-1]/3` vào `B` có:
`B=1^2+3.([-1]/3)^2=1+3 . 1/9=1+1/3=4/3`
Đúng 4
Bình luận (0)
`x^2 - 2y^2 + 2/3x^2y^3 + B = 2x^2 + y^2 + 2/3x^2y^3`
`=> B = 2x^2 + y^2 + 2/3x^2y^3` `- (x^2 - 2y^2 + 2/3x^2y^3)`
`= 2x^2 + y^2 + 2/3x^2y^3 - x^2 + 2y^2 - 2/3x^2y^3`
`= ( 2x^2 - x^2 ) + ( y^2 + 2y^2 ) + ( 2/3x^2y^3 - 2/3x^2y^3 )`
`= x^2 + 3y^2`
Thay `x=1 ; y=-1/3` vào `B` ta có `:`
`B = 1^2 + 3 . ( -1/3 )^2`
`= 1 + 1/3`
`= 4/3`
Đúng 2
Bình luận (0)
C=(x2-2xy+2y2)(x2+y2)-2x3y-3x3y2+2xy3
giúp mìk với
\(C=\left(x^2-2xy+y^2\right)\left(x^2+y^2\right)-2x^3y-3x^3y^2+2xy^3\)
\(=\left(x^2+y^2\right)^2-2xy\left(x^2+y^2\right)-xy\left(2x^2+3x^2y+2y^2\right)\)
\(=\left(x^2+y^2\right)^2-xy\left(2x^2+2y^2+2x^2+3x^2y+2y^2\right)\)
\(=\left(x^2+y^2\right)^2-xy\left(4x^2+3x^2y+4y^2\right)\)
Đúng 0
Bình luận (0)
Tìm giá trị nhỏ nhất:
a/ P=x2+y2-6x-2y+17
b/ Q=x2+xy+y2-3x-3y+999
c/ R=2x2+2xy+y2-2x+2y+15
d/ S=x2+26y2-10xy+14x-76y+59
e/ T=x2-4xy+5y2+10x-22y+28
Giúp mình với nha!