Tam giác abc nhọn. Góc a = 60 độ . Đường cao ce và bd. Cm: Sade=1/4 Sabc
QN
Những câu hỏi liên quan
Cho tam giác nhọn ABC, hai đường cao BD và CE, Sade = 3/4 Sabc. Tính Â
TA CÓ \(\Delta ADB\)đồng dạng \(\Delta AEC\)(g-g)
\(\Rightarrow\)\(\frac{AD}{AB}=\frac{AE}{AC}\)
Xét \(\Delta AED\)và \(\Delta ACB\) có :
góc A chung
\(\frac{AD}{AB}=\frac{AE}{AC}\)(CMT)
\(\Rightarrow\Delta AED\infty\Delta ACB\)(c-g-c)
\(\frac{S\Delta AED}{S\Delta ACB}=\left(\frac{AD}{AB}\right)^2\)=\(\frac{3}{4}\)
\(\Rightarrow\frac{AD}{AB}=\frac{\sqrt{3}}{2}\)
\(\Rightarrow\cos A=\frac{\sqrt{3}}{2}\)
\(\Rightarrow\)góc A=60 ĐỘ
Đúng 0
Bình luận (0)
cảm ơn bạn nhiều nha!!!!!!!!!!!!!!!!
Đúng 0
Bình luận (0)
Cho tam giác ABC, hai đường cao BD và CE
a. Chứng minh: AE.AB=AD.ACb. Chứng minh: góc ADE=ABC; góc AED=ABCc. Biết Â=60 độ, SABC= 120 cm\(^2\).Tính SADE?hế lô chào mk các streamer
Bài 11. Cho tam giác ABC, các đường cao BD và CE cắt nhau tại H.
a) Chứng minh rằng AE - AB = AD.AC.
b) Chứng minh rằng ADE = ABC.
c) Chứng minh rằng CH - CE+BH - BD = BC.
d) Giả sử góc A có số do bằng 60°, SABC = 120 cm. Tính SADE.
Bài 11. Cho tam giác ABC, các đường cao BD và CE cắt nhau tại H.
a) Chứng minh rằng AE - AB = AD.AC.
b) Chứng minh rằng ADE = ABC.
c) Chứng minh rằng CH - CE+BH - BD = BC.
d) Giả sử góc A có số do bằng 60°, SABC = 120 cm. Tính SADE.
a: Xét ΔADB vuông tại D và ΔAEC vuông tại E có
góc A chung
=>ΔADB đồng dạng với ΔAEC
=>AD/AE=AB/AC
=>AD*AC=AB*AE;AD/AB=AE/AC
b: Xét ΔADE và ΔABC có
AD/AB=AE/AC
góc DAE chung
=>ΔADE đồng dạng với ΔABC
=>góc ADE=góc ABC
d: ΔADE đồng dạngvới ΔABC
=>\(\dfrac{S_{ADE}}{S_{ABC}}=\left(\dfrac{AD}{AB}\right)^2=\dfrac{1}{4}\)
=>\(S_{ADE}=30\left(cm^2\right)\)
Đúng 0
Bình luận (0)
Cho Tam giác ABC, cho 2 đường cao BD,CE giả sử góc BAC = 60 độ thì tỉ số Sade/Sabc là bao nhiêu ?
Cần gấp giải thích kĩ nha
Vì \(\widehat{BAC}=60^o\) nên \(\dfrac{AD}{AB}=\dfrac12\) (sẽ giải thích ở phần sau)
Xét tam giác ABD vuông tại D và tam giác ACE vuông tại E có:
\(\widehat{A}\) là góc chung
Nên \(\triangle ACE \backsim \triangle ABD (g.g) \text{theo tỉ số đồng dạng } k=\dfrac{AD}{AB}=\dfrac12\)
\(=> \dfrac{S_{\triangle{ADE}}}{S_{\triangle{ABC}}} = k^2=(\dfrac12)^2=\dfrac14\)
Vậy \( \dfrac{S_{\triangle{ADE}}}{S_{\triangle{ABC}}} = \dfrac14\)
Bình luận: Vì sao \(\dfrac{AD}{AB}=\dfrac12\)?
Chứng minh điều này như sau:
Kẻ đường trung tuyến DM của tam giác ABD.
Từ đây suy ra \(MD=\dfrac12 AB\) (định lý đường trung tuyến trong tam giác vuông)
Mà \(AM=\dfrac12 AB\) (do DM là trung tuyến)
Nên \(AM=MD\)
Do đó tam giác AMD cân tại M
Mà \(\widehat{MAD}=60^o\) (do \(\widehat{BAC}=60^o\))
Nên tam giác AMD đều
\(=>AM=AD\)
\(=>\dfrac{1}{2}AB=AD\) (DM trung tuyến)
\(=>\dfrac{AD}{AB}=\dfrac{1}{2}=>đpcm\)
Đúng 0
Bình luận (0)
Vì \(\widehat{BAC}=60^o\) nên \(\dfrac{AD}{AB}=\dfrac12\) (sẽ giải thích ở phần sau)
Xét tam giác ABD vuông tại D và tam giác ACE vuông tại E có:
\(\widehat{A}\) là góc chung
Nên \(\triangle ACE \backsim \triangle ABD (g.g)\)
Từ đó tự suy ra \(\triangle ADE \backsim \triangle ABC (c.g.c) \text{ theo tỉ số đồng dạng }k=\dfrac{AD}{AB}=\dfrac12\)
\(=> \dfrac{S_{\triangle{ADE}}}{S_{\triangle{ABC}}} = k^2=(\dfrac12)^2=\dfrac14\)
Vậy \( \dfrac{S_{\triangle{ADE}}}{S_{\triangle{ABC}}} = \dfrac14\)
Bình luận: Vì sao \(\dfrac{AD}{AB}=\dfrac12\)?
Chứng minh điều này như sau:
Kẻ đường trung tuyến DM của tam giác ABD.
Từ đây suy ra \(MD=\dfrac12 AB\) (định lý đường trung tuyến trong tam giác vuông)
Mà \(AM=\dfrac12 AB\) (do DM là trung tuyến)
Nên \(AM=MD\)
Do đó tam giác AMD cân tại M
Mà \(\widehat{MAD}=60^o\) (do \(\widehat{BAC}=60^o\))
Nên tam giác AMD đều
\(=>AM=AD\)
\(=>\dfrac{1}{2}AB=AD\) (DM trung tuyến)
\(=>\dfrac{AD}{AB}=\dfrac{1}{2}=>đpcm\)
Đúng 0
Bình luận (0)
Cho tam giác ABC có ba góc nhọn các đường cao BD, CE cắt nhau tại H
a/Chứng minh : DABD ~ DACE và AD.AC = AE.AB
b/ Chứng minh: góc ade = góc abc
c/ Cho biết góc bac= 60 độ. Tính Sade/Sabc
d/ AH cắt BC tại F. Chứng minh Sade/Sabc
giúp mk câu d vs ạ
a: Xét ΔABD vuông tại D và ΔACE vuông tại E có
\(\widehat{BAD}\) chung
Do đó:ΔABD\(\sim\)ΔACE
Suy ra: AB/AC=AD/AE
hay \(AB\cdot AE=AD\cdot AC\)
b: Xét ΔADE và ΔABC có
AD/AB=AE/AC
\(\widehat{DAE}\) chung
Do đó:ΔADE\(\sim\)ΔABC
Suy ra: \(\widehat{ADE}=\widehat{ABC}\)
Đúng 0
Bình luận (1)
Cho tam giác ABC, hai đường cao BD và CEa. Chứng minh AE.AB AD.ACb. Chứng minh góc ADE ABC góc AED ABCc. Biết  60 độ, SABC 120 cm2.Tính SADE
tam giác ABC nhọn đường cao BD và CE
a, Chứng minh: tam giác ADB đồng dạng với tam giác AEC.
b, Chứng minh: Góc ADE= góc ABC.
c, Biết BAC=60 độ. Tính \(\frac{SABE}{SABC}\)
Cho tam giác nhọn ABC, hai đường cao BD và CE. Chứng minh S A D E = S A B C . cos 2 A
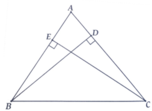
Ta có: ∆ABD ~ ∆ACE( g.g) => A D A B = A E A C
=> S A D E S A B C = A E A C 2
Mà trong ∆ACE có cosA = A E A C
=> S A D E S A B C = cos A 2
=> S A D E = S A B C . cos 2 A
Đúng 0
Bình luận (0)



