Tìm m để phương trình có nghiệm duy nhất
(m2-3m+2)x+3=3m
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
Tìm điều kiện của m để phương trình (3m – 4)x + m = 3 m 2 + 1 có nghiệm duy nhất.
A. m ≠ 4 3
B. x = 4 3
C. m = 4 3
D. m ≠ 3 4
Bài 7. Cho phương trình bậc hai: x2 + 2(m+1)x + m2 - 3m = 0
a. Tìm m để phương trình có nghiệm bằng -1 .
b. Tìm m để phương trình có hai nghiệm phân biệt.
c. Tìm m để phương trình có nghiệm duy nhất
\(a,x=-1\\ \Leftrightarrow1-2\left(m+1\right)+m^2-3m=0\\ \Leftrightarrow-1-5m+m^2=0\\ \Leftrightarrow m^2-5m-1=0\\ \Delta=25+4=29\\ \Leftrightarrow\left[{}\begin{matrix}m=\dfrac{5+\sqrt{29}}{2}\\m=\dfrac{5-\sqrt{29}}{2}\end{matrix}\right.\)
\(b,\)Pt có 2 nghiệm phân biệt
\(\Leftrightarrow\Delta=\left[2\left(m+1\right)\right]^2-4\left(m^2-3m\right)>0\\ \Leftrightarrow4m^2+8m+4-4m^2+12m>0\\ \Leftrightarrow20m+4>0\Leftrightarrow m>-\dfrac{1}{5}\)
\(c,\)Để pt có nghiệm duy nhất (nghiệm kép)
\(\Leftrightarrow\Delta=\left[2\left(m+1\right)\right]^2-4\left(m^2-3m\right)=0\\ \Leftrightarrow20m+4=0\\ \Leftrightarrow m=-\dfrac{1}{5}\)
Số nguyên dương nhỏ nhất của m để phương trình (3m – 3)x + m = 3 m 2 + 1 có nghiệm duy nhất là:
A. m ≠ 1
B. m = 1
C. m = 2
D. m = 0
Tìm tất cả các giá trị của tham số thực m để phương trình m 2 - 3 m + 2 x + m - 1 = 0 có nghiệm thực duy nhất.
A. m ≠ 1 m ≠ 2
B. m ≠ 1
C. m ≠ 2
D. m ≠ 1 hoặc m ≠ 2
Chọn đáp án A
Phương trình đã cho có nghiệm duy nhất khi và chỉ khi 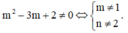
tìm m để phương trình sau có nghiệm duy nhất
m(4mx - 3m +2) = x(m+1)
Bài 6: Cho phương trình m2(x – m) = x – 3m + 2 (*)
a, Tìm m để (*) là phương trình bậc nhất một ẩn
b, Giải PT khi m = 0
c, Tìm m để (1) có nghiệm x = 3
d, Tìm m nguyên để x nguyên
a: =>m^2x-m^3-x+3m-2=0
=>x(m^2-1)=m^3-3m+2
=>x(m-1)(m+1)=m^3-m-2m+2=m(m-1)(m+1)-2(m-1)=(m-1)^2*(m+2)
Để đây là pt bậc nhất 1 ẩn thì (m-1)(m+1)<>0
=>m<>1 và m<>-1
b: Khi m=0 thì pt sẽ là x+2=0
=>x=-2
c: Khi x=3 thì pt sẽ là:
3(m^2-1)=m^3-3m+2
=>(m-1)^2(m+1)-3(m-1)(m+1)=0
=>(m-1)(m+1)(m-1-3)=0
=>(m-1)(m+1)(m-4)=0
=>\(m\in\left\{1;-1;4\right\}\)
Tìm tổng các giá trị của m để phương trình ( m – 2 ) x 2 – ( m 2 + 1 ) x + 3 m = 0 có nghiệm x = −3
A. −5
B. −4
C. 4
D. 6
Thay x = −3 vào phương trình
(m – 2)x2 – (m2 + 1)x + 3m = 0, ta có:
(m – 2) (−3)2 – (m2 + 1) (−3) + 3m = 0
⇔ 9m – 18 + 3m2 + 3 + 3m = 0
⇔ 3m2 + 12m – 15 = 0
⇔ m2 + 4m – 5 = 0
⇔ m2 – m + 5m – 5 = 0
⇔ m (m – 1) + 5 (m – 1) = 0
⇔ (m – 1) (m + 5) = 0 ⇔ m = 1 m = − 5
Suy ra tổng các giá trị của m là (−5) + 1 = −4
Đáp án cần chọn là: B
Cho phương trình : m(m-1)x=m^2+3m+2(x+1)
Tìm m để phương trìh có nghiệm duy nhất thỏa mãn x<1
Cho phương trình : m(m-1)x=m^2+3m+2(x+1)
Tìm m để phương trìh có nghiệm duy nhất thỏa mãn x<1