cho em hỏi hàm số y=ln(-x2+16) đồng biến khoảng nào
0
PT
Những câu hỏi liên quan
Cho hàm số
y
x
2
+
sin
2
x
,
x
∈
0
;
π
. Hỏi hàm số đồng biến trên các khoảng nào?
Đọc tiếp
Cho hàm số y = x 2 + sin 2 x , x ∈ 0 ; π . Hỏi hàm số đồng biến trên các khoảng nào?
Hỏi hàm số
y
ln
(
x
2
+
x
+
2
)
nghịch biến trên khoảng nào A.
(
-
∞
;
-
1
2
)
B.
(
1
2
;
+
∞
)
C.
(
-
1...
Đọc tiếp
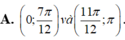
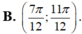
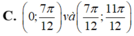
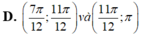
Hỏi hàm số y = ln ( x 2 + x + 2 ) nghịch biến trên khoảng nào
A. ( - ∞ ; - 1 2 )
B. ( 1 2 ; + ∞ )
C. ( - 1 2 ; + ∞ )
D. ( - ∞ ; 1 2 )
Cho bốn hàm số sau : y f(x) lnx ;
y
g
(
x
)
2
x
2
+
4
;
y
h
(
x
)
2017
1018
x
và y l(x) ln( x2+1). Có bao nhiêu hàm số...
Đọc tiếp
Cho bốn hàm số sau : y= f(x) = lnx ; y = g ( x ) = 2 x 2 + 4 ; y = h ( x ) = 2017 1018 x và
y= l(x)= ln( x2+1). Có bao nhiêu hàm số đồng biến trên khoảng ( 0 ; + ∞ )
A. 1
B. 2
C. 3
D. 4
+ Sử dụng tính chất: Hàm số y= logax đồng biến trên TXĐ khi a> 1nên y= f(x) = lnx
là hàm số đồng biến.
+ Sử dụng tính chất: Hàm số y= ax nghịch biến trên R khi 0< a< 1nên
Chọn C
Đúng 0
Bình luận (0)
Cho hàm số
y
f
x
. Đồ thị hàm số
y
f
x
như hình bên. Hỏi hàm số
g
x
f
3
−
x
2
đồng biến trong khoảng nào trong các khoảng sau? A. (-1;0) B. (0;1) C. (2;3) D. (-2;-1)
Đọc tiếp
Cho hàm số y = f x . Đồ thị hàm số y = f ' x như hình bên. Hỏi hàm số g x = f 3 − x 2 đồng biến trong khoảng nào trong các khoảng sau?
A. (-1;0)
B. (0;1)
C. (2;3)
D. (-2;-1)
Cho hàm số y f(x). Đồ thị hàm số
y
f
x
như hình bên. Hỏi hàm số
g
x
f
3
-
x
2
đồng biến trên khoảng nào trong các khoảng sau? A. (2;3) B. (-2;-1) C. (0;1) D. (-1;0)
Đọc tiếp
Cho hàm số y = f(x). Đồ thị hàm số y = f ' x như hình bên. Hỏi hàm số g x = f 3 - x 2 đồng biến trên khoảng nào trong các khoảng sau?
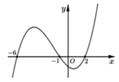
A. (2;3)
B. (-2;-1)
C. (0;1)
D. (-1;0)
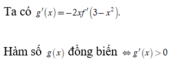
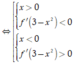
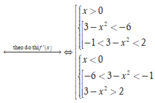
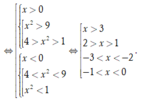
Chọn D.
Ta có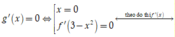 
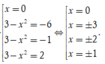
Bảng biến thiên
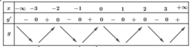
Dựa vào bảng biến thiên và đối chiếu với các đáp án, ta chọn D.
Đúng 0
Bình luận (0)
Cho hàm số y f( x) Đồ thị hàm số y f’( x) như hình bên. Hỏi hàm số y g(x) f( x2) đồng biến trên khoảng nào trong các khoảng sau? A. (
-
∞
;
-
1
) B. (-1;
+
∞
)
C. (-1; 0) D. (0;1)
Đọc tiếp
Cho hàm số y= f( x) Đồ thị hàm số y= f’( x) như hình bên. Hỏi hàm số y= g(x) = f( x2) đồng biến trên khoảng nào trong các khoảng sau?
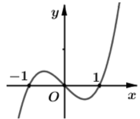
A. ( - ∞ ; - 1 )
B. (-1; + ∞ )
C. (-1; 0)
D. (0;1)
Cho hàm số yf(x) có đạo hàm
f
(
x
)
x
2
(
x
-
1
)
(
x
-
4
)
g
(
x
)
, trong đó
g
(
x
)
0
,
∀
x
. Hàm số
y
f
(
x
2...
Đọc tiếp
Cho hàm số y=f(x) có đạo hàm f ' ( x ) = x 2 ( x - 1 ) ( x - 4 ) g ( x ) , trong đó g ( x ) > 0 , ∀ x . Hàm số y = f ( x 2 ) đồng biến trên khoảng nào dưới đây?
A. ( - ∞ ; - 2 ) .
B. (-1;1).
C. (-2;-1).
D. (1;2).
Cho các hàm số y = 2 x 2 và y = -3x^2. Hỏi hàm số nào đồng biến khi x > 0
A. y = 2 x 2
B. y = -3 x 2
C. Không có hàm số nào
D. Cả hai
Đáp án A
Xét hàm số y = ax2 (a ≠ 0)
* Nếu a > 0 thì hàm số nghịch biến khi x < 0 và đồng biến khi x > 0.
* Nếu a < 0 thì hàm số đồng biến khi x < 0 và nghịch biến khi x > 0.
Do đó,chỉ có hàm số y = 2x2 đồng biến khi x> 0.
Đúng 0
Bình luận (0)
Cho hàm số y = f(x) có đạo hàm f'(x) = (x2-1)(x2-x-2). Hỏi hàm số g(x) = f(x-x2) đồng biến trên khoảng nào trong các khoảng sau?
A. (-1;1)
B. (0;2)
C. (-∞;-1)
D. (2;+∞)
\(f'\left(x\right)=\left(x-1\right)\left(x+1\right)\left(x+1\right)\left(x-2\right)=\left(x+1\right)^2\left(x-1\right)\left(x-2\right)\)
\(f'\left(x\right)=0\Rightarrow\left[{}\begin{matrix}x=1\\x=2\end{matrix}\right.\) (chỉ quan tâm nghiệm bội lẻ)
\(g'\left(x\right)=\left(1-2x\right)f'\left(x-x^2\right)=0\Rightarrow\left[{}\begin{matrix}x=\dfrac{1}{2}\\f'\left(x-x^2\right)=0\end{matrix}\right.\)
\(f'\left(x-x^2\right)=0\Rightarrow\left[{}\begin{matrix}x-x^2=1\\x-x^2=2\end{matrix}\right.\) (đều vô nghiệm)
\(\Rightarrow g\left(x\right)\) đồng biến khi \(x< \dfrac{1}{2}\) và nghịch biến khi \(x>\dfrac{1}{2}\)
\(\Rightarrow C\) đúng (do \(\left(-\infty;-1\right)\subset\left(-\infty;\dfrac{1}{2}\right)\)
Đúng 0
Bình luận (0)