Cho hai ví dụ về hàm số.
H24
Những câu hỏi liên quan
Cho hai ví dụ về hàm số bậc hai.
Ví dụ 1: \(y = 2{x^2} - x - 1\)
Ví dụ 2: \(y = - 3{x^2} + 1\)
Đúng 0
Bình luận (0)
Luyện tập – Vận dụng 1
Cho hai ví dụ về hàm số mũ
Luyện tập – Vận dụng 3
Cho hai ví dụ về hàm số lôgarit
\(log_3x;log_5\left(x+2\right)\)
Đúng 1
Bình luận (0)
Cho ví dụ về hàm số tuần hoàn.
Ví dụ về hàm số tuần hoàn là : \(g(x) = \left\{ \begin{array}{l}0\,\,\,\,\,\,\,,x \in Q\\1\,\,\,\,\,\,\,\,,x \in R\end{array} \right.\)
Đúng 0
Bình luận (0)
Cho 2 ví dụ về hàm số bậc nhất, trong đó 1 hàm số đồng biến, 1 hàm số nghịch biến
Hàm số đồng biến: y=x+10
Hàm số nghịch biến: y=-x+6
Đúng 2
Bình luận (0)
Nêu các bước vẽ đồ thị hàm số y = ax (a khác 0) (đã học ở lớp 7)
Đúng 0
Bình luận (1)
Cho ví dụ về hàm số bậc nhất trong các trường hợp sau:
Hàm số nghịch biến
Cho ví dụ về hàm số bậc nhất trong các trường hợp sau:
Hàm số đồng biến
Cho ví dụ về hàm số bậc nhất trong các trường hợp sau:
a) Hàm số đồng biến;
b) Hàm số nghịch biến.
a) Hàm số đồng biến là y = 2x + 5
b) Hàm số nghịch biến là y = -0,5x + 3
Các bài giải bài tập Toán 9 Tập 1 khác:
Đúng 0
Bình luận (0)
Vẽ đồ thị hàm số \(y = {x^2} - 4x + 3\) rồi so sánh đồ thị hàm số này với đồ thị hàm số trong Ví dụ 2z. Nếu nhận xét về hai đồ thị này.
Tham khảo:
Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai \(y = f(x) = {x^2} - 4x + 3\) là một parabol (P1):
+ Có đỉnh S với hoành độ: \({x_S} = \frac{{ - b}}{{2a}} = \frac{{ - ( - 4)}}{{2.1}} = 2;{y_S} = {2^2} - 4.2 + 3 = - 1.\)
+ Có trục đối xứng là đường thẳng \(x = 2\) (đường thẳng này đi qua đỉnh S và song song với trục Oy);
+ Bề lõm quay lên trên vì \(a = 1 > 0\)
+ Cắt trục tung tại điểm có tung độ bằng 3, tức là đồ thị đi qua điểm có tọa độ (0; 3).
Ta vẽ được đồ thị như hình dưới.
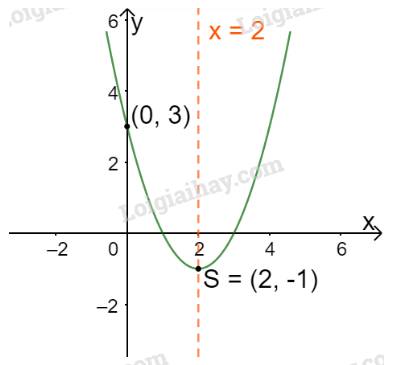
*So sánh với đồ thị hàm số ở Ví dụ 2a:
Giống nhau: Có chung trục đối xứng
Khác nhau:
Điểm đỉnh và giao điểm với trục tung của hai hàm số đối xứng với nhau qua trục Ox.
Bề lõm của (P) xuống dưới còn (P1) quay lên trên.
Nhận xét chung: Hai đồ thị này đối xứng với nhau qua trục Ox.
Đúng 0
Bình luận (0)
Cho em ví dụ thực tế về hàm số ( lớp 9 ) . Em cảm ơn ạ





