Vẽ hình biểu diễn của một hình vuông nội tiếp trong một hình tròn.
Vẽ hình biểu diễn của:
a) Một tam giác vuông nội tiếp trong một đường tròn;
b) Một lục giác đều.
Một đường tròn nội tiếp trong một hình vuông có cạnh bằng 5 . Sau đó nội tiếp trong hình vuông đó một hình tròn và quá trình đó cứ tiếp diễn như thế mãi. Nếu gọi Sn là tổng các diện tích của n hình tròn đầu tiên nội tiếp như thế. Tính S20.
Chân thành cảm ơn và hậu tạ.
Trong các hình vẽ ở hình vẽ, đường thẳng biểu diễn dòng điện không đổi I. Đường tròn trong mặt phẳng vuông góc với đường thẳng biểu diễn một đường sức của từ trường do dòng điện trong dây dẫn gây ra. Hình vẽ nào mô tả không đúng quan hệ giữa chiều dòng điện và chiều của đường sức từ?
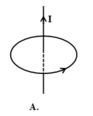
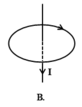
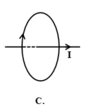
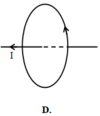
Đáp án: C
+ Đường sức từ do dòng điện thẳng gây ra có chiều được xác định theo qui tắc nắm tay phải: Để bàn tay phải sao cho ngón cái nằm dọc theo dây dẫn và chỉ theo chiều dòng điện, khi đó các ngón tay kia khum lại cho ta chiều của các đường sức từ.
Do vậy hình C mô tả không đúng quan hệ giữa chiều dòng điện và chiều của đường sức từ.
Trong các hình vẽ ở hình, đường thẳng biểu diễn dòng điện không đổi I. Đường tròn trong mặt phẳng vuông góc với đường thẳng biểu diễn một đường sức của từ trường do dòng điện trong dây dẫn gây ra. Hình vẽ nào mô tả không đúng quan hệ giữa chiều dòng điện và chiều của đường sức từ?
A. Hình A
B. Hình B
C. Hình C
D. Hình D
Đáp án C
+ Đường sức từ do dòng điện thẳng gây ra có chiều được xác định theo qui tắc nắm tay phải: Để bàn tay phải sao cho ngón cái nằm dọc theo dây dẫn và chỉ theo chiều dòng điện, khi đó các ngón tay kia khum lại cho ta chiều của các đường sức từ.
Do vậy hình C mô tả không đúng quan hệ giữa chiều dòng điện và chiều của đường sức từ.
Hãy vẽ hình biểu diễn của một đường tròn cùng với hai đường kính vuông góc của đường tròn đó.
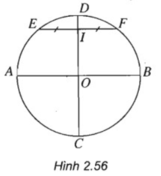
(h.2.56) Giả sử trên hình thực ta có đường tròn tâm O cùng với hai đường kính vuông góc của đường tròn đó là AB và CD. Nếu ta vẽ thêm một dây cung EF song song với AB thì đường kính CD sẽ đi qua trung điểm I của đoạn EF. Từ đó ta suy ra cách vẽ sau đây:
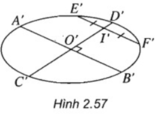
a) (h.2.57) Vẽ hình elip biểu diễn cho đường tròn và vẽ đường kính A'B' của hình elip đó. Đường kính này đi qua tâm O' của elip.
b) Vẽ một dây cung E'F' song song với đường kính A'B'. Gọi I' là trung điểm của E'F'. Đường thẳng O'I'cắt elip tại hai điểm C' và D'. Ta có A'B' và C'D' là hình biểu diễn của hai đường kính vuông góc với nhau của đường tròn.
Nhận xét. Hình bình hành A'C'B'D'là hình biểu diễn của hình vuông ACBD nội tiếp trong một đường tròn.
a) Vẽ hình vuông cạnh 4cm.
b) Vẽ đường tròn ngoại tiếp hình vuông đó. Tính bán kính R của đường tròn này.
c) Vẽ đường tròn nội tiếp hình vuông đó. Tính bán kính r của đường tròn này.
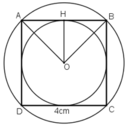
a) Vẽ hình vuông ABCD có cạnh 4cm.
b) Vẽ hai đường chéo AC và BD. Chúng cắt nhau tại O.
Đường tròn (O; OA) là đường tròn ngoại tiếp hình vuông ABCD.
Ta có:
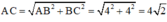 (cm)
(cm)
⇒ R = OA = AC/2 = 2√2 (cm).
c) Gọi H là trung điểm AB.
(O ; OH) là đường tròn nội tiếp hình vuông ABCD.
r = OH = AD/2 = 2cm.
Hãy vẽ hình biểu diễn của một đường tròn cùng với hai đường kính vuông góc của đường tròn đó ?
a) Vẽ đường tròn tâm O, bán kính 2cm.
b) Vẽ hình vuông nội tiếp đường tròn (O) ở câu a).
c) Tính bán kính r của đường tròn nội tiếp hình vuông ở câu b) rồi vẽ đường tròn (O; r).
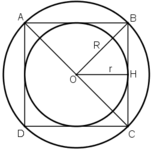
a) Chọn điểm O là tâm, mở compa có độ dài 2cm vẽ đường tròn tâm O, bán kính 2cm.
b) Vẽ đường kính AC và BD vuông góc với nhau. Nối A với B, B với C, C với D, D với A ta được tứ giác ABCD là hình vuông nội tiếp đường tròn (O; 2cm).
c) Vẽ OH ⊥ BC.
⇒ OH là khoảng cách từ từ tâm O đến BC
Vì AB = BC = CD = DA ( ABCD là hình vuông) nên khoảng cách từ tâm O đến AB, BC, CD, DA bằng nhau ( định lý lien hệ giữa dây cung và khoảng cách từ tâm đến dây)
⇒ O là tâm đường tròn nội tiếp hình vuông ABCD
OH là bán kính r của đường tròn nội tiếp hình vuông ABCD.
Tam giác vuông OBC có OH là đường trung tuyến ⇒ 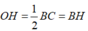
Xét tam giác vuông OHB có: r 2 + r 2 = O B 2 = 2 2 ⇒ 2 r 2 = 4 ⇒ r 2 = 2 ⇒ r = 2 ( cm )
Vẽ đường tròn (O; OH). Đường tròn này nội tiếp hình vuông, tiếp xúc bốn cạnh hình vuông tại các trung điểm của mỗi cạnh.
Kiến thức áp dụng
+ Đường tròn ngoại tiếp đa giác nếu đường tròn đó đi qua tất cả các đỉnh của đa giác. Khi đó ta nói đa giác nội tiếp đường tròn.
+ Đường tròn nội tiếp đa giác là đường tròn tiếp xúc với tất cả các cạnh của đa giác. Khi đó ta nói đa giác ngoại tiếp đường tròn.