Hãy chỉ ra một số thực T sao cho sin(x + T) = sinx với mọi \(x \in \mathbb{R}\).
H24
Những câu hỏi liên quan
Xét tập hợp \(D = \mathbb{R}\backslash \left\{ {\frac{\pi }{2} + k\pi |\,k \in \mathbb{Z}} \right\}\). Với mỗi số thực \(x \in D\), hãy nêu định nghĩa \(\tan x\)
\(\tan x = \frac{{\sin x}}{{\cos x}}\)
Đúng 0
Bình luận (0)
a) Lấy ba ví dụ về tập hợp và chỉ ra một số phần tử của chúng.
b) Với mỗi tập hợp \(\mathbb{N},\mathbb{Z},\mathbb{Q},\mathbb{R}\), hãy sử dụng kí hiệu \( \in \) và \( \notin \)để chỉ ra hai phần tử thuộc hai phần tử không thuộc tập hợp đó.
a) A là tập hợp các số tự nhiên nhỏ hơn 5, khi đó \(0 \in A,2 \in A,3 \in A.\)
B là tập hợp các nghiệm thực của phương trình \({x^2} - 3x + 2 = 0\), khi đó \(1 \in B,2 \in B.\)
C là tập hợp các thứ trong tuần, khi đó chủ nhật \( \in C,\) thứ năm \( \in C.\)
b)
\(\begin{array}{l}0 \in \mathbb{N},\;2 \in \mathbb{N}, - 5 \notin \mathbb{N},\;\frac{2}{3} \notin \mathbb{N}.\\0 \in \mathbb{Z},\; - 5 \in \mathbb{Z},\frac{2}{3} \notin \mathbb{Z},\sqrt 2 \; \notin \mathbb{Z}.\\0 \in \mathbb{Q},\;\frac{2}{3} \in \mathbb{Q},\sqrt 2 \notin \mathbb{Q},\;\pi \notin \mathbb{Q}.\\\frac{2}{3} \in \mathbb{R},\;\sqrt 2 \in \mathbb{R},e \notin \mathbb{R},\;\pi \notin \mathbb{R}.\end{array}\)
Đúng 0
Bình luận (0)
tìm m để hàm số sau xác định\(\forall x\in\mathbb{R}\) :
y=\(\sqrt{sin^4x+cos^4x-2m\sin x\cos x}\)
Để hàm số xác định \(\forall x\in R\Leftrightarrow sin^4x+cos^4x-2msinx.cosx\ge0\) \(\forall x\)
Ta có:
\(sin^4x+cos^4x-2msinx.cosx=\left(sin^2x+cos^2x\right)^2-2\left(sinx.cosx\right)^2-m.sin2x\)
\(=1-2\left(\frac{1}{2}sin2x\right)^2-msin2x=-\frac{1}{2}sin^22x-msin2x+1\)
Xét \(f\left(t\right)=-\frac{1}{2}t^2-mt+1\) với \(t\in\left[-1;1\right]\)
\(f\left(-1\right)=\frac{1}{2}+m\) ; \(f\left(1\right)=\frac{1}{2}-m\)
Để \(f\left(t\right)\ge0\) \(\forall t\in\left[-1;1\right]\Rightarrow\min\limits_{\left[-1;1\right]}f\left(t\right)\ge0\)
\(\Rightarrow\left\{{}\begin{matrix}f\left(-1\right)\ge0\\f\left(1\right)\ge0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}m\ge-\frac{1}{2}\\m\le\frac{1}{2}\end{matrix}\right.\) \(\Rightarrow-\frac{1}{2}\le m\le\frac{1}{2}\)
Đúng 0
Bình luận (1)
Xét tập hợp \(E = R\backslash \left\{ {k\pi |k \in \mathbb{Z}} \right\}\). Với mỗi số thực \(x \in E\), hãy nêu định nghĩ \(\cot x\)
\(\cot x = \frac{{\cos x}}{{\sin x}}\)
Đúng 0
Bình luận (0)
\(\cot x=\dfrac{\cos x}{\sin x}\)
Đúng 0
Bình luận (0)
Tập xác định của hàm số y frac{{cos x}}{{sin x - 1}} làA. mathbb{R}backslash { k2pi {rm{|}}k; in ;mathbb{Z}{rm{} }} B. mathbb{R};backslash left{ {frac{pi }{2} + k2pi {rm{|}}k; in ;mathbb{Z}} right}C. mathbb{R}backslash left{ {frac{pi }{2} + kpi {rm{|}}k; in ;mathbb{Z}} right} D. mathbb{R}backslash { kpi {rm{|}}k; in ;mathbb{Z}{rm{} }}
Đọc tiếp
Tập xác định của hàm số \(y = \frac{{\cos x}}{{\sin x - 1}}\) là
A. \(\mathbb{R}\backslash \{ k2\pi {\rm{|}}k\; \in \;\mathbb{Z}{\rm{\} }}\)
B. \(\mathbb{R}\;\backslash \left\{ {\frac{\pi }{2} + k2\pi {\rm{|}}k\; \in \;\mathbb{Z}} \right\}\)
C. \(\mathbb{R}\backslash \left\{ {\frac{\pi }{2} + k\pi {\rm{|}}k\; \in \;\mathbb{Z}} \right\}\)
D. \(\mathbb{R}\backslash \{ k\pi {\rm{|}}k\; \in \;\mathbb{Z}{\rm{\} }}\)
Hàm số xác định khi: \(\sin x - 1\; \ne 0\; \Leftrightarrow \sin x \ne 1\; \Leftrightarrow x \ne \frac{\pi }{2} + k2\pi ,\;\;k \in \mathbb{Z}\)
Vậy ta chọn đáp án B
Đúng 0
Bình luận (0)
Tìm giá trị của m để:
a) \(2{x^2} + 3x + m + 1 > 0\) với mọi \(x \in \mathbb{R}\);
b) \(m{x^2} + 5x - 3 \le 0\) với mọi \(x \in \mathbb{R}\)
a) Tam thức \(2{x^2} + 3x + m + 1\) có \(\Delta = {3^2} - 4.2.\left( {m + 1} \right) = 1 - 8m\)
Vì \(a = 2 > 0\) nên để \(2{x^2} + 3x + m + 1 > 0\) với mọi \(x \in \mathbb{R}\) khi và chỉ khi \(\Delta < 0 \Leftrightarrow 1 - 8m < 0 \Leftrightarrow m > \frac{1}{8}\)
Vậy khi \(m > \frac{1}{8}\) thì \(2{x^2} + 3x + m + 1 > 0\) với mọi \(x \in \mathbb{R}\)
b) Tam thức \(m{x^2} + 5x - 3\) có \(\Delta = {5^2} - 4.m.\left( { - 3} \right) = 25 + 12m\)
Đề \(m{x^2} + 5x - 3 \le 0\) với mọi \(x \in \mathbb{R}\) khi và chỉ khi \(m < 0\) và \(\Delta = 25 + 12m \le 0 \Leftrightarrow m \le - \frac{{25}}{{12}}\)
Vậy \(m{x^2} + 5x - 3 \le 0\) với mọi \(x \in \mathbb{R}\) khi \(m \le - \frac{{25}}{{12}}\)
Đúng 0
Bình luận (0)
Nhập số tự nhiên n và số thực x. Tính
A=sinx+sin2x+...+sinnx
B=sinx+sinx2+...+sinxn
var i,n:integer;
x,y,A:real;
begin
write('Nhap gia tri cho x va n');
readln(x,n);
A:=0;
y:=1;
for i:=1 to n do
begin
y:=y*sin(x);
A:= A + y;
end;
write('Tong A la: ',A:8:4);
readln
end.
Cho hàm số fleft( x right) x + 1 với x in mathbb{R}.a) Giả sử {x_0} in mathbb{R}. Hàm số fleft( x right) có liên tục tại điểm {x_0} hay không?b) Quan sát đồ thị hàm số fleft( x right) x + 1 với x in mathbb{R} (Hình 13), nếu nhận xét về đặc điểm của đồ thị hàm số đó.
Đọc tiếp
Cho hàm số \(f\left( x \right) = x + 1\) với \(x \in \mathbb{R}.\)
a) Giả sử \({x_0} \in \mathbb{R}.\) Hàm số \(f\left( x \right)\) có liên tục tại điểm \({x_0}\) hay không?
b) Quan sát đồ thị hàm số \(f\left( x \right) = x + 1\) với \(x \in \mathbb{R}\) (Hình 13), nếu nhận xét về đặc điểm của đồ thị hàm số đó.
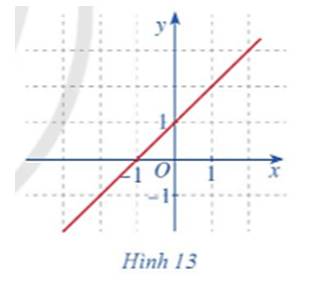
a) Ta có \(f\left( {{x_0}} \right) = {x_0} + 1;\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = \mathop {\lim }\limits_{x \to {x_0}} \left( {x + 1} \right) = \mathop {\lim }\limits_{x \to {x_0}} x + 1 = {x_0} + 1\)
\( \Rightarrow \mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = f\left( {{x_0}} \right)\)
Vậy hàm số \(f\left( x \right)\) liên tục tại \({x_0}.\)
b) Dựa vào đồ thị hàm số ta thấy: Đồ thị hàm số là một đường thẳng liền mạch với mọi giá trị \(x \in \mathbb{R}.\)
Đúng 0
Bình luận (0)
Rút gọn các biểu thức sau
a) A= sin^2 30° +sin^2 240° +sin^2 50° +sin^2 60°
b) Cho cotg x=2 .Tính gtri biểu thức = sinx + cosx : sinx - cosx
Mình cần gấp giúp mình với :(((
\(A=sin^230+sin^260+sin^240+sin^250\)
\(=sin^230+cos^2\left(90-60\right)+sin^240+cos^2\left(90-50\right)\)
\(=sin^230+cos^230+sin^240+cos^240\)
\(=1+1=2\)
\(B=\frac{sinx+cosx}{sinx-cosx}=\frac{\frac{sinx}{sinx}+\frac{cosx}{sinx}}{\frac{sinx}{sinx}-\frac{cosx}{sinx}}=\frac{1+cotx}{1-cotx}=\frac{1+2}{1-2}=-3\)


