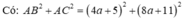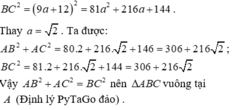Tam giác ABC có AB/5 BC/12=AC/13 có phải tam giác vuông không
TT
Những câu hỏi liên quan
Tam giác ABC có phải là tam giác vuông không biết AB = 4a + 5, BC= 9a + 12, AC = 8a + 11, với a là độ dài cạnh huyền của tam giác vuông cân có độ dài cạnh góc vuông là 1
Cho tam giác ABC, có AB= 12 cm, BC= 13 cm, AC= 5 cm. Chứng minh tam giác ABC vuông
ta có AB2+AC2=122+52=144+25=169
BC2=132=169
==> AB2+AC2=BC2
==> Tam giác ABC vuông
Đúng 0
Bình luận (0)
Cho tam giác ABC từ A Kẻ AH vuông góc với BC (H nằm giữa B và C) biết AC = 12 cm ah = 60/13 cm BH = 25/13 cm
a) tính AB;BC
b) tam giác ABC có phải là tam giác vuông không? Vì sao?
c)Kẻ HM vuông góc với AC tại M. Tính độ dài HM
Tam giác ABC có phải là tam giác vuông không nếu các cạnh AB, AC, BC tỉ lệ với 9, 12 và 15
\(TC:\)
\(BC^2=15^2=225\)
\(AB^2+AC^2=9^2+12^2=255\)
\(\Rightarrow BC^2=AB^2+AC^2\)
\(\Rightarrow\Delta ABC\perp A\)
Đúng 0
Bình luận (0)
Vì AB,AC,BC tỉ lệ với 9;12;15 nên \(\dfrac{AB}{9}=\dfrac{AC}{12}=\dfrac{BC}{15}\)
Đặt \(\dfrac{AB}{9}=\dfrac{AC}{12}=\dfrac{BC}{15}=k\)
nên \(\left\{{}\begin{matrix}AB=9k\\AC=12k\\BC=15k\end{matrix}\right.\)
Vì \(\left(15k\right)^2=\left(9k\right)^2+\left(12k\right)^2\)
nên \(BC^2=AB^2+AC^2\)
Xét ΔABC có \(BC^2=AB^2+AC^2\)(cmt)
nên ΔABC vuông tại A(Định lí Pytago đảo)
Đúng 0
Bình luận (1)
Tam giác ABC có phải là tam giác vuông hay không nếu các cạnh AB; AC; BC tỉ lệ với
9; 12 và 15
Ta có các cạnh AB; AC; BC tỉ lệ với 9; 12 và 15
⇒ \(\dfrac{AB}{9}=\dfrac{AC}{12}=\dfrac{BC}{15}\)
Đặt \(\dfrac{AB}{9}=\dfrac{AC}{12}=\dfrac{BC}{15}=k\)
⇒ \(\left\{{}\begin{matrix}AB=9k\\AC=12k\\BC=15k\end{matrix}\right.\)
Ta có:
\(AB^2+AC^2=BC^2\)
\(\left(9k\right)^2+\left(12k\right)^2=\left(15k\right)^2\)
\(81k^2+144k^2=225k^2\)
\(225k^2=225k^2\)
Áp dụng định lý Pytago đảo
⇒ Tam giác ABC vuông tại A
Đúng 2
Bình luận (0)
Xét tam giác ABC,BC=15
BC²=15²=225
Tổng bình phương hai cạnh góc vuông:
AB²+AC²=9²+12²=81+144=255
=>BC²=AB²+AC²
Vậy tam giác ABC là tam giác vuông
Đúng 1
Bình luận (0)
-Theo đề bài ta có:
\(\dfrac{AB}{9}=\dfrac{AC}{12}=\dfrac{BC}{15}\)
\(\Rightarrow AB=\dfrac{3}{5}BC;AC=\dfrac{4}{5}BC\)
\(\Rightarrow AB^2=\dfrac{9}{25}BC^2;AC^2=\dfrac{16}{25}BC^2\)
\(\Rightarrow AB^2+AC^2=\dfrac{9}{25}BC^2+\dfrac{16}{25}BC^2=\left(\dfrac{9}{25}+\dfrac{16}{25}\right)BC^2=\dfrac{25}{25}BC^2=BC^2\)-Xét △ABC có:
\(AB^2+AC^2=BC^2\) (cmt)
\(\Rightarrow\)△ABC vuông tại A (định lí Py-ta-go đảo).
Đúng 0
Bình luận (0)
Tam giác ABC có AB=6cm AC=8cm BC=10cm. Tam giác ABC có phải là tam giác vuông không?
Xét ΔABC có \(AB^2+AC^2=BC^2\)
nên ΔABC vuông tại A
Đúng 0
Bình luận (0)
7.: Tam giác ABC có phải là tam giác vuông hay không nếu các cạnh AB; AC; BC tỉ lệ với 9; 12 và 15
Đặt AB/9=AC/12=BC/15=k
=>AB=9k; AC=12k; BC=15k
Xét ΔABC có \(BC^2=AB^2+AC^2\)
nên ΔABC vuông tại A
Đúng 1
Bình luận (0)
Tam giác ABC có phải là tam giác vuông hay không nếu các cạnh AB; AC; BC tỉ lệ với 9: 12 và 15
Là tam giác vuông đó bạn
Vì 152=92+122
Đúng 0
Bình luận (0)
cho hình tam giác ABC vuông ở A có chu vi 30 cm , biết cạnh góc vuông AB = 5/12 cạnh góc vuông AC ,cạnh BC = 13 cm .Tính diện tích tam giác vuông ABC?
Tổng độ dài hai cạnh AB và AC:
30 - 13 = 17 (cm)
Tổng số phần bằng nhau:
5 + 12 = 17 (phần)
Cạnh AB dài:
17 . 5 : 17 = 5 (cm)
Cạnh AC dài:
17 . 12 : 17 = 12 (cm)
Diện tích tam giác ABC:
5 . 12 : 2 = 30 (cm²)
Đúng 3
Bình luận (0)
Tổng độ dài 2 đáy AB và AC là :
30 - 13 = 17 ( cm )
Tổng số phần bằng nhau là
5 + 12 = 17 ( phần )
Cạnh AB dài là
17 : 17 x 5 = 5 ( cm )
Cạnh AC dài là :
17 - 5 = 12 ( cm )
Diện tích hình tam giác vuông ABC là
12 x 5 : 2 = 30 ( m2)
Đáp số : 30 m2
Đúng 2
Bình luận (1)