Vẽ hình và chứng minh tính chất đường phân giác trong và ngoài của tam giác.
HN
Những câu hỏi liên quan
Chứng minh rằng trong một tam giác hai đường phân giác 2 góc ngoài của tam giác và đường phân giác trong của đỉnh còn lại đồng quy.
(vẽ hình và ghi lời giải đầy đủ, ban nào làm xong sớm và đúng mình sẽ tick)
cho tam giác ABC hai tia phân giác của góc trong B và C cắt nhau tại M.Hai tia phân giác của góc ngoài B và C cắt nhau tại N Chứng minh rằng tứ giác BMCN nối tiếp đường tròn.(giải chi tiết và vẽ hình)
BM,BN là phân giác của hai góc kề bù
=>góc MBN=90 độ
CM,CN là phân giác của haigóc kề bù
=>góc MCN=90 độ
Vì góc MBN+góc MCN=180 độ
nên MBNC nội tiếp
Đúng 0
Bình luận (0)
Cho tam giác ABC, gọi P,Q là hình chiếu của điểm A trên đường phân giác trong và ngoài của góc B.Gọi M, N là hình chiếu của điểm A trên đường phân giác trong và ngoài của góc C
a) Tứ giác AQBP và AMCN là hình gì
b) Chứng minh Q, M, P, N thẳng hàng
Em cần hình vẽ ạ
Giúp em với :(
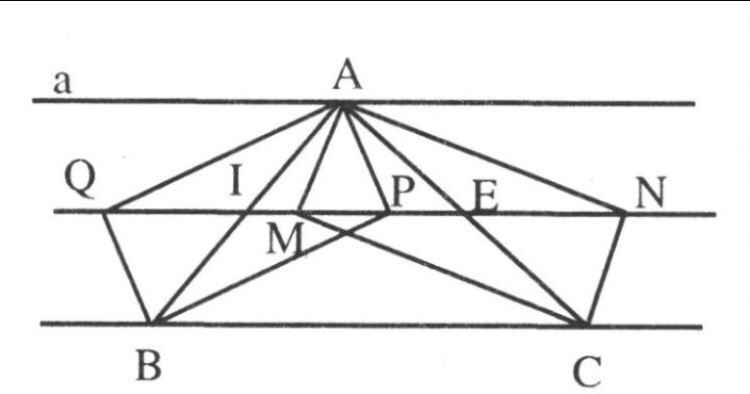
a. Vì BQ và BP là p/g ngoài và trong của \(\widehat{ABC}\) nên \(BP\bot BQ\)
Lại có \(AQ\bot BQ, AP\bot BP\) nên AQPB là hcn
Cmtt ta được AMCN cũng là hcn
b. Gọi I là giao 2 đường chéo AB và PQ của hcn AQBP
\(\Rightarrow IB=IA=IC\\ \Rightarrow\widehat{IPB}=\widehat{IBP}=\widehat{PBC}\left(BP\text{ là p/g}\right)\)
Mà 2 góc này ở vị trí slt nên IP//BC
\(\Rightarrow P,Q\) nằm trên đtb của \(\Delta ABC\)
Tương tự M,N cũng nằm trên đtb \(\Delta ABC\)
Vậy M,N,Q,P thẳng hàng
Đúng 1
Bình luận (1)
Cho tam giác ABC. Gọi M, N lần lượt là hình chiếu của điểm A trên đường phân giác trong và ngoài của góc B; E, F lần lượt là hình chiếu của điểm A trên đường phân giác trong và ngoài của góc C.
a) Chứng minh bốn điểm M, N, E, F thẳng hàng.
b) Tính độ dài cạnh NF theo các cạnh của tam giác ABC.
Cho tam giác ABC có AB=2cm AC=3cm BC=10cm Vẽ Ax là tia dối của tia AC. Vẽ AD và AE lần lượt là đường phân giác trong và đường phân giác ngoài 1. Chứng minh góc DAB + EAB=90• và tam giác ADE vuông tại A. 2. AM là đường trung tuyến của tam giác ADE. Tính BD và EB. 3. Tính DE và AM
Chứng minh tính chất đường phân giác ngoài trong tam giác
Tham khảo:
Đường phân giác ngoài tại một đỉnh của một tam giác là đường thẳng chia cạnh đối diện thàng hai đoạn thẳng tỉ lệ với hai cạnh kề với hai đoạn thẳng ấy. Ví dụ: Trong tam giác ABC, có AD là phân giác ngoài của góc A và AD cắt BC tại D. Như vậy, ta có: DB/DC = AB/AC.
HT
TL:
Tham khảo: Đường phân giác ngoài tại một đỉnh của một tam giác là đường thẳng chia cạnh đối diện thàng hai đoạn thẳng tỉ lệ với hai cạnh kề với hai đoạn thẳng ấy. Ví dụ: Trong tam giác ABC, có AD là phân giác ngoài của góc A và AD cắt BC tại D. Như vậy, ta có: DB/DC = AB/AC.
k cho mik nhé
@@@@@@@@@@@@@@@@@@@@@@@
HT
TL:
Tham khảo: Đường phân giác ngoài tại một đỉnh của một tam giác là đường thẳng chia cạnh đối diện thàng hai đoạn thẳng tỉ lệ với hai cạnh kề với hai đoạn thẳng ấy. Ví dụ: Trong tam giác ABC, có AD là phân giác ngoài của góc A và AD cắt BC tại D. Như vậy, ta có: DB/DC = AB/AC.
k nhé
@@@@@@@@@@@@@@@@@@@@@@@@@@@@
HT
Cho tam giác ABC không cân, vẽ phân giác trong Ax. Vẽ đường thẳng d là trung trực của BC. Gọi E là giao điểm của Ax và d. Chứng minh E nằm ngoài tam giác ABC.
Cho tam giác ABC có AB=2cm AC=3cm BC=10cm Vẽ Ax là tia dối của tia AC. Vẽ AD và AE lần lượt là đường phân giác trong và đường phân giác ngoài
1. Chứng minh góc DAB + EAB=90• và tam giác ADE vuông tại A.
2. AM là đường trung tuyến của tam giác ADE. Tính BD và EB.
3. Tính DE và AM
Cho tam giác ABC có các đường phân giác trong là BE và CF cắt nhau tại M và các đường phân giác ngoài của các góc B và góc C cắt nhau tại N. Chứng minh tứ giác BMNC là tứ giác nội tiếp
Vẽ hình ra luôn
GIÚP MÌNH NHA MAI MÌNH NỘP RỒI!!!!!!
Tự Vẽ Hình Nhé :
Theo tính chất đường phân giác ngoài của một góc luôn vuông góc với đường phân giác ngoài của góc đó
=> \(\widehat{MBN}=\widehat{MCN}=90^0\)nên hai góc \(\widehat{MBN}\)và \(\widehat{MCN}\)cùng nhìn MN dưới một góc bằng 90 độ. vậy Tứ giác MBNC nội tiếp đường tròn đường kính MN
Đúng 0
Bình luận (0)
mk ko có bít làm sao jờ ?
?????????????????
Cho tam giác ABC có các đường phân giác trong là BE và CF cắt nhau tại M và các đường phân giác ngoài của các góc B và góc C cắt nhau tại N. Chứng minh tứ giác BMNC là tứ giác nội tiếp
Vẽ hình ra luôn
mk ko bít????tự làm nhé ^_^ !
Đúng 0
Bình luận (0)




