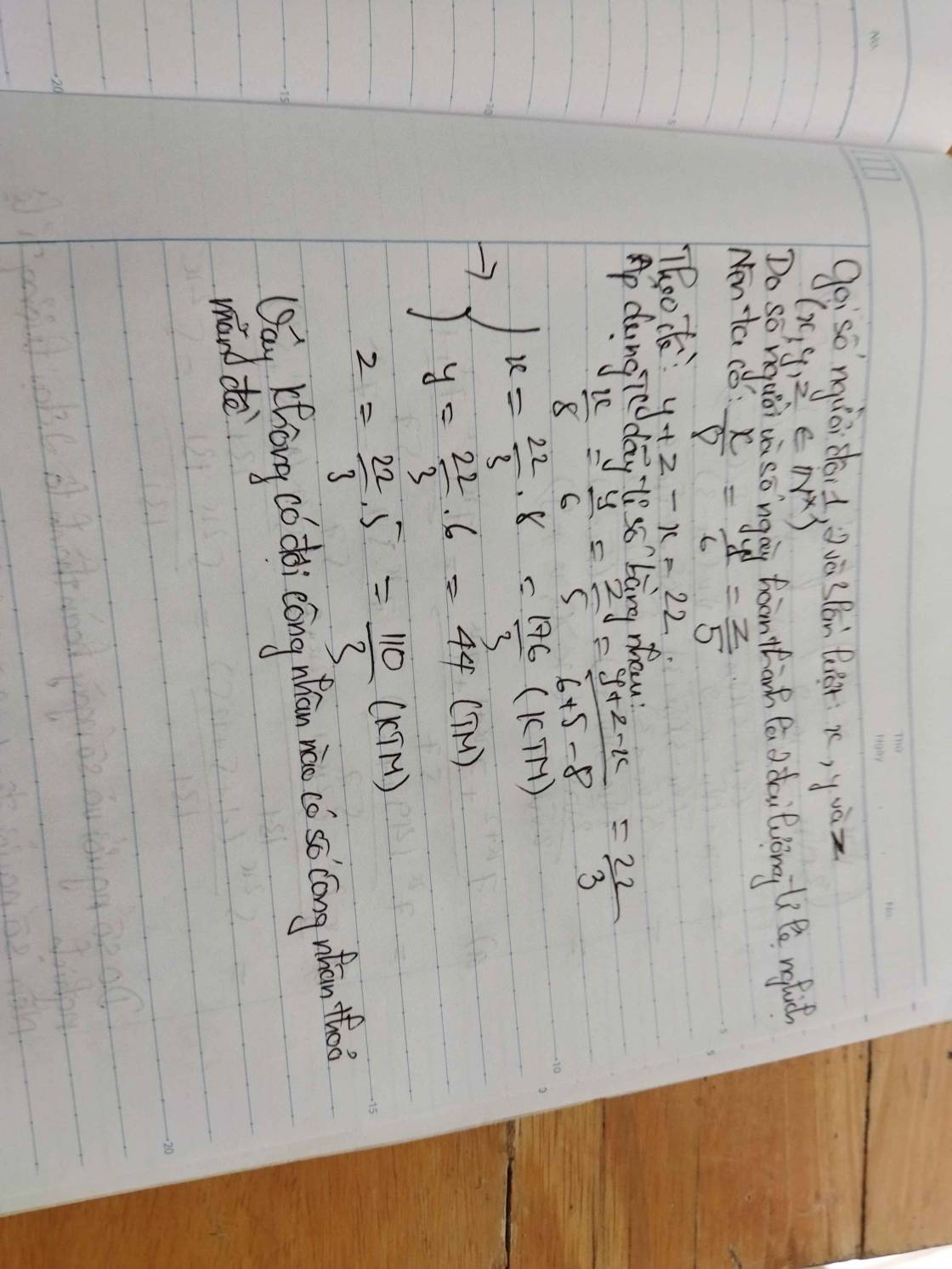Gọi x,y,z là số tiền thưởng của ba công nhân lần lượt  (15>x,y,z > 0)

Vì năng suất lao động tương ứng tỉ lệ với 2;4;6 nên số tiền thưởng cũng tỉ lệ thuận với 2;4;6 

Ta có:  x 2 = y 4 = z 6  và  x + y + z = 15

Áp dụng tính chất của dãy tỉ số bằng nhau ta có:

x 2 = y 4 = z 6 = x + y + z 2 + 4 + 6 = 15 12 = 1 , 25

Suy ra: x = 1,25.2 = 2,5 (triệu đồng)

Số tiền người A được thưởng là 2,5 triệu đồng

Đáp án cần chọn là C

Gọi x,y,z là số tiền thưởng của ba công nhân lần lượt  (x,y,z > 0)

Gỉa sử x,y,z tỉ lệ thuận với 3;4;7  ta có:  x 3 = y 5 = z 7  và x+ y = 5,6

Áp dụng tính chất của dãy tỉ số bằng nhau ta có:

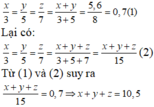
Tổng số tiền thưởng của ba người là 10,5 triệu

Đáp án cần chọn là C

 Gọi tiền thưởng của 3 người lần lượt là a,b,c (triệu)(a,b,c>0).
Tổng số tiền thưởng của ng1 và ng2 là 5,6 triệu đồng nên a+b=5,6
Số tiền thưởng tỉ lệ thuận với năng suất lao động nên: a3=b5=c7=a+b3+5=5,68=0,7.
⇒a=0,7.3=2,1(tr);b=0,7.5=3,5(tr);c=0,7.7=4,9(tr).
Do đó tổng tiền thưởng của 3ng là:2,1+3,5+4,9=10,5(tr).

Nếu đúng thì tích mình nha bạn 

mk thử 10.5 tr rồi mà k đúng bạn ak

Giải:

Gọi số tiền thưởng của 3 người lần lượt là a, b, c ( a,b,c thuộc N* )

Ta có:

\(\frac{a}{3}=\frac{b}{5}=\frac{c}{7}\) và \(a+b=5600000\)

Áp dụng tính chất của dãy tỉ số bằng nhau ta có:

\(\frac{a}{3}=\frac{b}{5}=\frac{c}{7}=\frac{a+b}{3+5}=\frac{5600000}{8}=700000\)

+) \(\frac{a}{3}=700000\Rightarrow a=2100000\)

+) \(\frac{b}{5}=700000\Rightarrow b=3500000\)

+) \(\frac{c}{7}=700000\Rightarrow c=4900000\)

Vậy người thứ nhất được 2100000 đồng ( 2.1 triệu )

        người thứ 2 được 3500000 đồng ( 3.5 triệu )

        người thứ 3 được 4900000 đồng ( 4.9 triệu )

Gọi tiền thưởng của 3 người lần lượt là a,b,c (triệu)(a,b,c>0).

Tổng số tiền thưởng của người 1 và người 2 là 5,6 triệu đồng nên a+b=5,6
Số tiền thưởng tỉ lệ thuận với năng suất lao động nên: 

\(\frac{a}{3}=\frac{b}{5}=\frac{c}{7}=\frac{a+b}{3+5}=\frac{5,6}{8}=0,7\)

\(\Rightarrow a=0,7.3=2,1\) ;\(b=0,7.5=3.5\) ;\(c=0,7.7\) =4,9

Do đó tổng tiền thưởng của 3ng là:$2,1+3,5+4,9=10,5\left(tr\right)$.

Gọi số tiền của 3 người thợ lần lượt là x,y,z

Vì số tiền thưởng và năng suất lao động là 2 đại lượng tỉ lệ thuận nên

\(\dfrac{x}{3}=\dfrac{y}{5}=\dfrac{z}{7}\)

Theo tính chất của dãy tỉ số bằng nhau, ta có:

\(\dfrac{z}{7}=\dfrac{x}{3}=\dfrac{y}{5}=\dfrac{z-x}{7-3}=\dfrac{200000}{4}=50000\)

\(\Rightarrow x=50000.3=150000\)

\(y=50000.5=250000\)

\(z=50000.7=350000\)

Số tiền thưởng của 3 người thợ lần lượt là 150000,250000,350000 ( đồng )

a) Gọi số tiền thưởng của ba người lần lượt là a,b,c(triệu đồng)

Theo điều kiện của bài ta có : \(a:b:c=3:5:7\)hoặc \(\frac{a}{3}=\frac{b}{5}=\frac{c}{7}\)và a + b = 5,6

Áp dụng tính chất dãy tỉ số bằng nhau ta có :

\(\frac{a}{3}=\frac{b}{5}=\frac{c}{7}=\frac{a+b}{3+5}=\frac{5,6}{8}=0,7\)

=> \(\hept{\begin{cases}\frac{a}{3}=0,7\\\frac{b}{5}=0,7\\\frac{c}{7}=0,7\end{cases}}\Rightarrow\hept{\begin{cases}a=2,1\\b=3,5\\c=4,9\end{cases}}\)

=> \(a+b+c=2,1+3,5+4,9=10,5\)

Vậy tổng số tiền của ba người được thưởng là 10,5 triệu đồng

Còn câu b bạn tự làm đi nhé