

Giải chi tiết cho mình bài này vớiii

Giải chi tiết cho mình 2 bài này vớiii
I
1. c
2. d
3. b
4. d
5. d
II
1. a (trọng âm rơi 2 còn lại rơi âm 3)
2. b (trọng âm rơi 2 còn lại rơi âm 1)
3. c (trọng âm rơi 2 còn lại rơi âm 1)
4. d (trọng âm rơi 3 còn lại rơi âm 2)
5. a (trọng âm rơi 2 còn lại rơi âm 1)
IX
1. a
2. a
3. c
4. a
5. a
Bài I, II tớ làm bên dưới roi. Có gi k thắc mắc ib tớ nha.
Giải chi tiết cho mình bài này nhé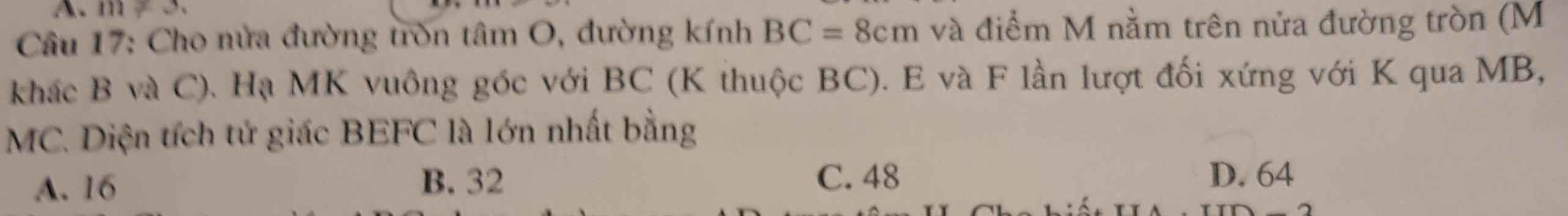
\(\widehat{BME}=\widehat{BMK}\) (do K đối xứng E qua MB)
Mà \(\widehat{BMK}=\widehat{BCM}\) (cùng phụ \(\widehat{MBC}\))
\(\Rightarrow\widehat{BME}=\widehat{BCM}\)
\(\Rightarrow ME\) là tiếp tuyến của (O) tại M
Tương tự, ta có MF là tiếp tuyến của (O) tại M
\(\Rightarrow M;E;F\) thẳng hàng
\(\Rightarrow S_{BEFC}=S_{BEMK}+S_{CFMK}=2S_{BMK}+2S_{CMK}=2S_{MBC}\)
Mà \(S_{MBC}=\dfrac{1}{2}MK.BC\Rightarrow S_{MBC-max}\) khi \(MK_{max}\)
\(\Rightarrow M\) nằm chính giữa cung BC \(\Rightarrow MK_{max}=R=4\left(cm\right)\)
\(\Rightarrow S_{BEFC-max}=2.\dfrac{1}{2}.4.8=32\left(cm^2\right)\)
giải chi tiết cho mình bài này nhé
để A là số nguyên thì \(x-9-5⋮\sqrt{x}+3\)
\(\Leftrightarrow\sqrt{x}+3\inƯ\left(5\right)\)
\(\Leftrightarrow\sqrt{x}+3=5\)
hay x=4
giải chi tiết cho mình bài này nhé
TH1: \(x=14\Rightarrow A=0\) (thỏa mãn)
TH2: \(x\ne14\Rightarrow A\) nguyên khi \(x\) là SCP và \(\dfrac{x-14}{\sqrt{x}+3}\in Z\Rightarrow\dfrac{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)-5}{\sqrt{x}+3}\in Z\)
\(\Rightarrow\sqrt{x}-3-\dfrac{5}{\sqrt{x}+3}\in Z\)
\(\Rightarrow\dfrac{5}{\sqrt{x}+3}\in Z\Rightarrow\sqrt{x}+3=Ư\left(5\right)=5\) (do \(\sqrt{x}+3\ge3\))
\(\Rightarrow x=4\)
Vậy \(x=\left\{4;14\right\}\) có 2 giá trị
giải chi tiết cho mình bài này nhé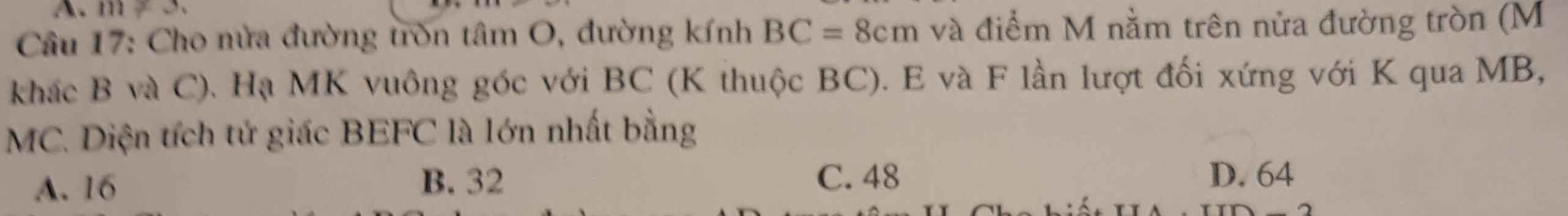
giải chi tiết cho mình bài này với ạ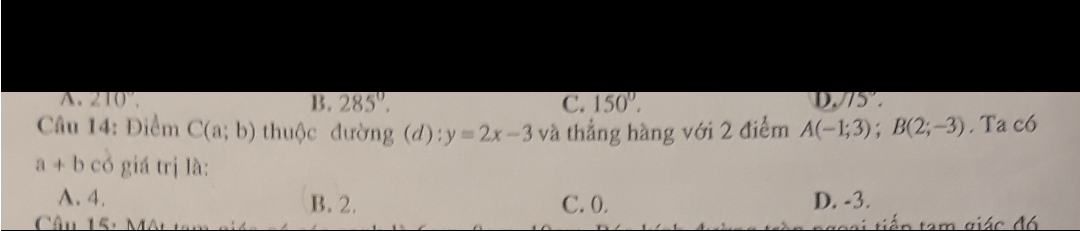
Gọi phương trình đường thẳng đi qua 2 điểm \(A,B\) là \(y=mx+n\)
Do \(\left\{{}\begin{matrix}A\in AB\\B\in AB\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}3=-m+n\\-3=2m+n\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}m=-2\\n=1\end{matrix}\right.\)
\(\Rightarrow AB:y=-2x+1\)
Do \(C\left(a,b\right)\in\left(d\right):y=2x-3\Rightarrow b=2a-3\) (1)
Mặt khác, để \(A,B,C\) thẳng hàng thì \(C\in AB\Rightarrow b=-2a+1\) (2)
Từ (1) và (2) ta có \(a=1,b=-1\) nên \(a+b=0\)
Do C thuộc d nên: \(b=2a-3\) \(\Rightarrow C\left(a;2a-3\right)\)
Gọi phương trình đường thẳng d1 qua 2 điểm A; B có dạng:
\(y=mx+n\)
A; B thuộc d1 nên: \(\left\{{}\begin{matrix}3=-m+n\\-3=2m+n\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}m=-2\\n=1\end{matrix}\right.\)
\(\Rightarrow\) Phương trình d1: \(y=-2x+1\)
A;B;C thẳng hàng khi và chỉ khi C thuộc d1
\(\Rightarrow2a-3=-2a+1\)
\(\Rightarrow4a=4\Rightarrow a=1\Rightarrow b=-1\)
\(\Rightarrow a+b=0\)
Giải giùm mình bài này với
tim min : | x - 1 | + | x + 2 | + 5
giải chi tiết giùm mình nha ai giải chi tiết mình tích cho
thế thì hiếm người trả lời đầy đủ cho bn lắm
mọi người ơiii, giúp mình giải bài này vớiii
a: Xét ΔADH vuông tại H và ΔBDA vuông tại A có
\(\widehat{ADH}\) chung
Do đó: ΔADH∼ΔBDA
b: Xét ΔHAD vuông tại H và ΔHBA vuông tại H có
\(\widehat{HAD}=\widehat{HBA}\)
Do đó: ΔHAD∼ΔHBA
Suy ra: HA/HB=HD/HA
hay \(HA^2=HB\cdot HD\)
a) Xét \(\Delta ADH\) và \(\Delta BDA:\)
\(\widehat{H}=\widehat{A}\left(=90^o\right).\)
\(\widehat{D}\) chung.
\(\Rightarrow\Delta ADH\sim\Delta BDA\left(g-g\right).\)
b) Xét \(\Delta BDA\) và \(\Delta BAH:\)
\(\widehat{BAD}=\widehat{BHA}\left(=90^o\right).\)
\(\widehat{B}\) chung.
\(\Rightarrow\Delta BDA\sim\) \(\Delta BAH\left(g-g\right).\)
Mà \(\Delta ADH\sim\Delta BDA\left(cmt\right).\)
\(\Rightarrow\Delta ADH\sim\Delta BAH.\)
\(\Rightarrow\dfrac{AH}{BH}=\dfrac{DH}{AH}\) (2 cạnh tương ứng).
\(\Rightarrow AH^2=DH.BH.\)
giúp mình bài giải chi tiết bài này ạ