Vẽ tam giác ABC có AB=2cmm BC=3cm, CA=4cm và đường tròn (A;2cm). Chứng tỏ rằng tâm của đường tròn đường kính AC nằm trên đường tròn (A;2cm).
Mọi người trả lời đầy đủ giúp mình nhé. Mình đang cần gấp. Cảm ơn rất nhiều!
Cho tam giác ABC vuông tại A có AB = 4cm, AC=3cm, đường cao AH. Vẽ đường tròn tâm C, bán kính CA. Đường thẳng AH cắt đường trong (C) tại điểm thứ 2 là D Cho tam giác ABC vuông tại A có AB=4cm, AC=3cm, đường cao AH. Vẽ đường tròn tâm C, bán kính CA. Đường thẳng AH cắt đường trong (C) tại điểm thứ 2 là D. a) Tính độ dài đoạn thẳng AH b) Chứng minh BD là tiếp tuyến của đường tròn (C) c) Qua C kẻ đường thẳng vuông góc với BC cắt các tia BA,BD thứ tự E,F. Trên cung nhỏ AD của (C) lấy điểm M bất kỳ, qua M kẻ tiếp tuyến với (C) cắt AB,BD lần lượt tại P,Q. Chứng minh EF bình phương =4PE.QF
a:\(BC=\sqrt{4^2+3^2}=5\left(cm\right)\)
AH=4*3/5=2,4cm
b: ΔCAD cân tại C
mà CH là đường cao
nên CH là phân giác của góc ACD
Xét ΔCAB và ΔCDB có
CA=CD
góc ACB=góc DCB
CB chung
Do dó: ΔCAB=ΔCDB
=>góc CDB=90 độ
=>BD là tiếp tuyến của (C)
Cho tam giác ABC có AC = 3cm, AB = 4cm, BC = 5cm. Vẽ đường tròn (C; CA). Khẳng định nào sau đây là đúng?
A.Đường thẳng BC cắt đường tròn (C; CA) tại một điểm
B.AB là cát tuyến của đường tròn (C; CA)
C.AB là tiếp tuyến của (C; CA)
D. BC là tiếp tuyến của (C; CA)
Đáp án C
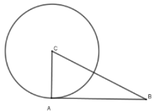
+ Xét tam giác có:
B C 2 = 5 2 = 25 ; A B 2 + A C 2 = 4 2 + 3 2 = 25 ⇒ B C 2 = A B 2 + A C 2
⇒ ΔABC vuông tại A (Định lý Pytago đảo)
⇒ AB ⊥ AC mà A ∈ (C; CA) nên AB là tiếp tuyến của (C; CA)
Cho tam giác ABC có AC = 3cm, AB = 4cm, BC = 5cm. Vẽ đường tròn (C; CA). Khẳng định nào sau đây là đúng?
A.Đường thẳng BC cắt đường tròn (C; CA) tại một điểm
B.AB là cát tuyến của đường tròn (C; CA)
C.AB là tiếp tuyến của (C; CA)
D. BC là tiếp tuyến của (C; CA)
Chọn đáp án C
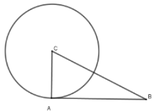
+ Xét tam giác có:
B C 2 = 5 2 = 25 ; A B 2 + A C 2 = 4 2 + 3 2 = 25 ⇒ B C 2 = A B 2 + A C 2
⇒ Δ A B C vuông tại A (Định lý Pytago đảo)
⇒ A B ⊥ A C m à A ∈ (C; CA) nên AB là tiếp tuyến của (C; CA)
cho tam giác abc có ab=3cm, ac=4cm, bc=5cm. kẻ ah vuông góc với bc( h thuộc bc). a/ tam giác abc là tam giác gì? vì sao. b/ tính ah, góc b và c. c/ vẽ đường tròn( b, bh) và đường tròn ( c, ch). từ điểm a lần lượt vẽ tiếp tuyến am và an của đường tròn( b) và (c). tính góc mhn
a. \(BC^2=AB^2+AC^2\) nên ABC vuông tại A
b. Hệ thức lượng: \(AH=\dfrac{AB\cdot AC}{BC}=2,4\left(cm\right)\)
\(\sin B=\dfrac{AC}{BC}=\dfrac{4}{5}\approx\sin53^0\\ \Rightarrow\widehat{B}\approx53^0\\ \Rightarrow\widehat{C}=90^0-\widehat{B}\approx37^0\)
bài 1
a)vẽ tam giác ABC, biết BC=4cm; AB=1,5cm; AC=3cm.
b) vẽ đường tròn (B; BA) và đường tròn (C; CA) chúng cắt nhau tại một điểm thứ hai là D, vẽ các đoạn thẳng BD và CD. Tính chu vi tam giác DBC.
c) đoạn thẳng AB cắt BC tại H. Hỏi trong hình vẽ có tất cả bao nhiêu tam giác?
Vẽ theo yêu cầu đầu bài.
+ Vẽ đoạn AB = 6 cm.
+ Vẽ đường tròn (A; 3cm).
+ Vẽ đường tròn (B; 4cm).
+ Đường tròn (A; 3cm) cắt đường tròn (B; 4cm) tại hai điểm C và D.
+ Tính chu vi tam giác ABC và tam giác ADB.
a/ Vẽ tam giác ABC có AB=3cm; AC=4cm; BC=5cm
b/ Vẽ trung điểm M của cạnh BC. Tính MB,MC
c/ Vẽ đường tròn (M;2,5cm).
d/ Vì sao đường tròn (M;2,5cm) đi qua B và C
Cho tam giác ABC có cạnh AB = 3cm ,cạnh BC = 4cm ,cạnh CA = 5cm , lần lượt lấy trung điểm của các cạnh AB,BC,CA làm tâm vẽ 3 hình tròn có đường kính lần lượt là AB,BC,CA . Tính diện tích phần gạch chéo .
Vẽ đoạn AB=6cm
Vẽ đường tròn[A;3cm]
Vẽ đường tròn [B;4cm]
Đường tròn [A;3cm] cắt [B;4cm] tại C và D
Tính chu vi tam giác ABC và tam giác ADB
Chu vi tam giác ABC là:
6+3+4=13(cm)
Chu vi tam giác ADB là:
6+3+4=13(cm)
ĐS: Chu vi tam giác ABC và tam giác ADB= 13 cm
K CHO MIK NHA