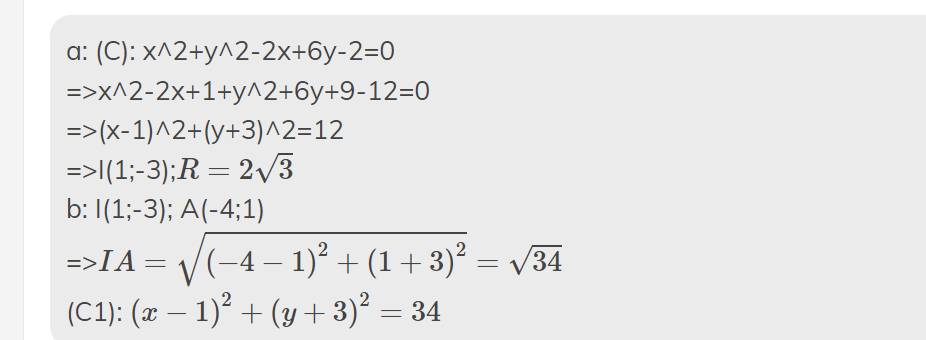Câu 4. (2,0 điểm) Cho đường tròn (0; 2, 5cm) có dây BC = 3c cố định. Trên cung lớn BC lấy điểm A bất kì sao cho tam giác ABC nhọn. Các đường cao BD và CE của tam giác ABC cắt nhau tại H (D in AC E AB). 1) Chứng minh tứ giác BEDC là tứ giác nội tiếp. 2) Kẻ đường kinh AK của đường tròn (O; R) Chứng minh: góc EDB = góc CBK . 3) Tính bán kính đường tròn ngoại tiếp tam giác DEH.
LH
Những câu hỏi liên quan
Cho hàm số y -x² có đổ thị là parabol (P). a) Vẽ parabol (P) trên mặt phẳng tọa độ; b) Viết phương trinh đường thẳng (d), biết rằng (d) cắt parabol (P) tại điểm có hoành độ bằng 2 và cắt trục tung tại điểm có tung độ bằng 1. c) Hãy tìm góc tạo bởi đường thẳng (d) vừa xác định ở câu b) và trục Ox (làm tròn đến độ). Câu 3: (2,0 điểm) Cho phương trình ẩn x, tham số m: x² + (m- 1)x-m 0 a) Chứng minh phương trình luôn có nghiệm với mọi m; b) Tim m để phương trình có hai nghiệm x, X2; X X2 sao cho x...
Đọc tiếp
Cho hàm số y = -x² có đổ thị là parabol (P). a) Vẽ parabol (P) trên mặt phẳng tọa độ; b) Viết phương trinh đường thẳng (d), biết rằng (d) cắt parabol (P) tại điểm có hoành độ bằng 2 và cắt trục tung tại điểm có tung độ bằng 1. c) Hãy tìm góc tạo bởi đường thẳng (d) vừa xác định ở câu b) và trục Ox (làm tròn đến độ). Câu 3: (2,0 điểm) Cho phương trình ẩn x, tham số m: x² + (m- 1)x-m 0 a) Chứng minh phương trình luôn có nghiệm với mọi m; b) Tim m để phương trình có hai nghiệm x, X2; X < X2 sao cho x - 2x = -2. Câu 4: (2,0 điểm) Cho đường tròn (0; 6cm) và A là điểm nằm ngoài đường tròn (0) sao cho OA = 10cm. Qua A về các tiếp tuyến AB, AC với đường tròn (0) (B,C là các tiếp điểm); AO cắt BC tại H. a) Chứng minh tứ giác OBAC nội tiếp được; b) Tính độ dài đoạn thẳng BH; c) Vẽ đường kính BD của đường tròn (0). Chứng minh CD I OA
Câu 3: (2,0 điểm) Cho đường tròn (O,R) và điểm S ở ngoài đường tròn sao cho OS = 2R b.Qua S kẻ cát tuyến SMN( M nằm giữa S và N. M,N không nằm trên đường thẳng SO). 1).Gọi I là trung điểm của MN , chứng minh hat OBI = hat OAI , c)Biết SN = 2, 5R Tĩnh SM theo R? Chứng minh : SN = S * B ^ 2 Vẽ các tiếp tuyến SA,SB với đường tròn (O) a.Chứng minh tứ giác OASB nội tiếp.
a: góc OAS+góc OBS=180 độ
=>OASB nội tiếp
b: ΔOMN cân tại O
mà OI là trung tuyến
nên OI vuông góc IS
góc OIS=góc OAS=góc OBS=90 độ
=>O,A,I,S,B cùng nằm trên đường tròn đường kính OS
=>góc OBI=góc OAI
c: Xet ΔSBM và ΔSNB có
góc SBM=góc SNB
góc NSB chung
=>ΔSBM đồng dạng với ΔSNB
=>SB^2=SM*SN
Đúng 0
Bình luận (0)
Câu 5. (2,0 điểm) Cho Tam giác ABC có ba đỉnh năm trên đường tròn (O). Các đường cao BD, CE cắt nhau tại H (DEAC;EEAB), Vẽ đường kính AK của đường tròn (O).a) Chứng minh rằng: Tứ giác BHCK là hình bình hành. b) Gọi M là trung điểm BC, G là trọng tâm của tam giác ABC. Chứng minh rằng ba điểm H, G, O thẳng hàng.
Đọc tiếp
Câu 5. (2,0 điểm) Cho Tam giác ABC có ba đỉnh năm trên đường tròn (O). Các đường cao BD, CE cắt nhau tại H (DEAC;EEAB), Vẽ đường kính AK của đường tròn (O).
a) Chứng minh rằng: Tứ giác BHCK là hình bình hành. b) Gọi M là trung điểm BC, G là trọng tâm của tam giác ABC. Chứng minh rằng ba điểm H, G, O thẳng hàng.
a: góc ABK=1/2*sđ cung AK=1/2*180=90 độ
=>BK vuông góc AB
=>BK//CH
góc ACK=1/2*sđ cung AK=1/2*180=90 độ
=>CE vuông góc AB
=>CH//BK
mà BK//CH
nên BHCK là hình bình hành
b: Vì M là trung điểm của BC nên M là trung điểm của HK
G là trọng tâm của ΔABC nên AG=2/3AM
=>G là trọng tâm của ΔAHK
=>H,G,O thẳng hàng
Đúng 0
Bình luận (0)
Câu 4: (3,5 điểm). Cho nửa đường tròn (0: R) đườngkinh AB. Trên nữa mặt phảng bở AB chủa nửa đườngtròn, về các tiếp tuyển Ax, By với đường tròn. Qua điểm C bất ki thuộc nửa đường tròn ( C khác A vă B), kẻ tiếptuyển với nửa đường tròn, cất Ar, By lần lưrợt tại Đ và E. 1)Chíng minh rằng: 4AD + BE DE và DOE 90 2) Chứng minh: AD.BE R 3) AC cắt ĐO tại M, BC cát OE tại N. Tử giác CMON là hinh gi? Vi sao? 4) AN cát CO tại H. Khi điểm C di chuyển trên nửa đường tròn (0; R) thì điểm H di chuyển trên...
Đọc tiếp
Câu 4: (3,5 điểm). Cho nửa đường tròn (0: R) đường
kinh AB. Trên nữa mặt phảng bở AB chủa nửa đường
tròn, về các tiếp tuyển Ax, By với đường tròn. Qua điểm
C bất ki thuộc nửa đường tròn ( C khác A vă B), kẻ tiếp
tuyển với nửa đường tròn, cất Ar, By lần lưrợt tại Đ và E.
1)Chíng minh rằng: 4AD + BE = DE và DOE = 90"
2) Chứng minh: AD.BE = R
3) AC cắt ĐO tại M, BC cát OE tại N. Tử giác
CMON là hinh gi? Vi sao?
4) AN cát CO tại H. Khi điểm C di chuyển trên nửa
đường tròn (0; R) thì điểm H di chuyển trên đường
nảo? Vi sao?
Giúp mình giải 3 với 4 với mn
Đúng 0
Bình luận (0)
Câu 4
Cho đường tròn (0) đường kinh AB Điểm 1 năm giữa A và O (1 khác A và 0) Kệ đường thống tuông góc với AB tại 1, đường thông này cắt đường tròn (O) tại M và N. Gọi S là giao điểm của hai đường thẳng BM vĩ AN, Qua 5 kế đường thẳng song song với NỀN, đường thẳng này cắt các đường thắng AB và AM lần lượt tại lì và l a) Chứng minh rằng từ giác SXAM nội tiếp
c) Chứng minh rằng KM là tiếp tuyên của đường tròn (0)
ở Chm minh rêu: 3 điểm EN Ething line
b) Chứng minh rằng SA SNSB.SM
Đọc tiếp
Câu 4 Cho đường tròn (0) đường kinh AB Điểm 1 năm giữa A và O (1 khác A và 0) Kệ đường thống tuông góc với AB tại 1, đường thông này cắt đường tròn (O) tại M và N. Gọi S là giao điểm của hai đường thẳng BM vĩ AN, Qua 5 kế đường thẳng song song với NỀN, đường thẳng này cắt các đường thắng AB và AM lần lượt tại lì và l a) Chứng minh rằng từ giác SXAM nội tiếp c) Chứng minh rằng KM là tiếp tuyên của đường tròn (0) ở Chm' minh rêu: 3 điểm EN Ething line b) Chứng minh rằng SA SN=SB.SM
Câu 20: Trong mặt phăng tọa độ Oxy, cho điểm I(4;3), đường thăng d:3x+4y-4=0 và đường tròn (C):x²+y²-2x+6y-2=0.
a) Tìm tọa độ tâm và bán kính R của đường tròn (C).
b) Viết phương trình đường tròn có tâm I và đi qua A(-4;1)
c) Viết phương trình đườNg tròn (C') có tâm là I và cắt d tại hai điếm M, N sao cho MN =6
a) Để tìm tọa độ tâm và bán kính của đường tròn ©, ta cần viết lại phương trình của nó dưới dạng chuẩn:
\begin{align*}
x^2 + y^2 - 2x + 6y - 2 &= 0 \
\Leftrightarrow (x-1)^2 + (y+3)^2 &= 14
\end{align*}
Vậy, tọa độ tâm của đường tròn © là $(1,-3)$ và bán kính của đường tròn © là $\sqrt{14}$.
b) Đường tròn có tâm $I(4,3)$ và đi qua $A(-4,1)$ có phương trình là:
$$(x-4)^2 + (y-3)^2 = (-4-4)^2 + (1-3)^2 = 20$$
c) Để tìm phương trình đường tròn (C') có tâm là $I(4,3)$ và cắt đường thẳng $d: 3x+4y-4=0$ tại hai điểm $M$ và $N$ sao cho $MN=6$, ta có thể làm như sau:
Tìm giao điểm $H$ của đường thẳng $d$ và đường vuông góc với $d$ đi qua $I$.Tìm hai điểm $M$ và $N$ trên đường thẳng $d$ sao cho $HM=HN=3$.Xây dựng đường tròn (C') có tâm là $I$ và bán kính bằng $IN=IM=\sqrt{3^2+4^2}=5$.
Để tìm giao điểm $H$, ta cần tìm phương trình của đường thẳng vuông góc với $d$ đi qua $I$. Đường thẳng đó có phương trình là:
$$4x - 3y - 7 = 0$$
Giao điểm $H$ của đường thẳng này và $d$ có tọa độ là $(\frac{52}{25}, \frac{9}{25})$.
Để tìm hai điểm $M$ và $N$, ta có thể sử dụng công thức khoảng cách giữa điểm và đường thẳng. Khoảng cách từ điểm $H$ đến đường thẳng $d$ là:
$$d(H,d) = \frac{|3\cdot \frac{52}{25} + 4\cdot \frac{9}{25} - 4|}{\sqrt{3^2+4^2}} = \frac{1}{5}$$
Vậy, hai điểm $M$ và $N$ cách $H$ một khoảng bằng $\frac{3}{5}$ và $\frac{4}{5}$ đơn vị theo hướng vuông góc với $d$. Ta có thể tính được tọa độ của $M$ và $N$ như sau:
$$M = \left(\frac{52}{25} - \frac{4}{5}\cdot 4, \frac{9}{25} + \frac{3}{5}\cdot 3\right) = \left(\frac{12}{25}, \frac{54}{25}\right)$$
và
$$N = \left(\frac{52}{25} + \frac{4}{5}\cdot 4, \frac{9}{25} + \frac{4}{5}\cdot 3\right) = \left(\frac{92}{25}, \frac{27}{5}\right)$$
Cuối cùng, phương trình đường tròn (C') có tâm là $I(4,3)$ và cắt đường thẳng $d$ tại hai điểm $M$ và $N$ sao cho $MN=6$ là:
$$(x-4)^2 + (y-3)^2 = 5^2$$
Đúng 0
Bình luận (0)
Câu 20: Trong mặt phăng tọa độ Oxy, cho điểm I(4;3), đường thăng d:3x+4y-4=0 và đường tròn (C):x²+y²-2x+6y-2=0.
a) Tìm tọa độ tâm và bán kính R của đường tròn (C).
b) Viết phương trình đường tròn có tâm I và đi qua A(-4;1)
c) Viết phương trình đườNg tròn (C') có tâm là I và cắt d tại hai điếm M, N sao cho MN =6
Giải thích cụ thể câu c cho mình.
a: (C): x^2+y^2-2x+6y-2=0
=>x^2-2x+1+y^2+6y+9-12=0
=>(x-1)^2+(y+3)^2=12
=>I(1;-3);\(R=2\sqrt{3}\)
b: I(1;-3); A(-4;1)
=>\(IA=\sqrt{\left(-4-1\right)^2+\left(1+3\right)^2}=\sqrt{34}\)
(C1): \(\left(x-1\right)^2+\left(y+3\right)^2=34\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Câu 20: Trong mặt phăng tọa độ Oxy, cho điểm I(4;3), đường thăng d:3x+4y-4=0 và đường tròn (C):x²+y²-2x+6y-2=0.
a) Tìm tọa độ tâm và bán kính R của đường tròn (C).
b) Viết phương trình đường tròn có tâm I và đi qua A(-4;1)
c) Viết phương trình đườNg tròn (C') có tâm là I và cắt d tại hai điếm M, N sao cho MN =6
Giải thích cụ thể câu c cho mình.
Bài 4. (3,5 điểm) Cho điểm M nằm ngoài đường tròn (0;R) sao cho OM = 2R. Từ M kẻ các tiếp tuyến MA, MB với đường tròn (0) (A, B là các tiếp điểm). Kẻ đường kính AC của đường tròn (0). Gọi H là giao điểm của AB và OM. 1) Chứng minh bốn điểm A, O, B, M cùng thuộc một đường tròn. 2) Tính tỷ số OH/OM. 3) Gọi E là giao điểm của CM và đường tròn (0). Chứng minh HE vuông góc BE.