 Giúp e với m.n ạaaa
Giúp e với m.n ạaaa
H24
Những câu hỏi liên quan
 Giúp với m.n ạaaa
Giúp với m.n ạaaa
Giúp e với ạaaa. E c.ơn trước
a) a//b vì c cắt a và b vông góc tại điểm A và B
Đúng 0
Bình luận (0)
Vì C1 và C2 là hai cặp góc đối đỉnh
⇒ C1=C2 (45o)
Đúng 1
Bình luận (0)
a, Vì a⊥c và b⊥c nên a//b
b, Ta có \(\widehat{C_1}=\widehat{C_2}=54^0\) (đối đỉnh)
Mà a//b nên \(\widehat{D_1}=180^0-\widehat{C_1}=126^0\) (trong cùng phía)
c, Vì a//b nên \(\widehat{C_1}=\widehat{MDN}=54^0\)
Xét tam giác MND có \(\widehat{NMD}=180^0-\widehat{N_1}-\widehat{MDN}=180^0-36^0-54^0=90^0\)
Vậy CM⊥MN
Đúng 1
Bình luận (0)
Giúp e với ạaaa
Lời giải:
a. Để $f(x)=x^2-2mx+3m+4\geq 0$ với mọi $x\in\mathbb{R}$ thì:
\(\left\{\begin{matrix}
a=1>0\\
\Delta'=m^2-3m-4\leq 0\end{matrix}\right.\Leftrightarrow m^2-3m-4\leq 0\)
$\Leftrightarrow (m+1)(m-4)\leq 0$
$\Leftrightarrow -1\leq m\leq 4$
b.
Để pt có 2 nghiệm pb cùng dấu thì:
\(\left\{\begin{matrix}
\Delta'=m^2-3m-4>0\\
P=3m+4>0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix}
(m+1)(m-4)> 0\\
m> \frac{-4}{3}\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix}
m> 4 \text{hoặc} m< -1\\
m> \frac{-4}{3}\end{matrix}\right.\)
$\Leftrightarrow m>4$ hoặc $\frac{-4}{3}< m < -1$
Đúng 1
Bình luận (0)
Lời giải:
a. Để $f(x)=x^2-2mx+3m+4\geq 0$ với mọi $x\in\mathbb{R}$ thì:
\(\left\{\begin{matrix}
a=1>0\\
\Delta'=m^2-3m-4\leq 0\end{matrix}\right.\Leftrightarrow m^2-3m-4\leq 0\)
$\Leftrightarrow (m+1)(m-4)\leq 0$
$\Leftrightarrow -1\leq m\leq 4$
b.
Để pt có 2 nghiệm pb cùng dấu thì:
\(\left\{\begin{matrix}
\Delta'=m^2-3m-4>0\\
P=3m+4>0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix}
(m+1)(m-4)> 0\\
m> \frac{-4}{3}\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix}
m> 4 \text{hoặc} m< -1\\
m> \frac{-4}{3}\end{matrix}\right.\)
$\Leftrightarrow m>4$ hoặc $\frac{-4}{3}< m < -1$
giúp e với ạaaa
Đọc tiếp
giúp e với ạaaa
Gọi chữ số hàng chục là x và chữ số hàng đơn vị là y (x;y là các chữ số từ 0 đến 9)
Do chữ số hàng chục hơn chữ số hàng đơn vị là 4
\(\Rightarrow x-y=4\)
Giá trị chữ số ban đầu: \(10x+y\)
Giá trị chữ số sau khi đổi chỗ: \(10y+x\)
Do tổng số mới và số cũ là 132 nên ta có pt:
\(10x+y+10y+x=132\Rightarrow11\left(x+y\right)=132\Rightarrow x+y=12\)
Ta được hệ: \(\left\{{}\begin{matrix}x-y=4\\x+y=12\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=8\\y=4\end{matrix}\right.\)
Vậy số đó là 84
Đúng 1
Bình luận (1)
 Giải giúp e với ạaaa
Giải giúp e với ạaaa
Gọi số học sinh nam và số học sinh nữ lần lượt là a,b
Theo đề, ta có: a+b=46 và 2a+3b=118
=>a=20 và b=26
Đúng 0
Bình luận (0)
 Giúp e 6,7 với ạaaa
Giúp e 6,7 với ạaaa
 Giúp e với ạaaa hleppppppp
Giúp e với ạaaa hleppppppp
Gọi giao của AO với (O) là D
=>AD=2R
ΔACD nội tiếp đường tròn đường kính AD
=>ΔACD vuông tại C
mà CB vuông góc AD
nên CB^2=AB*BD
=>CB^2=AB(2*R-AB)
=>1,1(2*R-1,1)=28,4^2
=>R=367,2m
=>AD=734,4(m)
\(AC=\sqrt{1.1^2+28.4^2}=28,42\left(m\right)\)
OA=OC=367,2m
\(cosAOC=\dfrac{OA^2+OC^2-AC^2}{2\cdot OA\cdot OC}\simeq0.998\)
=>góc AOC=4 độ
=>sđ cung AC=4 độ
Đúng 0
Bình luận (0)
M={xE Z|x có tận cùng 2 và -15<x_< 32
giúp e vs ạ, e thank you trc ạaaa
M = { -12; -2; ...; 22; 32}
Đúng 1
Bình luận (0)
Giúp mik với ạaaa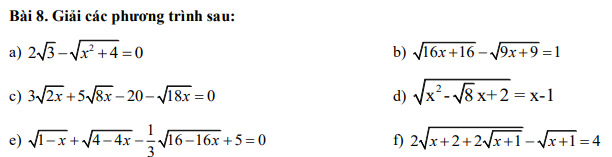
a.
$2\sqrt{3}-\sqrt{x^2+4}=0$
$\Leftrightarrow 2\sqrt{3}=\sqrt{x^2+4}$
$\Leftrightarrow 12=x^2+4$
$\Leftrightarrow 8=x^2$
$\Leftrightarrow x=\pm 2\sqrt{2}$
b. ĐKXĐ: $x\geq -1$
$\sqrt{16(x+1)}-\sqrt{9(x+1)}=1$
$\Leftrightarrow 4\sqrt{x+1}-3\sqrt{x+1}=1$
$\Leftrightarrow \sqrt{x+1}=1$
$\Leftrightarrow x+1=1$
$\Leftrightarrow x=0$ (tm)
c. ĐKXĐ: $x\geq 0$
$3\sqrt{2x}+5\sqrt{8x}-20-\sqrt{18x}=0$
$\Leftrightarrow 3\sqrt{2x}+10\sqrt{2x}-20-3\sqrt{2x}=0$
$\Leftrightarrow 10\sqrt{2x}-20=0$
$\Leftrightarrow \sqrt{2x}=2$
$\Leftrightarrow 2x=4$
$\Leftrightarrow x=2$ (tm)
Đúng 0
Bình luận (0)
d.
PT \(\Rightarrow \left\{\begin{matrix} x-1\geq 0\\ x^2-\sqrt{8x}+2=(x-1)^2\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x\geq 1\\ x=\frac{1+\sqrt{2}}{2}\end{matrix}\right.\Leftrightarrow x=\frac{1+\sqrt{2}}{2}\)
e. ĐKXĐ: $x\leq 1$
PT $\Leftrightarrow \sqrt{1-x}+2\sqrt{1-x}-\frac{4}{3}\sqrt{1-x}+5=0$
$\Leftrightarrow \frac{5}{3}\sqrt{1-x}=-5< 0$ (vô lý)
Vậy pt vô nghiệm.
f. ĐKXĐ: $x\geq -1$
PT $\Leftrightarrow 2\sqrt{(\sqrt{x+1}+1)^2}-\sqrt{x+1}=4$
$\Leftrightarrow 2(\sqrt{x+1}+1)-\sqrt{x+1}=4$
$\Leftrightarrow \sqrt{x+1}=2$
$\Leftrightarrow x=3$ (tm)
Đúng 0
Bình luận (0)
a) Ta có: \(2\sqrt{3}-\sqrt{x^2+4}=0\)
\(\Leftrightarrow\sqrt{x^2+4}=2\sqrt{3}\)
\(\Leftrightarrow x^2+4=12\)
\(\Leftrightarrow x^2=8\)
hay \(x\in\left\{2\sqrt{2};-2\sqrt{2}\right\}\)
b) Ta có: \(\sqrt{16x+16}-\sqrt{9x+9}=1\)
\(\Leftrightarrow4\sqrt{x+1}-3\sqrt{x+1}=1\)
\(\Leftrightarrow\sqrt{x+1}=1\)
\(\Leftrightarrow x+1=1\)
hay x=0
Đúng 0
Bình luận (0)
Xem thêm câu trả lời





