giả sử x1,x2 là 2 nghiệm của phương trình : x2-2x-2=0
cmr: m= x1^2015+ x2^2015 là 1 số nguyên
Giả sử phương trình log 2 2 x - ( m + 2 ) log 2 x + 2 m = 0 có hai nghiệm thực phân biệt x 1 , x 2 thỏa mãn x 1 + x 2 = 6 . Giá trị của biểu thức x 1 - x 2 là
A. 3
B. 8
C. 2
D. 4
Chọn đáp án C
Phương pháp
+) Đặt điều kiện để phương trình có nghĩa.
+) Đặt ẩn phụ để giải phương trình: log 2 x = t . Tìm điều kiện để phương trình có nghiệm.
+) Dựa vào dữ kiện x 1 + x 2 = 6 tìm m. Từ đó tính x 1 - x 2 .
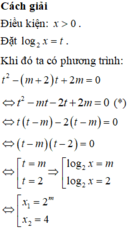
Phương trình đã cho có hai nghiệm phân biệt: x 1 , x 2 ⇔ phương trình (*) có hai nghiệm phân biệt ⇔ m ≠ 2 .
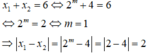
Giả sử x 1 , x 2 là hai nghiệm của phương trình x 2 + px + q = 0. Hãy lập một phương trình bậc hai có hai nghiệm x 1 + x 2 , x 1 x 2
Giả sử x 1 , x 2 la hai nghiệm của phương trình x 2 + px + q = 0
Theo hệ thức Vi-ét ta có: x 1 + x 2 = - p/1 = - p; x 1 x 2 = q/1 = q
Phương trình có hai nghiệm là x 1 + x 2 và x 1 x 2 tức là phương trình có hai nghiệm là –p và q.
Hai số -p và q là nghiệm của phương trình.
(x + p)(x - q) = 0 ⇔ x 2 - qx + px - pq = 0 ⇔ x 2 + (p - q)x - pq = 0
Phương trình cần tìm: x 2 + (p - q)x - pq = 0
Giả sử x 1 , x 2 là nghiệm của phương trình x 2 - m + 2 x + m 2 + 1 = 0 . Khi đó giá trị lớn nhất của biểu thức P = 4 x 1 + x 2 - x 1 x 2 bằng
A. 95 9
B. 11
C. 7
D. - 1 9
Cho phương trình bậc 2 x^2- 2( m-1) x+m^2=0
1.Tìm m để:
A.Pt có hai nghiệm phân biệt
B. PT có một nghiệm là -2
2. Giả sử X1, x2 là 2 nghiệm của PT. cmt (x1-x2) ^2+4(x1+x2) +4=0
Giả sử phương trình 2 x 2 − 4 m x − 1 = 0 (với m là tham số) có hai nghiệm x 1 , x 2 . Tìm giá trị nhỏ nhất của biểu thức T = x 1 − x 2
A. min T = 2 3
B. min T = 2
C. min T = 2
D. min T = 2 2
Phương trình 2 x 2 - 4 m x - 1 = 0 có ∆ ' = 4 m 2 + 2 > 0 nên phương trình có hai nghiệm phân biệt x 1 , x 2 với S = x 1 + x 2 = 2 m , P = x 1 x 2 = - 1 2
Ta có: T 2 = x 1 - x 2 2 = S 2 - 4 P = 4 m 2 + 2 ≥ 2 ⇒ T ≥ 2
Dấu bằng xảy ra khi m = 0.
Vậy m i n T = 2
Đáp án cần chọn là: B
Cho phương trình x2 -2mx - 3m2 + 4m -2 = 0
CMR phương trình luôn có 2 nghiệm phân biệt
Tìm m để A = | x1 - x2| có GTNN
Lời giải:
Có: $\Delta'=m^2-(-3m^2+4m-2)=4m^2-4m+2=(2m-1)^2+1\geq 1>0$ với mọi $m\in\mathbb{R}$
Do đó pt luôn có 2 nghiệm phân biệt với mọi $m$.
Khi đó, áp dụng định lý Viet với $x_1,x_2$ là 2 nghiệm của pt thì:
$x_1+x_2=2m$
$x_1x_2=-3m^2+4m-2$
Khi đó:
$A=|x_1-x_2|=\sqrt{(x_1-x_2)^2}=\sqrt{(x_1+x_2)^2-4x_1x_2}$
$=\sqrt{(2m)^2-4(-3m^2+4m-2)}=2\sqrt{(2m-1)^2+1}\geq 2\sqrt{1}=2$
Vậy $A_{\min}=2$. Giá trị này đạt tại $2m-1=0\Leftrightarrow m=\frac{1}{2}$
Giả sử phương trình x^2+mx+n+1=0 có các nghiệm x1,x2 là các số nguyên khác 0. Chứng minh m^2 +n^2 là 1 hợp số
Cho phương trình x^2-2*(m-1)+2 *m-5=0 , với m là tham số Gọi x1 x2 là 2 nghiệm của phương trình trên , tìm tất cả cá giá trị nghuyên dương của m để biểu thức B= (x1/x2)^2+(x2/x1)^2 nhận giá trị nguyên
Δ=(2m-2)^2-4(2m-5)
=4m^2-8m+4-8m+20
=4m^2-16m+24
=4m^2-16m+16+8=(2m-4)^2+8>=8>0 với mọi m
=>Phương trình luôn có hai nghiệm phân biệt
\(B=\dfrac{x_1^2}{x^2_2}+\dfrac{x_2^2}{x_1^2}\)
\(=\dfrac{x_1^4+x_2^4}{\left(x_1\cdot x_2\right)^2}=\dfrac{\left(x_1^2+x_2^2\right)^2-2\left(x_1\cdot x_2\right)^2}{\left(x_1\cdot x_2\right)^2}\)
\(=\dfrac{\left[\left(2m-2\right)^2-2\left(2m-5\right)\right]^2-2\left(2m-5\right)^2}{\left(2m-5\right)^2}\)
\(=\dfrac{\left(4m^2-8m+4-4m+10\right)^2}{\left(2m-5\right)^2}-2\)
\(=\left(\dfrac{4m^2-12m+14}{2m-5}\right)^2-2\)
\(=\left(\dfrac{4m^2-10m-2m+5+9}{2m-5}\right)^2-2\)
\(=\left(2m-1+\dfrac{9}{2m-5}\right)^2-2\)
Để B nguyên thì \(2m-5\in\left\{1;-1;3;-3;9;-9\right\}\)
=>\(m\in\left\{3;2;4;1;7\right\}\)
Cho phương trình x 2 - 2 ( m - 1 ) x + m 2 - 3 m = 0 Giả sử phương trình có hai nghiệm x 1 ; x 2 .Tìm hệ thức giữa x 1 ; x 2 độc lập đối với m.
![]()
![]()
![]()
![]()
Đáp án: A
Theo hệ thức Vi-ét ta có: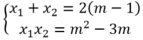
Ta xét các phương án:
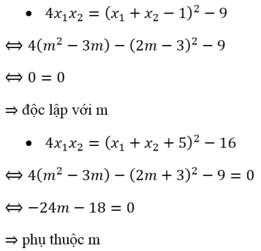
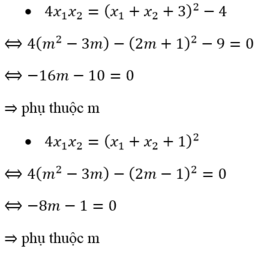
Giả sử phương trình x^2 +mx+n+1=0 có các nghiệm x1,x2 là các số nguyên khác 0. Chứng minh rằng m^2 +n^2 là 1 hợp số
Giup minh vs: https://olm.vn/hoi-dap/question/1269512.html