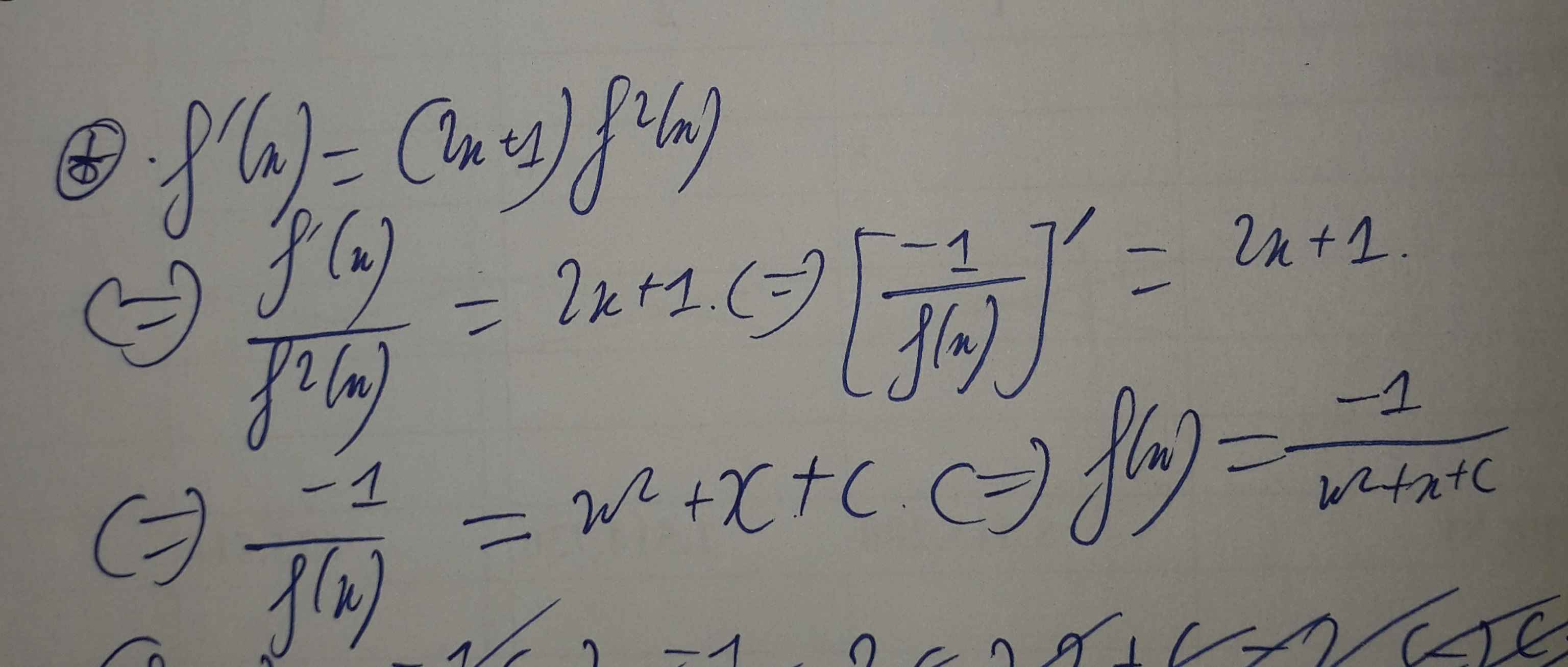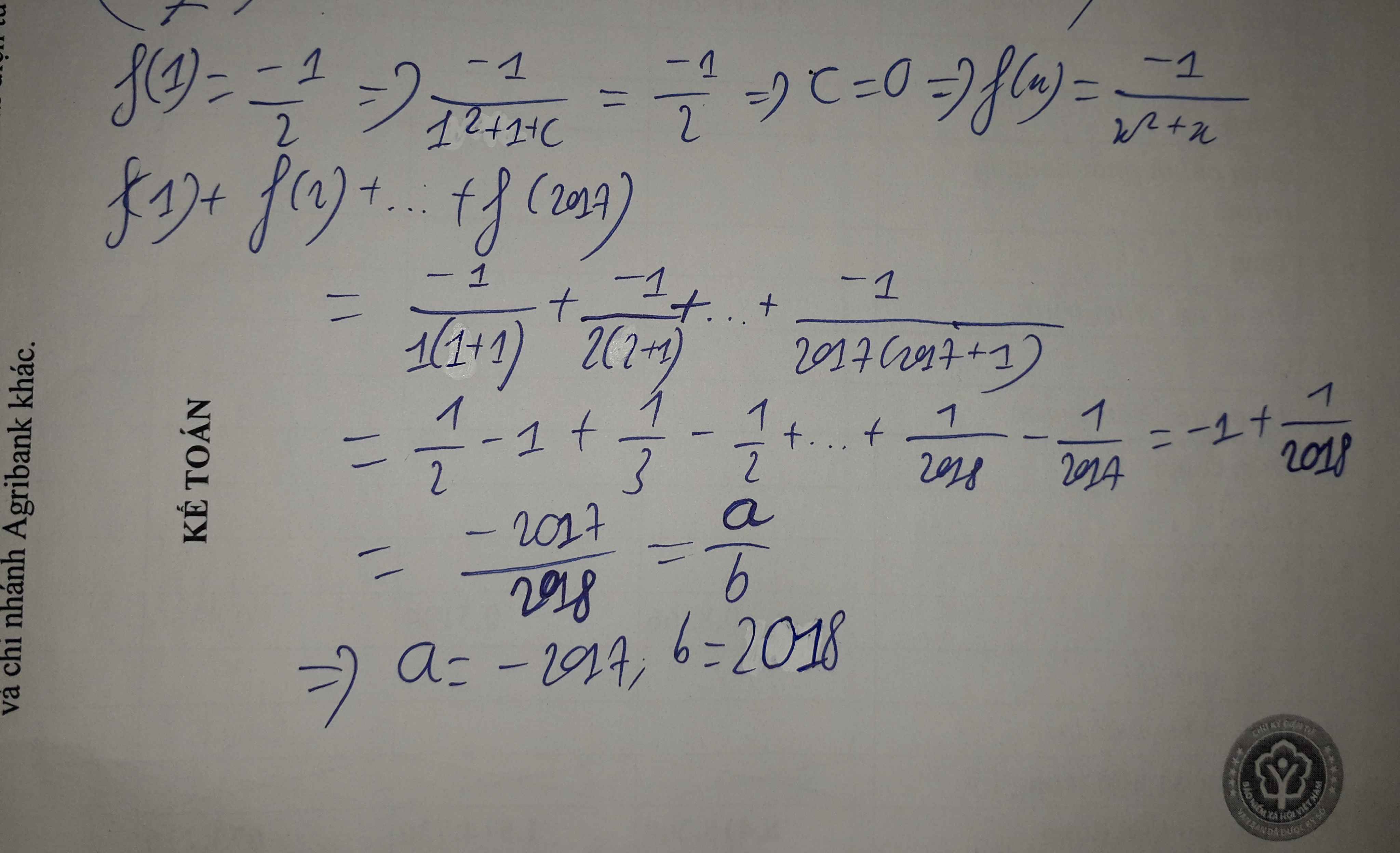Cho f(x) = a x + b .Tìm a,b biết f(1) = -1 và f(-2) = 8
H24
Những câu hỏi liên quan
a) Cho f(x) = a x + b .Tìm a,b biết f(0) = 3 và f(2) = -1
b) Cho f(x) = a x + b .Tìm a,b biết f(1) = -1 và f(-2) = 8
c) Cho f(x) = a x + b .Tìm a,b biết f(0) = 1 và f(-2) = -9
Cho f(x) = a x + b .Tìm a,b biết f(1) = -1 và f(-2) = 8
a+b=-1
-2a+b=8
=>3a=-9
=>a=-3
=>b=-1-(-3)=2
-2a+b=8
=>3a=-9
=>a=-3
=>b=-1-(-3)=2
Đúng 0
Bình luận (0)
Ta có: f(1)=-1
\(\Leftrightarrow a\cdot1+b=-1\)
\(\Leftrightarrow a+b=-1\)(1)
Ta có: f(-2)=8
\(\Leftrightarrow a\cdot\left(-2\right)+b=8\)
\(\Leftrightarrow-2a+b=8\)(2)
Từ (1) và (2) ta lập được hệ phương trình:
\(\left\{{}\begin{matrix}a+b=-1\\-2a+b=8\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3a=-9\\a+b=-1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=-3\\b-3=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-3\\b=2\end{matrix}\right.\)
Vậy: a=-3; b=2
Đúng 0
Bình luận (0)
: Cho đa thức f(x) = ax + b a) Biết f(0) = 3; f(2) = 7, tìm a, b và xác định f(x). b) Biết f(2) = 8; f(– 2) = 12, tìm a, b và xác định f(x)
: Cho đa thức f(x) = ax + b a) Biết f(0) = 3; f(2) = 7, tìm a, b và xác định f(x). b) Biết f(2) = 8; f(– 2) = 12, tìm a, b và xác định f(x) Giiusp mình với ạ
1)Cho đa thức:
f(x)=a+b(x-1). Tìm a,b biết x=0 là một nghiệm và f(1)=5
2)Cho đa thức f(x)=a+b(x-1)+x(x-1).Tìm a,b,c biết f(1)=2,f(0)=3 và 2 là một nghiệm của đa thức f(x)
giúp mình vs nha
cho f(x)=ax+b (a,b là các số, a khác 0)
tìm a, b biết f(1)=2 và f(3)=8
Ta có: f(1)=a+b=2 (1)
f(3)=3a+b=8 (2)
Lấy vế (2) trừ cho vế (1) ta được :
3a+b-a-b= 8-2
2a = 6
=> a = 3
Thay a = 3 vào vế (1) ta được :
3 + b = 2
=> b = 2 - 3 = -1
Vậy a = 3; b = -1
Đúng 0
Bình luận (0)
a) Cho f(x) = a x + b .Tìm a,b biết f(0) = 3 và f(2) = -1
b) Cho f(x) = a x + b .Tìm a,b biết f(1) = -1 và f(-2) = 8
c) Cho f(x) = a x + b .Tìm a,b biết f(0) = 1 và f(-2) = -9
cho hàm số y = f(x) xác định và f(x) \(\ne0\) \(\forall x\in\left(0;+\infty\right)\), \(f'\left(x\right)=\left(2x+1\right)f^2\left(x\right)\) và f(1) = -1/2. Biết tổng f(1) + f(2) + f(3) + ... + f(2017) = a/b (a,b\(\in R\)) với a/b tối giản. Tìm a,b
1)cho f(x)ax^3+bx^2+cx+d trong đó a,b,c,d thuộc Z và thỏa mãn b3a+c.Chứng minh rằng f(1).f(-2) là bình phương của một số nguyên.2)cho đa thức f(x)ax^2+bx+c với a,b,c là hằng số.Hãy xác định a,b,c biết f(1)4,f(-1)8 và a-c43)cho f(x)ax^3+4x(x^2-1)+8;g(x)x^3-4x(bx-1)+c-3.Xác định a,b,c để f(x)g(x).4)cho f(x)cx^2+bx+a và g(x)ax^2+bx+c.cmr nếu Xo là nghiệm của f(x) thì 1/Xo là nghiệm của g(x)5)cho đa thức f(x) thỏa mãn xf(x+2)(x^2-9)f(x).cmr đa thức f(x) có ít nhất 3 nghiệm6)tính f(2) biết f(x)+(x+1)...
Đọc tiếp
1)cho f(x)=ax^3+bx^2+cx+d trong đó a,b,c,d thuộc Z và thỏa mãn b=3a+c.Chứng minh rằng f(1).f(-2) là bình phương của một số nguyên.
2)cho đa thức f(x)=ax^2+bx+c với a,b,c là hằng số.Hãy xác định a,b,c biết f(1)=4,f(-1)=8 và a-c=4
3)cho f(x)=ax^3+4x(x^2-1)+8;g(x)=x^3-4x(bx-1)+c-3.Xác định a,b,c để f(x)=g(x).
4)cho f(x)=cx^2+bx+a và g(x)=ax^2+bx+c.
cmr nếu Xo là nghiệm của f(x) thì 1/Xo là nghiệm của g(x)
5)cho đa thức f(x) thỏa mãn xf(x+2)=(x^2-9)f(x).cmr đa thức f(x) có ít nhất 3 nghiệm
6)tính f(2) biết f(x)+(x+1)f(-x)=x+2