Chọn thẻ ghi phép tính thích hợp cho mỗi hộp:
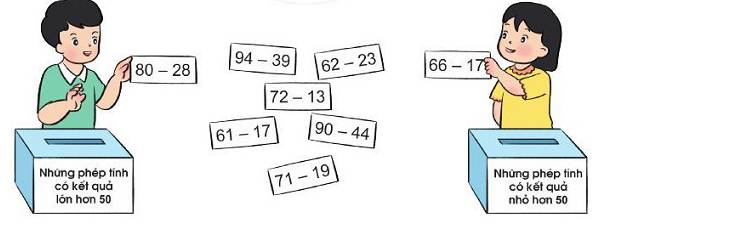
Chọn thẻ ghi phép chia thích hợp cho mỗi ngôi nhà:
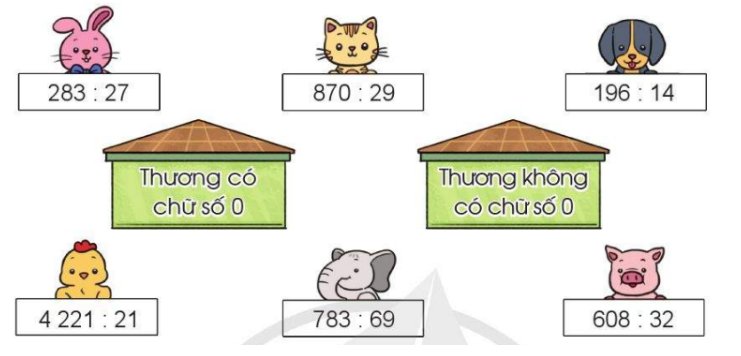
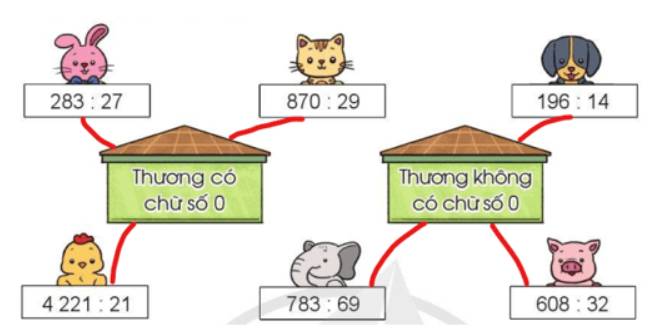
Ta có:
283 : 27 = 10 (dư 13)
870 : 29 = 30
196 : 14 = 14
4 221 : 21 = 201
783 : 69 = 11 (dư 24)
608 : 32 = 19
a) Uớc lượng tính rồi chọn thẻ ghi phép tính thích hợp với mỗi hộp:
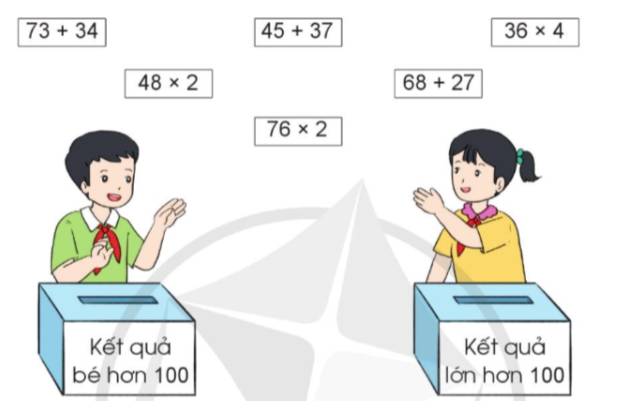
b) Tính để kiểm tra kết quả ước lượng ở câu a.
a) Chỉ ra phép tính có kết quả sai và sửa lại cho đúng:
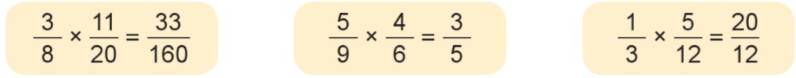
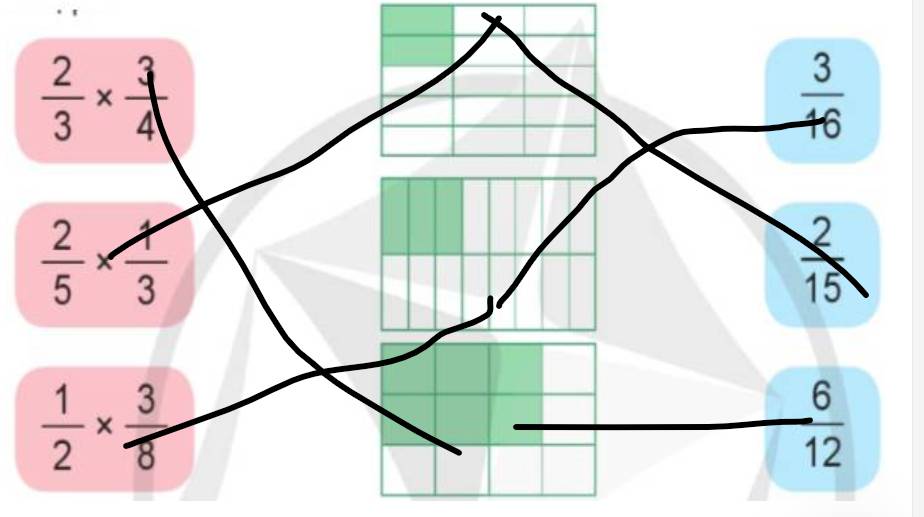
b) Ghép thẻ ghi phép nhân phân số với thẻ hình và thẻ ghi kết quả thích hợp:
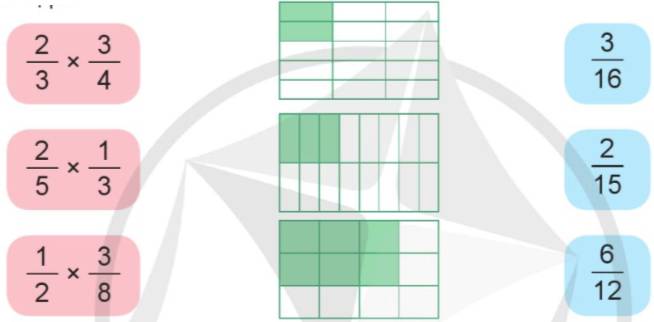
a: \(\dfrac{5}{9}\cdot\dfrac{4}{6}=\dfrac{5\cdot4}{9\cdot6}=\dfrac{20}{54}=\dfrac{10}{27}\)
\(\dfrac{1}{3}\cdot\dfrac{5}{12}=\dfrac{1\cdot5}{3\cdot12}=\dfrac{5}{36}\)
b:
Chọn thẻ ghi cân nặng thích hợp với mỗi con vật sau:
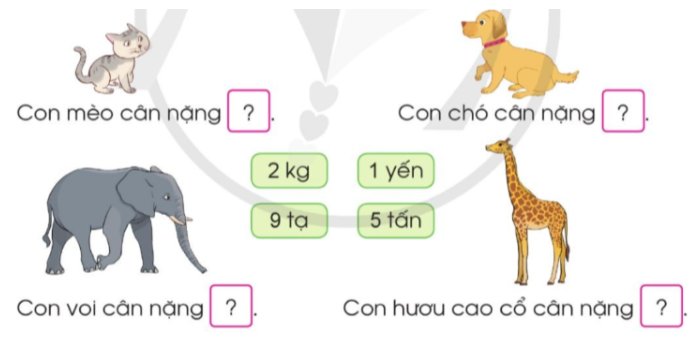
Mèo: 2 kg
Voi: 5 tấn
Chó: 1 yến
Hươu cao cổ: 9 tạ
Con mèo cân nặng 20 kg.
Con chó nặng 1 yến
Con voi nặng 5 tấn.
Con hươu cao cổ nặng 9 tạ.
Chọn thẻ ghi cân nặng thích hợp với mỗi hình vẽ sau:
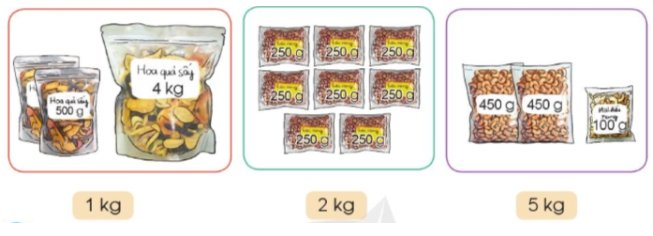
`a, 5kg.`
`b, 2kg`
`c, 1 kg`
Một hộp có 12 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3,…, 12; hai thẻ khác nhau thì ghi hai số khác nhau. Rút ngẫu nhiên một thẻ trong hộp. Xét biến cố “Số xuất hiện trên thẻ được rút ra1 số là hợp số”. Tính xác suất của biến cố trên
n(omega)=12
A={4;6;9;10;12}
=>n(A)=5
=>P(A)=5/12
Từ một hộp có 1000 thẻ được đánh số từ 1 đến 1000. Chọn ngẫu nhiên ra hai thẻ. Tính xác suất để chọn được hai thẻ sao cho tổng của các số ghi trên hai thẻ nhỏ hơn 700.
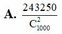
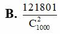
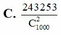
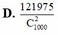
Từ một hộp có 1000 thẻ được đánh số từ 1 đến 1000. Chọn ngẫu nhiên ra hai thẻ. Tính xác suất để chọn được hai thẻ sao cho tổng của các số ghi trên hai thẻ nhỏ hơn 700
A. 243250 C 1000 2
B. 121801 C 1000 2
C. 243253 C 1000 2
D. 121975 C 1000 2
Cho tập hợp A={1;2;3;...;10}. Chọn ngẫu nhiên 3 số từ A. Tính xác suất để 3 số chọn ra ko có 2 số nào là 2 số nguyên liên tiếp.
Một hộp đụng 10 thẻ được đánh số từ 1 đến 10. Phải rút ra ít nhất k thẻ để xác suất có ít nhất1 thẻ ghi số chia hết cho 4 lớn hơn 13/15. Tính k
a. Không gian mẫu: \(C_{10}^3\)
Số cách chọn 3 số nguyên liên tiếp: 8 cách (123; 234;...;8910)
Số cách chọn ra 3 số trong đó có đúng 2 số nguyên liên tiếp:
- Cặp liên tiếp là 12 hoặc 910 (2 cách): số còn lại có 7 cách chọn
- Cặp liên tiếp là 1 trong 7 cặp còn lại: số còn lại có 6 cách chọn
Vậy có: \(C_{10}^3-\left(8+2.7+7.6\right)=56\) bộ thỏa mãn
Xác suất: \(P=\dfrac{56}{C_{10}^3}=...\)
b.
Có 2 số chia hết cho 4 là 4 và 8
Rút ra k thẻ: \(C_{10}^k\) cách
Số cách để trong k thẻ có ít nhất 1 thẻ chia hết cho 4: \(C_{10}^k-C_8^k\)
Xác suất thỏa mãn: \(P=\dfrac{C_{10}^k-C_8^k}{C_{10}^k}>\dfrac{13}{15}\)
\(\Leftrightarrow\dfrac{2}{15}>\dfrac{C_8^k}{C_{10}^k}=\dfrac{\dfrac{8!}{k!\left(8-k\right)!}}{\dfrac{10!}{k!\left(10-k\right)!}}=\dfrac{\left(9-k\right)\left(10-k\right)}{90}\)
\(\Leftrightarrow\left(9-k\right)\left(10-k\right)-12< 0\Leftrightarrow k^2-19k+78< 0\)
\(\Rightarrow6< k< 13\)