Giúp mk cái bài hình kia trong trường hợp vuông góc SC với
MN
Những câu hỏi liên quan
Bài 5. Cho hình chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông cạnh a. Mặt bên hợp với đáy một góc . Tính VS ABCD . theo a và . Bài 6. Tính thể tích khối chóp tứ giác đều S.ABCD có cạnh đáy bằng a và góc ASB α . Áp dụng: Tính VS ABCD . trong trường hợp α 60 độ. Bài 7. Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, góc ABC 120độ . Cho SA vuông góc với đáy và SC 2a .Tính thể tích hình chóp S.ABCD.Bài 8. Cho hình chóp S.ABCD có đáy ABCD là một hình thang cân (AB//CD) với AC20 cm BC...
Đọc tiếp
Bài 5. Cho hình chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông cạnh a. Mặt bên hợp với đáy một góc . Tính VS ABCD . theo a và . Bài 6. Tính thể tích khối chóp tứ giác đều S.ABCD có cạnh đáy bằng a và góc ASB = α . Áp dụng: Tính VS ABCD . trong trường hợp α = 60 độ.
Bài 7. Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, góc ABC =120độ . Cho SA vuông góc với đáy và SC = 2a .Tính thể tích hình chóp S.ABCD.
Bài 8. Cho hình chóp S.ABCD có đáy ABCD là một hình thang cân (AB//CD) với AC=20 cm BC=15 cm AB=25 cm . Cho SA vuông góc với đáy và SA =18cm . Tính thể tích của khối chóp.
Bài 9. Cho hình chóp S.ABC có SA vuông góc với đáy. Mặt bên SBC là tam giác đều cạnh a. Cho gócBAC =120 . Tính VS ABC .
. Bài 10. Cho khối chóp S.ABC có đường cao SA bằng a, đáy là tam giác vuông cân có AB= BC= a . Gọi B' là trung điểm của SB, C' là chân đường cao hạ từ A của tam giác S.ABC:
a.Tính thể tích khối chóp S.ABC
b.Chứng minh SC vuông góc với (AB'C')
c.Tính thể tích khối chóp S.ABC
Cho tam giác ABC cân tại A có AD là đường phân giác. Kẻ DE vuông góc với AB tại E, DF vuông góc với AC tại F.
a) Chứng minh: DE=DF
b) Chứng minh tam giác ABD = tam giác ACD.Suy ra AD vuông góc với BC
c) Trường hợp góc A = 80 độ.Hãy so sánh các cạnh của tam giác AED
Mn giúp mk làm nha!
Đây là bài tập hè của mk nhưg mk dốt hình nên mong mn làm cùng mk nha!
a/ \(\Delta ADE\)vuông và \(\Delta ADF\)vuông có:
\(\widehat{EAD}=\widehat{DAF}\)(AD là đường phân giác của \(\Delta ABC\))
Cạnh huyền AD chung
=> \(\Delta ADE\)vuông = \(\Delta ADF\)vuông (cạnh huyền - góc nhọn)
=> DE = DF (hai cạnh tương ứng) (đpcm)
b/ \(\Delta ABD\)và \(\Delta ACD\)có:
AB = AC (\(\Delta ABC\)cân tại A)
\(\widehat{EAD}=\widehat{DAF}\)(AD là đường phân giác của \(\Delta ABC\))
Cạnh AD chung
=> \(\Delta ABD\)= \(\Delta ACD\)(c. g. c)
Ta có AB = AC (\(\Delta ABC\)cân tại A)
=> A thuộc đường trung trực của BC
=> AD \(\perp\)BC (đpcm)
c/ Ta có AD là đường phân giác của \(\Delta ABC\)
=> \(\widehat{DAB}=\frac{\widehat{BAC}}{2}=\frac{80^o}{2}=40^o\)(tính chất tia phân giác)
và \(\widehat{EDA}=90^o-\widehat{DAB}\)(\(\Delta ADB\)vuông tại D)
=> \(\widehat{EDA}=90^o-40^o=50^o\)
Ta lại có: \(\widehat{DAB}< \widehat{EDA}\)(vì 40o < 50o)
=> DE < AE (quan hệ giữa góc và cạnh đối diện trong tam giác)
và \(\hept{\begin{cases}DA< AE\\DA< DE\end{cases}}\)(quan hệ giữa đường vuông góc và đường xiên)
=> DA < DE < AE (đpcm)
Đúng 0
Bình luận (0)
a)Xét tam giác EAD và FAD có
AÊD= góc AFD=90*
AD là cạnh chung
góc EAD=góc FAD(tam giác ABC cân)
=>tam giác ...=...(cạnh huyền-góc nhọn)
=>DE=DF
b)Xét tam giác ABD và ACD có
BA=CA(gt)
BÂD=CÂD(gt)
AD là cạnh chung
=>tam giác ...=...(c-g-c)
=>góc BDA=CDA
mà BDA+CDA=180*
=>BDA=CDA=180*/2=90*
=>AD vuông góc với BC
c) Xét tam giác AED có: AÊD+EÂD+ góc EDA=180*
=>90*+(80*/2)+góc EAD=180*
=>90*+40*+góc EAD=180*
=>góc EAD=180*-(90*+40*)
=>góc EAD=50*
ta có:EÂD<góc ADE<AÊD(40*<50*<90*)
=>ED<AE<AD
Vậy, ED<AE<AD.
Đúng 1
Bình luận (0)
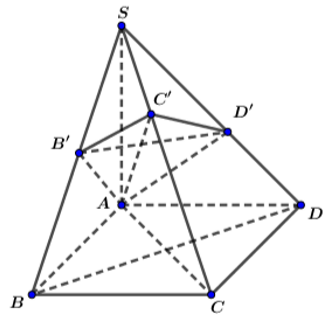
Hình chóp A.ABCD có đáy là hình vuông ABCD cạnh a, cạnh SA bằng a và vuông góc với mặt phẳng (ABCD)
a) Chứng minh rằng các mặt bên kia của hình chóp là những tam giác vuông
b) Mặt phẳng \(\left(\alpha\right)\) đi qua A và vuông góc với cạnh SC lần lượt cắt SB, SC, SD tại B', C', D'. Chứng minh B'D' song song với BD và AB' vuông góc với SB
Em hãy lần lượt tính tham số góc quay của bút vẽ trong trường hợp cần vẽ các hình có số góc là? Giúp mk với ah
Cho hình chóp S.ABCD có SA vuông góc với đáy, đáy ABCD là hình thoi. Mp \(\left(\alpha\right)\) qua A vuông góc với SC tại H cắt SB,SD lần lượt tại E và F. Đường thẳng qua E và F song song với SC cắt BC,CD lần lượt tại M,N. Biết SC hợp với đáy góc 30 độ. Tính diện tích AMCN, biết diện tích AEHF bằng 12
cho góc xoy=40 độ.vẽ tia oz sao cho gocsyoz=30 độ.
a/tia oz có xác định duy nhất ko?
b/tính góc xoz trong từng trường hợp.
GIÚP MK VỚI MK TÍCK CHO 3 CÁI
Bài 1: Một tấm tôn hình vuông cạnh 12dm .Cắt 4 hình vuông con bằng nhau ở 4 góc tấm tôn rồi gò theo nét đứt và gấp lên thành môt cái thùng hình hộp chữ nhật không nắp.Hãy tính thể tích của cái thùng trong các trường hợp sau:a)Cạnh hình vuông bị cắt là 1dmb)Cạnh hình vuông bị cắt là 2dmc) Cạnh hình vuông bị cắt là 3dmBài 2: Cho tam giác ABC vuông có cạnh góc vuông AB40.M là một điểm trên cạnh AC và AM 1/4AC. Từ M kẻ đường vuông gó với AC cắt cạnh BC tại N .Tính độ dài MN
Đọc tiếp
Bài 1: Một tấm tôn hình vuông cạnh 12dm .Cắt 4 hình vuông con bằng nhau ở 4 góc tấm tôn rồi gò theo nét đứt và gấp lên thành môt cái thùng hình hộp chữ nhật không nắp.Hãy tính thể tích của cái thùng trong các trường hợp sau:
a)Cạnh hình vuông bị cắt là 1dm
b)Cạnh hình vuông bị cắt là 2dm
c) Cạnh hình vuông bị cắt là 3dm
Bài 2: Cho tam giác ABC vuông có cạnh góc vuông AB=40.M là một điểm trên cạnh AC và AM =1/4AC. Từ M kẻ đường vuông gó với AC cắt cạnh BC tại N .Tính độ dài MN
Cho hình chữ nhật \(ABCD\). Giải thích tại sao \(ABCD\) là hình vuông trong mỗi trường hợp sau:
Trường hợp 1: \(AB = BC\)
Trường hợp 2: \(AC\) vuông góc với \(BD\)
Trường hợp 3: \(AC\) là đường phân giác của góc \(BAD\)
\(ABCD\) là hình chữ nhật (gt)
Suy ra \(AB = CD\); \(AD = BC\); \(AB\) // \(CD\); \(AD\) // \(BC\) (3)
\(\widehat A = \widehat B = \widehat C = \widehat D = 90^\circ \) (1)
TH1:
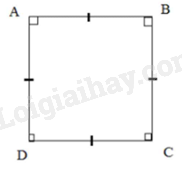
Nếu \(AB = BC\) (gt) thì \(AB = BC = CD = DA\) (2)
Từ (1), (2) suy ra \(ABCD\) là hình vuông
TH2:
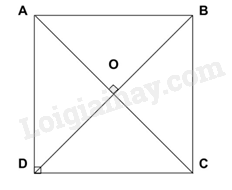
Nếu \(AC\) vuông góc với \(BD\)
Mà \(ABCD\) cũng là hình bình hành
Suy ra \(ABCD\) là hình thoi
Suy ra \(AB = BC = CD = DA\) (4)
Từ (1) và (4) suy ra \(ABCD\) là hình vuông
TH3:
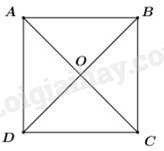
\(AC\) là phân giác của góc \(BAD\)
Mà \(ABCD\) là hình bình hành
Suy ra \(ABCD\) là hình thoi
Suy ra \(AB = BC = CD = DA\) (5)
Từ (1) và (5) suy ra \(ABCD\) là hình vuông
Đúng 0
Bình luận (0)
Bài 1. Cho hình chóp SABCD có cạnh bên SC vuông góc với đáy. Đáy ABCD là hình thoi tâm O, trong đó AABC là tam giác đều có cạnh a. Gọi H là hình chiếu vuông góc của C lên SO. Tính góc giữa SB và (ABCD)
Đề bài thiếu dữ liệu định vị điểm S (ví dụ SC bằng bao nhiêu đó) nên ko thể tính góc giữa SB và (ABCD)
Đúng 0
Bình luận (0)