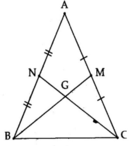
cho tam giác abc có hai đường trung tuyến bm và cn nếu bm=cn thì tam giác abc là tam giác gì
H24
Những câu hỏi liên quan
Cho tam giác ABC có hai đường trung tuyến BM, CN.
a) Chứng minh nếu tam giác ABC cân tại A thì BM = CN.
b) Ngược lại nếu BM = CN, chứng minh:
i) GB = GC, GN = GM;
ii) BN = CM;
iii) tam giác ABC cân tại A.
cho tam giác abc có ab< ac. bm và cn là hai đường trung tuyến của tam giác abc. chứng minh rằng cn> bm
CHo Tam giác ABC có 3 góc nhọn. Đường cao AH, trung tuyến BM, phân giác CN. Gọi P,Q,R là giao điểm của AH và BM; BM và CN; CN và AH. CM nếu P,Q,R tạo thành tam giác thì tam giác đó không đều
Cho tam giác ABC có AB<AC. Biết BM và CN là hai đường trung tuyến của tam giác ABC. CMR: BM<CN
áp dụng t/c đường trung tuyến là xong
Đúng 0
Bình luận (0)
Cho tam giác ABC, các đường trung tuyến BM và CN cắt nhau tại I. Gọi H là trung điểm của IB, K là trung điểm của IC.a) Chứng minh tứ giác MNHK là hình bình hànhb) Nếu các đường trung tuyến BM và CN vuông góc vời nhau thì tứ giác MNHK là hình gì?c) Tam giác ABC có điều kiện gì thì tứ giác MNHK là hình chữ nhật? d) Tam giác ABC có điều kiện gì thì tứ giác MNHK là hình vuông?
Đọc tiếp
Cho tam giác ABC, các đường trung tuyến BM và CN cắt nhau tại I. Gọi H là trung điểm của IB, K là trung điểm của IC.
a) Chứng minh tứ giác MNHK là hình bình hành
b) Nếu các đường trung tuyến BM và CN vuông góc vời nhau thì tứ giác MNHK là hình gì?
c) Tam giác ABC có điều kiện gì thì tứ giác MNHK là hình chữ nhật?
d) Tam giác ABC có điều kiện gì thì tứ giác MNHK là hình vuông?
Cho tam giác ABC có AB < AC . BM và CN là hai đường trung tuyến của tam giác ABC . Chứng minh rằng CN > BM
Cho tam giác ABC có 2 đường trung tuyến BM, CN cắt nahu tại điểm G.
a, C/m nếu tam giác ABC cân tại A thì BM = CN.
b, Ngược lại nếu BM = CN , c/m:
i,GB = GC, GN = GM;
ii, BN = CM
iii, Tam giác ABC cân tại A
Cho tam giác ABC, có hai đường trung tuyến BM, CN. Chứng minh tam giác ANC = tam giác AMB. Chứng minh CN = BM
Sửa đề: ΔABC cân tại A
AB=AC
=>1/2AB=1/2AC
=>AN=AM
Xét ΔANC và ΔAMB có
AN=AM
góc NAC chung
AC=AB
=>ΔANC=ΔAMB
=>CN=BM
Đúng 0
Bình luận (0)
Cho tam giác ABC có trung tuyến BM, CN cắt tại I, H là trung điểm của IB, K là trung điểm của IC
a/Chứng minh MNHK là hình bình hành
b/Nếu BM vuông góc với CN thì MNHK là hình gì?
c/Tam giác ABC có điều kiện gì thì MNHK là hình chữ nhật?
d/Tam giác ABC có điều kiện gì thì MNHK là hình vuông?
Bạn tự vẽ hình nhé
a) Ta có: \(IN=\frac{1}{3}NC\)và
\(IC=\frac{2}{3}NC\Leftrightarrow IK=\frac{IC}{2}=\frac{2}{3}NC\cdot\frac{1}{2}=\frac{1}{3}NC\)
\(\Rightarrow IN=IK\)(1)
Mặt khác \(IM=\frac{1}{3}BM\)và
\(IB=\frac{2}{3}BM\Leftrightarrow HI=\frac{IB}{2}=\frac{2}{3}BM\cdot\frac{1}{2}=\frac{1}{3}BM\)
\(\Rightarrow IM=IH\)(2)
Từ (1) và (2) => tứ giác MNHK là hbh. (3)
b) Từ (3) => Nếu BM_|_ CN thì tứ giác MNHK là hình thoi (4)
c) Để MNHK là hcn thì NK = HM hay IN = IM <=> NC=BM <=> tam giác ABC cân tại A
d) Từ (4) và c) => Để MNHK là hình vuông thì tam giác ABC cân tại A và BM _|_ CN
Đúng 0
Bình luận (0)