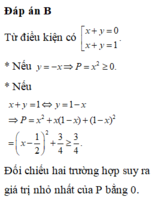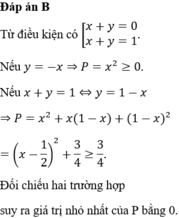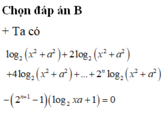Tìm các giá trị nguyên x,y thoả mãn đẳng thức (y+2)x2+1=y2
LK
Những câu hỏi liên quan
Tìm các giá trị nguyên x,y thoả mãn đẳng thức \(\left(y+2\right)x^2+1=y^2\)
\(\left(y+2\right)x^2+1=y^2\Leftrightarrow x^2y+2x^2+1-y^2=0\Leftrightarrow\)\(x^2y+2x^2+4-y^2-3=0\Leftrightarrow x^2\left(y+2\right)-\left(y^2-4\right)=3\)\(\Leftrightarrow x^2\left(y+2\right)-\left(y+2\right)\left(y-2\right)=3\)
\(\Leftrightarrow\left(y+2\right)\left(x^2-y+2\right)=3\)
Ta có bảng:
| y + 2 | 1 | 3 | -1 | -3 |
| x2 - y + 2 | 3 | 1 | -3 | -1 |
| y | -1 | 1 | -3 | -5 |
| x | 0 | 0 | Không tồn tại | Không tồn tại |
| KL | Chọn | Chọn |
Vậy ta tìm được cặp (x ; y) = (0 ; 1) và (0; -1).
Đúng 0
Bình luận (0)
\(PT\Leftrightarrow x^2\left(y+2\right)+4-y^2=3\)
\(\Leftrightarrow\left(y+2\right)\left(x^2+2-x\right)=3\)
+, Trường hợp: \(\hept{\begin{cases}y+2=3\\x^2+2-x=1\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x=0\\y=1\end{cases}}\)
+, Trường hợp: \(\hept{\begin{cases}y+2=1\\x^2+2-x=3\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}x=0\\y=-1\end{cases}}\)
Đúng 0
Bình luận (0)
Cho các số thực x,y thoả mãn x+y 2.Tìm giá trị nhỏ nhất của biểu thức: A x3�3 + y3�3 + x2�2 + y2
Đọc tiếp
Cho các số thực x,y thoả mãn x+y =2.Tìm giá trị nhỏ nhất của biểu thức: A= + + +
Lời giải:
$A=(x+y)(x^2-xy+y^2)+x^2+y^2=2(x^2-xy+y^2)+x^2+y^2=2(x^2+y^2)+(x-y)^2$
$\geq 2(x^2+y^2)=(1^2+1^2)(x^2+y^2)\geq (x+y)^2=2^2=4$ (theo BĐT Bunhiacopxky)
Vậy $A_{\min}=4$. Giá trị này đạt tại $x=y=1$
Đúng 0
Bình luận (0)
Cho các số thực x, y thoả mãn x2+y2=5 Tìm Giá Trị Lớn Nhất Của Biểu Thức P= x+2y
\(P-\dfrac{5}{2}=x+2y-\dfrac{x^2+y^2}{2}=-\dfrac{1}{2}\left(x-1\right)^2-\dfrac{1}{2}\left(y-2\right)^2+\dfrac{5}{2}\le\dfrac{5}{2}\)
\(\Rightarrow P-\dfrac{5}{2}\le\dfrac{5}{2}\Rightarrow P\le5\)
\(P_{max}=5\) khi \(\left(x;y\right)=\left(1;2\right)\)
Đúng 1
Bình luận (1)
Cho các số thực x, y thoả mãn
2
x
+
y
-
1
(
3
x
+
y
+
1
)
3
x
+
3
y
+
1
. Giá trị nhỏ nhất của biểu thức
P
x...
Đọc tiếp
Cho các số thực x, y thoả mãn 2 x + y - 1 ( 3 x + y + 1 ) = 3 x + 3 y + 1 . Giá trị nhỏ nhất của biểu thức P = x 2 + x y + y 2 bằng
A. 3 4
B. 0
C. 1 4
D. 1 2
Cho các số thực x, y thoả mãn
2
x
+
y
-
1
(
3
x
+
y
+
1
)
3
x
+
3
y
+
1
. Giá trị nhỏ nhất của biểu thức P
x
2
+
x
y...
Đọc tiếp
Cho các số thực x, y thoả mãn 2 x + y - 1 ( 3 x + y + 1 ) = 3 x + 3 y + 1 . Giá trị nhỏ nhất của biểu thức P= x 2 + x y + y 2 bằng
A. 3 4
B. 0.
C. 1 4
D. 1 2
Cho hàm số
y
ln
(
2
x
-
a
)
-
2
m
ln
(
2
x
-
a
)
+...
Đọc tiếp
Cho hàm số y = ln ( 2 x - a ) - 2 m ln ( 2 x - a ) + 2 (m là tham số thực), trong đó x, a là các số thực thỏa mãn đẳng thức
log 2 ( x 2 + a 2 ) + log 2 ( x 2 + a 2 ) + log 2 ( x 2 + a 2 ) + . . . + log . . . 2 ( x 2 + a 2 ) - ( 2 n + 1 - 1 ) ( log 2 x a + 1 ) = 0
(với n là số nguyên dương). Gọi S là tập hợp các giá trị của m thoả mãn m a x [ 1 ; e 2 ] y = 1 . Số phần tử của S là
A. 0
B. 1
C. 2
D. Vô số
cho hai số thực x>0,y>0 thoả mãn xy=6.Tìm giá trị nhỏ nhất của biểu thức P=x2+y2
Áp dụng BĐT cói cho 2 số ko âm ta có
X^2+y^2 >= 2 .căn x^2 .y^2 = 2.xy= 2.6 =12
Vậy P min =12 dấu = xảy ra khi x^2=y^2 <=> x=y
( thông cảm mình gõ mũ ko đc )
Đúng 1
Bình luận (0)
Giả sử x, y là các số dương thoả mãn đẳng thức: x + y = căn bậc 2 của 10
Tìm giá trị của x và y để biểu thức: P = (x4 + 1)(y4 + 1) đạt giá trị nhỏ nhất. Tìm giá trị nhỏ nhất ấy.
P = x4.y4 + x4 + y4 + 1
Ta có: x2 + y2 = (x + y)2 - 2xy = 10 - 2xy => x4 + y4 = (x2 + y2)2 - 2x2y2 = (10 - 2xy)2 - 2(xy)2 = 100 - 40xy + 2(xy)2
=> P = (xy)4 + 2(xy)2 - 40xy + 101 = [(xy)4 - 8(xy)2 + 16] + 10.[(xy)2 - 4xy + 4] + 45 = [(xy)2 - 4]2 + 10.(xy - 2)2 + 45
=> P > 45
Dấu "=" xảy ra <=> xy = 2
Mà có x + y = \(\sqrt{10}\) => x = \(\sqrt{10}\) - y => xy = \(\sqrt{10}\)y - y2 = 2 => y2 - \(\sqrt{10}\).y + 2 = 0
\(\Delta\) = 10 - 8 = 2 => \(y=\frac{\sqrt{10}+\sqrt{2}}{2}\)=> x = \(\frac{4}{\sqrt{10}+\sqrt{2}}=\frac{\sqrt{10}-\sqrt{2}}{2}\)
vậy P nhỏ nhất bằng 45 khi x = \(\frac{\sqrt{10}-\sqrt{2}}{2}\); \(y=\frac{\sqrt{10}+\sqrt{2}}{2}\)
Đúng 0
Bình luận (0)
hok giỏi nhưng cx có bài bế tắc chứ bộ đâu fai hok giỏi nhất thiết là cái gì cx biết đâu
Đúng 0
Bình luận (0)
 Miki Thảo ơi,mk đồng ý zới ý kiến của bn!
Miki Thảo ơi,mk đồng ý zới ý kiến của bn!
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Giả sử x, y là các số dương thoả mãn đẳng thức: x + y = căn bậc 2 của 10
Tìm giá trị của x và y để biểu thức: P = (x4 + 1)(y4 + 1) đạt giá trị nhỏ nhất. Tìm giá trị nhỏ nhất ấy.
P = x4.y4 + x4 + y4 + 1
Ta có: x2 + y2 = (x + y)2 - 2xy = 10 - 2xy => x4 + y4 = (x2 + y2)2 - 2x2y2 = (10 - 2xy)2 - 2(xy)2 = 100 - 40xy + 2(xy)2
=> P = (xy)4 + 2(xy)2 - 40xy + 101 = [(xy)4 - 8(xy)2 + 16] + 10.[(xy)2 - 4xy + 4] + 45 = [(xy)2 - 4]2 + 10.(xy - 2)2 + 45
=> P > 45
Dấu "=" xảy ra <=> xy = 2
Mà có x + y = \(\sqrt{10}\) => x = \(\sqrt{10}\) - y => xy = \(\sqrt{10}\)y - y2 = 2 => y2 - \(\sqrt{10}\).y + 2 = 0
\(\Delta\) = 10 - 8 = 2 => \(y=\frac{\sqrt{10}+\sqrt{2}}{2}\)=> x = \(\frac{4}{\sqrt{10}+\sqrt{2}}=\frac{\sqrt{10}-\sqrt{2}}{2}\)
vậy P nhỏ nhất bằng 45 khi x = \(\frac{\sqrt{10}-\sqrt{2}}{2}\); \(y=\frac{\sqrt{10}+\sqrt{2}}{2}\)
Đúng 0
Bình luận (0)