Cho x,y là hai số tự nhiên khác 0.Tìm giá trị nhỏ nhất của biểu thức A= |36x-5y|
CT
Những câu hỏi liên quan
A= |36x−5y||36x−5y| với x,y là các số tự nhiên khác 0. Tìm GTNN của biểu thức A.
A= |36x−5y| với x,y là các số tự nhiên khác 0. Tìm GTNN của biểu thức A.
cho x,y là các số tự nhiên khác 0, tìm giá trị nhỏ nhất của biểu thức A=|36x-5y|
cho x,y là các số tự nhiên khác 0, tìm giá trị nhỏ nhất của biểu thức: A= | 36x-5y|
Cho x,y là các số tự nhiên khác 0 , tìm giá trị nhỏ nhất của biểu thức :
\(A=\left|36^x-5^y\right|\)
vào link này bn
https://i.imgur.com/6JibVkl.png
Tìm số tự nhiên nhỏ nhất khác 0 mà khi nhân nó với 135 ta được một số chính phương:
Giá trị của x và y để biểu thức A= |x + 15| +|-25-y| - 79 đạt giá trị nhỏ nhất là ?
dễ thì làm đi nguyenmanhtrung
Đúng 0
Bình luận (0)
Cho x;y;z>0 ;x+y+z=1
tìm giá trị nhỏ nhất của biểu thức
P=\(\frac{15x^2}{z}+\frac{5y^2}{36x}+\frac{24z^2}{25y}\)
a, cho x, y là 2 số thoả mãn (2x - y + 7)^{2022} + |x - 1|^{2023} ≤ 0. Tính giá trị của biểu thức: P x^{2023} + (y - 10)^{2023}b, Tìm số tự nhiên x, y biết 25 - y^2 8(x 2023)^2 c, Tìm giá trị nhỏ nhất của biểu thức: P (|x - 3| + 2)^2 + |y + 3| + 2019d, Tìm cặp số nguyên x, y biết: (2 - x)(x + 1) |y + 1|
Đọc tiếp
a, cho x, y là 2 số thoả mãn (2x - y + 7)\(^{2022}\) + |x - 1|\(^{2023}\) ≤ 0. Tính giá trị của biểu thức: P = x\(^{2023}\) + (y - 10)\(^{2023}\)
b, Tìm số tự nhiên x, y biết 25 - y\(^2\) = 8(x = 2023)\(^2\)
c, Tìm giá trị nhỏ nhất của biểu thức: P = (|x - 3| + 2)\(^2\) + |y + 3| + 2019
d, Tìm cặp số nguyên x, y biết: (2 - x)(x + 1) = |y + 1|
a: \(\left(2x-y+7\right)^{2022}>=0\forall x,y\)
\(\left|x-1\right|^{2023}>=0\forall x\)
=>\(\left(2x-y+7\right)^{2022}+\left|x-1\right|^{2023}>=0\forall x,y\)
mà \(\left(2x-y+7\right)^{2022}+\left|x-1\right|^{2023}< =0\forall x,y\)
nên \(\left(2x-y+7\right)^{2022}+\left|x-1\right|^{2023}=0\)
=>\(\left\{{}\begin{matrix}2x-y+7=0\\x-1=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=2x+7=9\end{matrix}\right.\)
\(P=x^{2023}+\left(y-10\right)^{2023}\)
\(=1^{2023}+\left(9-10\right)^{2023}\)
=1-1
=0
c: \(\left|x-3\right|>=0\forall x\)
=>\(\left|x-3\right|+2>=2\forall x\)
=>\(\left(\left|x-3\right|+2\right)^2>=4\forall x\)
mà \(\left|y+3\right|>=0\forall y\)
nên \(\left(\left|x-3\right|+2\right)^2+\left|y+3\right|>=4\forall x,y\)
=>\(P=\left(\left|x-3\right|+2\right)^2+\left|y-3\right|+2019>=4+2019=2023\forall x,y\)
Dấu '=' xảy ra khi x-3=0 và y-3=0
=>x=3 và y=3
Đúng 0
Bình luận (0)
Cho x, y là hai số thực khác 0. Tìm giá trị nhỏ nhất của biểu thức: M
4
x
2
y
2
x
2
+
y
2...
Đọc tiếp
Cho x, y là hai số thực khác 0. Tìm giá trị nhỏ nhất của biểu thức: M = 4 x 2 y 2 x 2 + y 2 + x 2 y 2 + y 2 x 2
Biến đổi M, ta được
M = 4 x 2 y 2 x 2 + y 2 + x 2 y 2 + y 2 x 2 = 4 x y + y x 2 + x y 2 + y x 2
Đặt a = x y ; b = y x ta được ab = 1, suy ra a 2 + b 2 ≥ 2
Từ đó ta có
M = 4 a + b 2 + a 2 + b 2 = 4 a 2 + b 2 + 2 + a 2 + b 2 + 2 4 + 3 a 2 + b 2 + 2 4 - 2 ≥ 2 + 3 – 2 = 3
Dấu "=" xảy ra <=> a = b = ±1 <=> 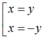
Đúng 0
Bình luận (0)



