a) Xét tam thức \(f\left( x \right) = 7{x^2} - 19x - 6\) có \(\Delta  = 529 > 0\), có hai nghiệm phân biệt \({x_1} =  - \frac{2}{7},{x_2} = 3\) và có \(a = 7 > 0\)

Ta có bảng xét dấu như sau

Vậy nghiệm của bất phương trình là đoạn \(\left[ { - \frac{2}{7};3} \right]\)

b) \( - 6{x^2} + 11x > 10 \Leftrightarrow  - 6{x^2} + 11x - 10 > 0\)

Xét tam thức \(f\left( x \right) =  - 6{x^2} + 11x - 10\) có \(\Delta  =  - 119 < 0\)và có \(a =  - 6 < 0\)

Ta có bảng xét dấu như sau

Vậy bất phương trình vô nghiệm

c) \(3{x^2} - 4x + 7 > {x^2} + 2x + 1 \Leftrightarrow 2{x^2} - 6x + 6 > 0\)

Xét tam thức \(f\left( x \right) = 2{x^2} - 6x + 6\) có \(\Delta  =  - 12 < 0\)và có \(a = 2 > 0\)

Ta có bảng xét dấu như sau

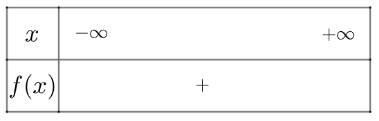
Vậy bất phương trình có vô số nghiệm

d) Xét tam thức \(f\left( x \right) = {x^2} - 10x + 25\) có \(\Delta  = 0\), có nghiệm kép \({x_1} = {x_2} = 5\) và có \(a = 1 > 0\)

Ta có bảng xét dấu như sau

Vậy nghiệm của bất phương trình là \(x = 5\)

...

<=> 3x^5(x-3) - 4x^4(x-3) + 7x^3(x-3) - 5x^2(x-3) + 4x(x-3) - (x-3) = 0 

<=> (x-3)(3x^5 - 4x^4 + 7x^3 - 5x^2 + 4x - 1) = 0 

<=> (x-3)[3x^4(x-1/3) - 3x^3(x-1/3) + 6x^2(x-1/3) - 3x(x-1/3) + 3(x-1/3)] = 0 

<=> (x-3)(x-1/3)(3x^4 - 3x^3 + 6x^2 - 3x + 3) = 0 

<=> (x-3)(x-1/3)[3(x^4+2x^2+1) - 3x(x^2+1)] = 0 

<=> (x-3)(x-1/3)(x^2+1)[3(x^2+1) - 3x]  = 0 

<=> 3(x-3)(x-1/3)(x^2+1)(x^2+1-x) = 0 

.... 

a, 5x - 7(3 - x) = 3

=> 5x - 21 + 7x = 3

=> 12x = 24

=> x = 2

b, 4x² + 3x = 0

=> x(4x + 3) = 0 

=> \(\orbr{\begin{cases}x=0\\4x+3=0\end{cases}}\)

=> \(\orbr{\begin{cases}x=0\\x=\frac{-3}{4}\end{cases}}\)

c, (x + 1)² - 4x² =0

=> (x + 1)² - (2x)² = 0

=> (x + 1 - 2x)(x + 1 + 2x) = 0

=> (1 - x)(3x+ 1) = 0

=> \(\orbr{\begin{cases}1-x=0\\3x+1=0\end{cases}}\)

=> \(\orbr{\begin{cases}x=1\\x=\frac{-1}{3}\end{cases}}\)

d, x³ - 19x - 30 = 0

=> x³ - 5x² + 5x² - 25x + 6x - 30 = 0

=> x²(x - 5) + 5x(x - 5) + 6(x - 5) = 0

=> (x² + 5x + 6)(x - 5) = 0

=> (x² + 2x + 3x + 6)(x - 5) = 0

=> (x + 2)(x + 3)(x - 5) = 0

=> x + 2 = 0 hoặc x + 3 = 0 hoặc x - 5 = 0

=> x = -2 hoặc x = -3 hoặc x = 5

=> x thuộc {-2; -3; 5}

a, x=2

b, x=0

c, x=1

d, x=2

kb nha

Tìm x, biết 

a) 5x-7(3-x)=3 nghi đề sai

b) 4x²+3x=0 \(\Leftrightarrow x\left(4x+3\right)=0=>\orbr{\begin{cases}x=0\\x=-\frac{3}{4}\end{cases}}\)

c) (x+1)²-4x²=0\(\Leftrightarrow\left(x+1\right)^2-\left(2x\right)^2\Leftrightarrow\orbr{\begin{cases}x+1-2x=0\Rightarrow x=1\\x+1+2x=0\Rightarrow x=-\frac{1}{3}\end{cases}}\)

d) x³-19x-30=0 nghi đe sai lớp 8 khó thế

= 7/19 . (1/3 + 2/3)

= 7/19 . 3/3

= 7/19 . 1

= 7/19

= 7/19 . (1/3 + 2/3)

= 7/19 . 3/3

= 7/19 . 1

= 7/19

\(x^2-19x-56=0\)

\(\Leftrightarrow x^2-19x=56\)

\(\Leftrightarrow x^2-19x+\frac{361}{4}=56+\frac{361}{4}\)

\(\Leftrightarrow x^2-2.x.\frac{19}{2}+\left(\frac{19}{2}\right)^2=\frac{585}{4}\)

\(\Leftrightarrow\left(x-\frac{19}{2}\right)^2=\frac{585}{4}\)

\(\Leftrightarrow\left(x-\frac{19}{2}\right)^2=\left(\pm\sqrt{\frac{585}{4}}\right)^2\)

\(\Leftrightarrow\left[{}\begin{matrix}x-\frac{19}{2}=\sqrt{\frac{585}{4}}\\x-\frac{19}{2}=-\sqrt{\frac{585}{4}}\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x-\frac{19}{2}=\frac{\sqrt{585}}{2}\\x-\frac{19}{2}=-\frac{\sqrt{585}}{2}\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=\frac{\sqrt{585}+19}{2}\\x=\frac{-\sqrt{585}+19}{2}\end{matrix}\right.\)

\(\Leftrightarrow x^3-x^2-8x^2+8x+11x-11=0\)

\(\Leftrightarrow x^2\left(x-1\right)-8x\left(x-1\right)+11\left(x-1\right)=0\)

\(\Leftrightarrow\left(x-1\right)\left(x^2-8x+11\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x-1=0\\x^2-8x+11=0\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=4-\sqrt{5}\\x=4+\sqrt{5}\end{matrix}\right.\)