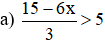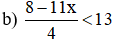giải bất phương trình 3x - 4x + 6
NN
Những câu hỏi liên quan
Bài 1: Giải phương trình và bất phương trình sau: 1. 5.(2-3x). (x-2) = 3.( 1-3x) 2. 4x^2 + 4x + 1= 0 3. 4x^2 - 9= 0 4. 5x^2 - 10=0 5. x^2 - 3x= -2 6. |x-5| - 3= 0
Bài 1: Giải các bất phương trình và phương trình sau :
a) 2(3-4x) = 10-(2x – 5)
Giải các bất phương trình và phương trình sau :
a) 3(2-4x) = 11-(3x – 1)
Bài 1:
a) Ta có: \(2\left(3-4x\right)=10-\left(2x-5\right)\)
\(\Leftrightarrow6-8x-10+2x-5=0\)
\(\Leftrightarrow-6x+11=0\)
\(\Leftrightarrow-6x=-11\)
hay \(x=\dfrac{11}{6}\)
b) Ta có: \(3\left(2-4x\right)=11-\left(3x-1\right)\)
\(\Leftrightarrow6-12x-11+3x-1=0\)
\(\Leftrightarrow-9x-6=0\)
\(\Leftrightarrow-9x=6\)
hay \(x=-\dfrac{2}{3}\)
Đúng 2
Bình luận (0)
Giải các bất phương trình:
A) 2/3x > -6 B) -5/6x < 20
C) 3 - 1/4x > 2
Xem chi tiết
\(a,bpt\Leftrightarrow2x>-18\Leftrightarrow x>-9\)
\(b,bpt\Leftrightarrow-5x< 120\Leftrightarrow x>-24\)
\(c,bpt\Leftrightarrow-x>-4\Leftrightarrow x< 4\)
Giải hôi túi với ạ
Bàil: Giải phương trình sau a) 2x - 3 3 - x b) 7x - 4 3x + 12 c) 3x - 6 + x 9 - x d) 10x - 12 - 3x 6 + x Bài 2: Giải bất phương trình sau và biểu diễn tập nghiệm trên trục số: a) 4x + 6 2x - 2 b) 3x + 15 0 c) 3x - 3 x + 5 d) x - 4 - 2x + 5 Bài3: a) Một người đi xe máy từ 4 đến B với vận tốc 25km/h. Lúc về người đó đi với vận tốc 30km/h, nên thời gian về ít hơn thời gian đi là 20 phút. Tính AB ? b) Một người đi xe đạp từ A đến B với vận tốc 15 km/h. Sau đó quay về từ B về A với vận tốc 12...
Đọc tiếp
Bàil: Giải phương trình sau a) 2x - 3 = 3 - x b) 7x - 4 = 3x + 12 c) 3x - 6 + x = 9 - x d) 10x - 12 - 3x = 6 + x Bài 2: Giải bất phương trình sau và biểu diễn tập nghiệm trên trục số: a) 4x + 6 <= 2x - 2 b) 3x + 15 < 0 c) 3x - 3 > x + 5 d) x - 4 > - 2x + 5 Bài3: a) Một người đi xe máy từ 4 đến B với vận tốc 25km/h. Lúc về người đó đi với vận tốc 30km/h, nên thời gian về ít hơn thời gian đi là 20 phút. Tính AB ? b) Một người đi xe đạp từ A đến B với vận tốc 15 km/h. Sau đó quay về từ B về A với vận tốc 12 km/h. Cả đi lẫn về hết 4 giờ 30 phút. Tính quãng đường 4B Bài 4: Cho tam giác ABC vuông tại A với AB = 3cm AC= 4cm vẽ đường cao AE. a) Chứng minh rằng AABC đồng dạng với AEBA. b) Tia phân giác của góc ABC cắt AC tại F. Tính BF Bài 5: Cho tam giác ABC có AC = 8cm, AC = 16cm Gọi D và E là hai điểm lần lượt trên cạnh AB và AC sao cho BD = 2cm CE = 13cm Chứng minh rằng a. AAEB AADC b. AED= ABC, cho DE = 5cm Tính BC? C. AE AC AD AB
1:
a: =>3x=6
=>x=2
b: =>4x=16
=>x=4
c: =>4x-6=9-x
=>5x=15
=>x=3
d: =>7x-12=x+6
=>6x=18
=>x=3
2:
a: =>2x<=-8
=>x<=-4
b: =>x+5<0
=>x<-5
c: =>2x>8
=>x>4
Đúng 0
Bình luận (0)
giải bất phương trình sau
a, 3x+5 ≤ 4x-9
b, 6 -2x < 6-x
c, 7 (x-1) +5>-3x
d, -(8x+2) ≤ 7 (1-x)
a: Ta có: \(3x+5\le4x-9\)
\(\Leftrightarrow-x\le-14\)
\(\Leftrightarrow x\ge14\)
b: Ta có: \(6-2x< 6-x\)
\(\Leftrightarrow-x< 0\)
hay x>0
c: Ta có: \(7\left(x-1\right)+5>-3x\)
\(\Leftrightarrow7x-7+5+3x>0\)
\(\Leftrightarrow10x>2\)
hay \(x>\dfrac{1}{5}\)
Đúng 0
Bình luận (0)
giải bất phương trình
1)2x+3<0
2)3x-8>4x-12
3)3x-2>4x+3
Giải bất phương trình | 4x | = 3x + 1
Ta có | 4x | = 3x + 1
+ Với x ≥ 0 ta có | 4x | = 4x
Khi đó phương trình trở thành 4x = 3x + 1
⇔ 4x - 3x = 1 ⇔ x = 1.
Giá trị x = 1 thỏa mãn điều kiện x ≥ 0, nên 1 là một nghiệm của phương trình đã cho
+ Với x < 0 ta có | 4x | = - 4x
Khi đó phương trình trở thành - 4x = 3x + 1
⇔ - 4x - 3x = 1 ⇔ - 7x = 1 ⇔ x = - 1/7.
Giá trị x = - 1/7 thỏa mãn điều kiện x < 0, nên - 1/7 là một nghiệm cần tìm.
Vậy phương trình đã cho có tập nghiệm là S = { - 1/7;1 }
Đúng 0
Bình luận (0)
câu 1 giải bất phương trình
c) 8x + 3(x + 1) > 5x - (2x - 6)
d) 2x(6x – 1) > (3x – 2)(4x + 3)
a) \(\dfrac{15-6x}{3}>5\Leftrightarrow15-6x>15\)
\(\Leftrightarrow-6x>0\Leftrightarrow x< 0\) (vì \(-6< 0\))
\(S=\left\{x|x< 0\right\}\)
b) \(\dfrac{8-11x}{4}< 13\Leftrightarrow8-11x< 52\)
\(\Leftrightarrow-11x< -44\Leftrightarrow x>4\) (vì \(-11< 0\))
\(S=\left\{x|x>4\right\}\)
c) \(8x+3\left(x+1\right)>5x-\left(2x-6\right)\)
\(\Leftrightarrow8x+3x+1>5x-2x+6\)
\(\Leftrightarrow8x+3x-5x+2x>6-1\)
\(\Leftrightarrow8x>5\)
\(\Leftrightarrow x>\dfrac{5}{8}\) (vì \(8>0\))
\(S=\left\{x|x>\dfrac{5}{8}\right\}\)
d) \(2x\left(6x-1\right)>\left(3x-2\right)\left(4x+3\right)\)
\(\Leftrightarrow12x^2-2x>12x^2+9x-8x-6\)
\(\Leftrightarrow12x^2-2x-12x^2-9x+8x>-6\)
\(\Leftrightarrow-3x>-6\)
\(\Leftrightarrow x< 2\) (vì \(-3< 0\))
\(S=\left\{x|x< 2\right\}\)
Đúng 0
Bình luận (0)
a) \(\dfrac{15-6x}{3}>5\) <=> \(15-6x>15\) <=> \(6x< 0\) <=> \(x< 0\)
b) \(\dfrac{8-11x}{4}< 13\) <=> \(8-11x< 52\) <=> \(11x>-44\)<=> \(x>-4\)
c) \(8x+3\left(x+1\right)>5x-\left(2x-6\right)\)
<=> 8x + 3x + 3 - 5x + 2x - 6 > 0
<=> 8x > 3
<=> x > 3/8
d) 2x(6x - 1) > (3x - 2)(4x + 3)
<=> 12x2 - 2x > 12x2 + x - 6
<=> 12x2 - 2x - 12x2 - x > -6
<=> -3x > -6
<=> x < 2
Đúng 0
Bình luận (0)
Giải bất phương trình sau: 3x^3-4x-1>=0
\(\Leftrightarrow3x^3-3x+x-1\ge0\\ \Leftrightarrow3x\left(x-1\right)\left(x+1\right)+\left(x-1\right)\ge0\\ \Leftrightarrow\left(x-1\right)\left(3x^2+3x+1\right)\ge0\\ \Leftrightarrow x-1\ge0\left(3x^2+3x+1=3\left(x+\dfrac{1}{2}\right)^2+\dfrac{1}{4}>0\right)\\ \Leftrightarrow x\ge1\)
Đúng 1
Bình luận (1)