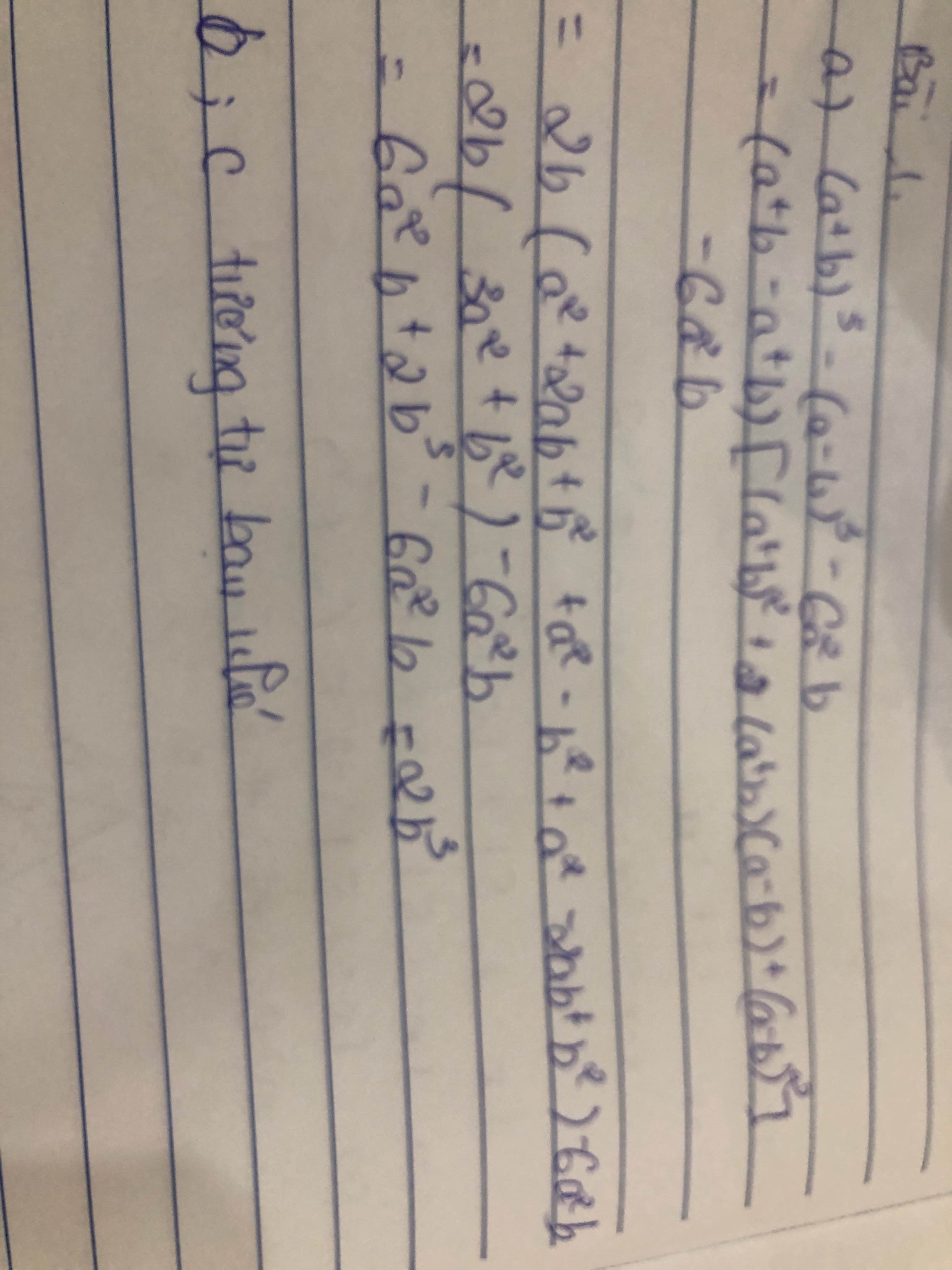rút gọn bt:a)|a|+a / b)|a|-a /c)3(x-1)-2(x-3)
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
TA
Những câu hỏi liên quan
1.cho bt:A=\(\frac{x^3}{x^2-4}-\frac{x}{x-2}-\frac{2}{x+2}\)
a) Rút gọn A
b)Tìm x để A>0,A<0
c)Tìm X để /A/=5
ĐK : \(x\ne2\); \(x\ne-2\)
a) \(A=\frac{x^3}{x^2-4}-\frac{x}{x-2}-\frac{2}{x+2}=\frac{x^3}{\left(x-2\right)\left(x+2\right)}-\frac{x}{x-2}-\frac{2}{x+2}\)
\(=\frac{x^3-x.\left(x+2\right)-2.\left(x-2\right)}{\left(x+2\right).\left(x-2\right)}=\frac{x^3-x^2-2x-2x+4}{\left(x+2\right).\left(x-2\right)}=\frac{x^3-x^2-4x+4}{\left(x+2\right)\left(x-2\right)}\)
\(=\frac{x^2.\left(x-1\right)-4.\left(x-1\right)}{\left(x+2\right)\left(x-2\right)}=\frac{\left(x-1\right).\left(x^2-4\right)}{\left(x+2\right)\left(x-2\right)}=\frac{\left(x-1\right)\left(x+2\right)\left(x-2\right)}{\left(x+2\right)\left(x-2\right)}=x-1\)
b) - Để A > 0 thì x - 1 > 0 => x > 1
- Để A < 0 thì x - 1 < 0 => x < 1
c) Để | A | = 5 thì | x-1 | = 5
+ Nếu \(x-1\ge0\) thì \(x\ge1\) , ta có phương trình
x - 1 = 5 => x = 6 ( thỏa mãn )
+ Nếu x - 1 < 0 thì x < 1 , ta có phương trình :
-x + 1 = 5 < = > -x = 4 <=> x = -4 ( thỏa mãn )
Vậy tập nghiệm của phương trình là S = { -4 ; 6 }
Đúng 0
Bình luận (0)
rút gọn bt:
a,(x+y)^2+(x-y)^2
b,(a-b^2)(a+b^2)
a) `(x+y)^2+(x-y)^2=x^2+2xy+y^2+x^2-2xy+y^2=2x^2+2y^2`
b) `(a-b^2)(a+b^2)=a^2-(b^2)^2=a^2-b^4`
Đúng 1
Bình luận (0)
1 Cho bt:A=\((\frac{1}{x-\sqrt{x}}+\frac{1}{\sqrt{x}-1}):\frac{\sqrt{x}+1}{x-2\sqrt{x}+1}\)
Rút gọn A
Tìm x để A>-1
ĐK: \(x>0;x\ne1\)
\(A=\left(\frac{1}{x-\sqrt{x}}+\frac{1}{\sqrt{x}-1}\right):\frac{\sqrt{x}+1}{x-2\sqrt{x}+1}\)
\(=\left(\frac{1}{\sqrt{x}\left(\sqrt{x}-1\right)}+\frac{\sqrt{x}}{\sqrt{x}\left(\sqrt{x}-1\right)}\right):\frac{\sqrt{x}+1}{\left(\sqrt{x}-1\right)^2}\)
\(=\frac{\sqrt{x}+1}{\sqrt{x}\left(\sqrt{x}-1\right)}.\frac{\left(\sqrt{x}-1\right)^2}{\sqrt{x}+1}\)
\(=\frac{\sqrt{x}-1}{\sqrt{x}}\)
\(A>-1\) \(\Rightarrow\)\(\frac{\sqrt{x}-1}{\sqrt{x}}>-1\)
\(\Leftrightarrow\)\(\frac{\sqrt{x}-1}{\sqrt{x}}+1>0\) \(\Leftrightarrow\)\(\frac{2\sqrt{x}-1}{\sqrt{x}}>0\)
Do \(\sqrt{x}>0\) \(\Rightarrow\)\(2\sqrt{x}-1>0\)\(\Leftrightarrow\)\(2\sqrt{x}>1\)\(\Leftrightarrow\)\(\sqrt{x}>\frac{1}{2}\)\(\Leftrightarrow\)\(x>\frac{1}{4}\)
Vậy \(x>\frac{1}{4}\)\(\left(x\ne1\right)\)thì A > - 1
Đúng 0
Bình luận (0)
\(ĐKXĐ:\hept{\begin{cases}x\ne0\\x\ne1\end{cases}}\)
Ta có: \(A=\left(\frac{1}{x-\sqrt{x}}+\frac{1}{\sqrt{x}-1}\right):\frac{\sqrt{x}+1}{x-2\sqrt{x}+1}\)\(=\left[\frac{1}{\sqrt{x}\left(\sqrt{x}-1\right)}+\frac{1}{\sqrt{x}-1}\right]:\frac{\sqrt{x}+1}{\left(\sqrt{x}\right)^2-2\sqrt{x}+1}\)
\(=\left[\frac{1}{\sqrt{x}\left(\sqrt{x}-1\right)}+\frac{\sqrt{x}}{\sqrt{x}\left(\sqrt{x}-1\right)}\right]:\frac{\sqrt{x}+1}{\left(\sqrt{x}-1\right)^2}\)
\(=\frac{\sqrt{x}+1}{\sqrt{x}\left(\sqrt{x}-1\right)}.\frac{\left(\sqrt{x}-1\right)^2}{\sqrt{x}+1}=\frac{\sqrt{x}-1}{\sqrt{x}}\)
Để \(A>-1\)thì \(\frac{\sqrt{x}-1}{\sqrt{x}}>-1\)\(\Leftrightarrow\sqrt{x}-1>-\sqrt{x}\)\(\Leftrightarrow2\sqrt{x}>1\)
\(\Leftrightarrow\sqrt{x}>\frac{1}{2}\)\(\Leftrightarrow x>\frac{1}{4}\)thoả mãn \(x\ne1\)
Vậy \(A>-1\)\(\Leftrightarrow x>\frac{1}{4}\)thoả mãn \(x\ne1\)
1 Cho bt:A=\((\frac{1}{x+\sqrt{x}}+\frac{\sqrt{x}}{\sqrt{x+1}}):\frac{3}{\sqrt{x+1}}\)
Đkxđ và rút gọn
Tìm x để \(\frac{1}{\sqrt{x}}.A=1\)
1) cho Ax/x-1 + x/x+1 (x ko bằng +-1) và BX^2-x/x^2-1 (x ko bằng +-1)a)rút gọn A và tính A khi x2b)Rút gọn B và tìm x để B2/5c)tìm x thuộc Z để (A,B)thuộc Z 2)A (2+x/2-x - 4x^2/x^2-4 - 2-x/2+x) : x^2 - 3x/2x^2 - x^3a)rút gọn biểu thức A b) tính giá trị biểu thức A khi /x-5/2c)tìm x để A03)B x+2/x+3 - 5/x^2+x-6 - 1/2-xa)rút gọn biểu thức B b)tìm x để B3/2 c) tìm giá trị nguyên của x để B có giả trị nguyên4)C (2x/2x^2-5x+3 - 5/2x-3) : (3+2/1-x)a)rút gọn biểu thức C b) tìm giá trị nguyên...
Đọc tiếp
1) cho A=x/x-1 + x/x+1 (x ko bằng +-1) và B=X^2-x/x^2-1 (x ko bằng +-1)
a)rút gọn A và tính A khi x=2
b)Rút gọn B và tìm x để B=2/5
c)tìm x thuộc Z để (A,B)thuộc Z
2)A =(2+x/2-x - 4x^2/x^2-4 - 2-x/2+x) : x^2 - 3x/2x^2 - x^3
a)rút gọn biểu thức A b) tính giá trị biểu thức A khi /x-5/=2
c)tìm x để A>0
3)B= x+2/x+3 - 5/x^2+x-6 - 1/2-x
a)rút gọn biểu thức B b)tìm x để B=3/2 c) tìm giá trị nguyên của x để B có giả trị nguyên
4)C= (2x/2x^2-5x+3 - 5/2x-3) : (3+2/1-x)
a)rút gọn biểu thức C b) tìm giá trị nguyên của biểu thức C biết :/2x-1/=3
c)tìm x để B >1 d) tìm giá trị nhỏ nhất của biểu thức C
5)D=(1 + x/x^2+1) : (1/x-1 - 2x/x^3+x-x^2-1)
a)rút gọn biểu thức D
b)tìm giá trị của x sao cho D<1
c)tìm giá trị nguyên của x để B có giá trị nguyên
bạn viết thế này khó nhìn quá
nhìn hơi đau mắt nhá bạn hoa mắt quá
bài 1:rút gọn biểu thức
a, (a+b)\(^3\)-(a-b)\(^3\)-6a\(^2\)b
b, (x+2)\(^3\)-(x+2)\(^3\)-2x(x\(^2\)+12)
c, (x+1)\(^3\)-(x+1)\(^3\)+6(x+1)(x-1)
làm giúp mik vs ạ
1 Cho bt:A=\((\frac{1}{x+\sqrt{x}}+\frac{\sqrt{x}}{\sqrt{x}+1}):\frac{3}{\sqrt{x}+1}\)
Đkxđ và rút gọn
A = \(\frac{1+x}{x+\sqrt{x}}.\frac{\sqrt{x}+1}{3}\)=\(\frac{1+x}{3\sqrt{x}}\)
ĐKXĐ : x > 0
Đúng 0
Bình luận (0)
bài 1: rút gọn bthuca.dfrac{a+sqrt{a}}{sqrt{a}} b.dfrac{sqrt{left(x-3right)^2}}{3-x}b2: rút gọna.dfrac{sqrt{9x^2-6x+1}}{9x^2-1} b.4-x-sqrt{4-4x+x^2} c.sqrt{4x^2-4xtext{x^2 +2*x-3 0}}-sqrt{4x^2+4x+1}
Đọc tiếp
bài 1: rút gọn bthuc
a.\(\dfrac{a+\sqrt{a}}{\sqrt{a}}\) b.\(\dfrac{\sqrt{\left(x-3\right)^2}}{3-x}\)
b2: rút gọn
a.\(\dfrac{\sqrt{9x^2-6x+1}}{9x^2-1}\) b.4-x-\(\sqrt{4-4x+x^2}\) c.\(\sqrt{4x^2-4x\text{x^2 +2*x-3 >0}}-\sqrt{4x^2+4x+1}\)
Bài 1:
a) \(\dfrac{a+\sqrt{a}}{\sqrt{a}}=\sqrt{a}+1\)
b) \(\dfrac{\sqrt{\left(x-3\right)^2}}{3-x}=\dfrac{\left|x-3\right|}{3-x}=\pm1\)
Bài 2:
a) \(\dfrac{\sqrt{9x^2-6x+1}}{9x^2-1}=\dfrac{\left|3x-1\right|}{\left(3x-1\right)\left(3x+1\right)}=\pm\dfrac{1}{3x+1}\)
b) \(4-x-\sqrt{x^2-4x+4}=4-x-\left|x-2\right|=\left[{}\begin{matrix}6-2x\left(x\ge2\right)\\2\left(x< 2\right)\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Rút gọn : (x cộng 1)^3 cộng (x-1)^3 cộng x^3 -3x(x cộng 1)(x-1)
(a cộng b cộng c )^2 cộng (a cộng b - c)^2 - 2(a cộng b)^2