ho tam giác ABC kẻ AH vuông góc BC biết AB=15 cm AH= 12 HC= 16 cm .Tính độ dài các cạnh BH BC AC
NK
Những câu hỏi liên quan
cho tam giác ABC có góc BAC>90 độ . Kẻ AH vuông góc BC tại H. Biết AB=15 cm, AC=41 cm, BH=12 cm . Tính độ dài cạnh HC
Áp dụng định lý Pi-ta-go vào tam giác vuông ABH vuông tại H ta có:
AB2= BH2 + AH2
<=> 152= 122+ AH2
<=> AH2= 152- 122= 225- 144= 81
<=> AH= 9 (cm)
Tương tự ta có : Áp dụng định lý Pi-ta-go vào tam giác vuông ACH vuông tại H .
AC2= AH2+ HC2
<=> 412= 92+ HC2
<=> HC2= 412- 92= 1681- 81= 1600
<=>HC= 40 (cm)
Đúng 1
Bình luận (0)
Cho tam giác ABC có B A C ^ > 90 ° . Kẻ AH vuông góc với BC tại H. Biết AB = 15 cm; AC = 41 cm, BH = 12 cm. Tính độ dài cạnh HC.
Cho tam giác ABC vuông tại A có AC 20 cm. Kẻ AH vuông góc với BC. Biết BH 9cm, HC 16 cm. Tính độ dài cạnh AB, AH? A.
A
H
12
c
m
;
A
B
15
c
m
B.
A
H
10
c
m
;
A
B
15
c
m
C.
A
H
15
c
m
;
A...
Đọc tiếp
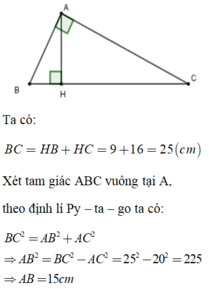
Cho tam giác ABC vuông tại A có AC = 20 cm. Kẻ AH vuông góc với BC. Biết BH = 9cm, HC = 16 cm. Tính độ dài cạnh AB, AH?
A. A H = 12 c m ; A B = 15 c m
B. A H = 10 c m ; A B = 15 c m
C. A H = 15 c m ; A B = 12 c m
D. A H = 12 c m ; A B = 13 c m
Cho tam giác ABC. Kẻ AH vuông góc với BC . Cho biết AB = 13 cm, AH = 12 cm, HC = 16 cm. Tính đọ dài các cạnh AC, BC
Tam giác AHC vuông tại H nên : AC^2 = AH^2 + CH^2 = 12^2 + 16^2 = 400
=> AC = 20 (cm)
Tam giác AHB vuông tại H nên : AB^2 = AH^2 + BH^2
=> BH^2 = AB^2 - AH^2 = 13^2 - 12^2 = 25
=> BH = 5 (cm)
=> BC = BH + HC = 5 + 16 = 21 (cm)
Tk mk nha
Đúng 0
Bình luận (0)
bài này ta sử dụng định lí Pytago là được mà
Đúng 0
Bình luận (0)
Cho tam giác ABC, kẻ AH vuông govs BC . Biết AB=5 cm; BH = 3 cm; BC= 10 cm( hình vẽ)
a, Biết góc B= 30 độ. Tính góc HAC?
b, Tính độ dài các cạnh AH, HC, AC.
Cho tam giác ABC nhọn. Kẻ AH vuông góc với BC tại H. Biết rằng AB=13 cm, AH=12 cm,HC=16 cm.Tính độ dài cấc cạnh AC, BC.
Áp dụng định lí Pytago vào ΔAHC vuông tại H, ta được:
\(AC^2=AH^2+HC^2\)
\(\Leftrightarrow AC^2=12^2+16^2=400\)
\(\Leftrightarrow AC=\sqrt{400}=20cm\)
Áp dụng định lí Pytago vào ΔABH vuông tại H, ta được:
\(AB^2=AH^2+BH^2\)
\(\Leftrightarrow BH^2=AB^2-AH^2=13^2-12^2=25\)
\(\Leftrightarrow BH=\sqrt{25}=5cm\)
Ta có: BH+CH=BC(H nằm giữa B và C)
\(\Leftrightarrow BC=5+16=21\left(cm\right)\)
Vậy: AB=20cm; BC=21cm
Đúng 2
Bình luận (1)
Cho tam giác nhọn ABC. Kẻ AH vuông góc với BC (\(H\in BC\)). Cho biết AB = 12 cm, AH = 12 cm, HC = 16 cm. Tính các độ dài AC, BC ?
Ta có:
AC2= AH2+HC2=122+162=144+156=400.
=> AC=20(cm )
BH2=AB2-AH2=132-122
=169 - 144 = 25 => BH=5(cm)
Do đó BC=BH+HC=5+16=21(cm)
Đúng 0
Bình luận (0)
Ta có:
AC2= AH2+HC2=122+162=144+156=400.
=> AC=20(cm )
BH2=AB2-AH2=132-122
=169 - 144 = 25 => BH=5(cm)
Do đó BC=BH+HC=5+16=21(cm)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Bài 1 Cho tam giác ABC vuông tại A có đường cao AH .biết BH = 9 cm ,HC = 16 cm .tính AH; AC ;số đo góc ABC (số đo góc làm tròn đến độ)
bài 2 Cho tam giác ABC vuông tại A , đường cao AH. biết AB = 3 cm ,AC = 4 cm. Tính độ dài các cạnh BC, AH và số đo góc ACB (làm tròn đến độ)
Bài 1:
AH=12cm
AC=20cm
\(\widehat{ABC}=37^0\)
Đúng 0
Bình luận (0)
cho tam giác ABC kẻ AH vuông góc BC
biết AB = 5 cm , BH = 3 cm , BC = 10 cm
a) biết C = 30 độ tính HAC = ?
b) tính độ dài các cạnh AH , HC , AC