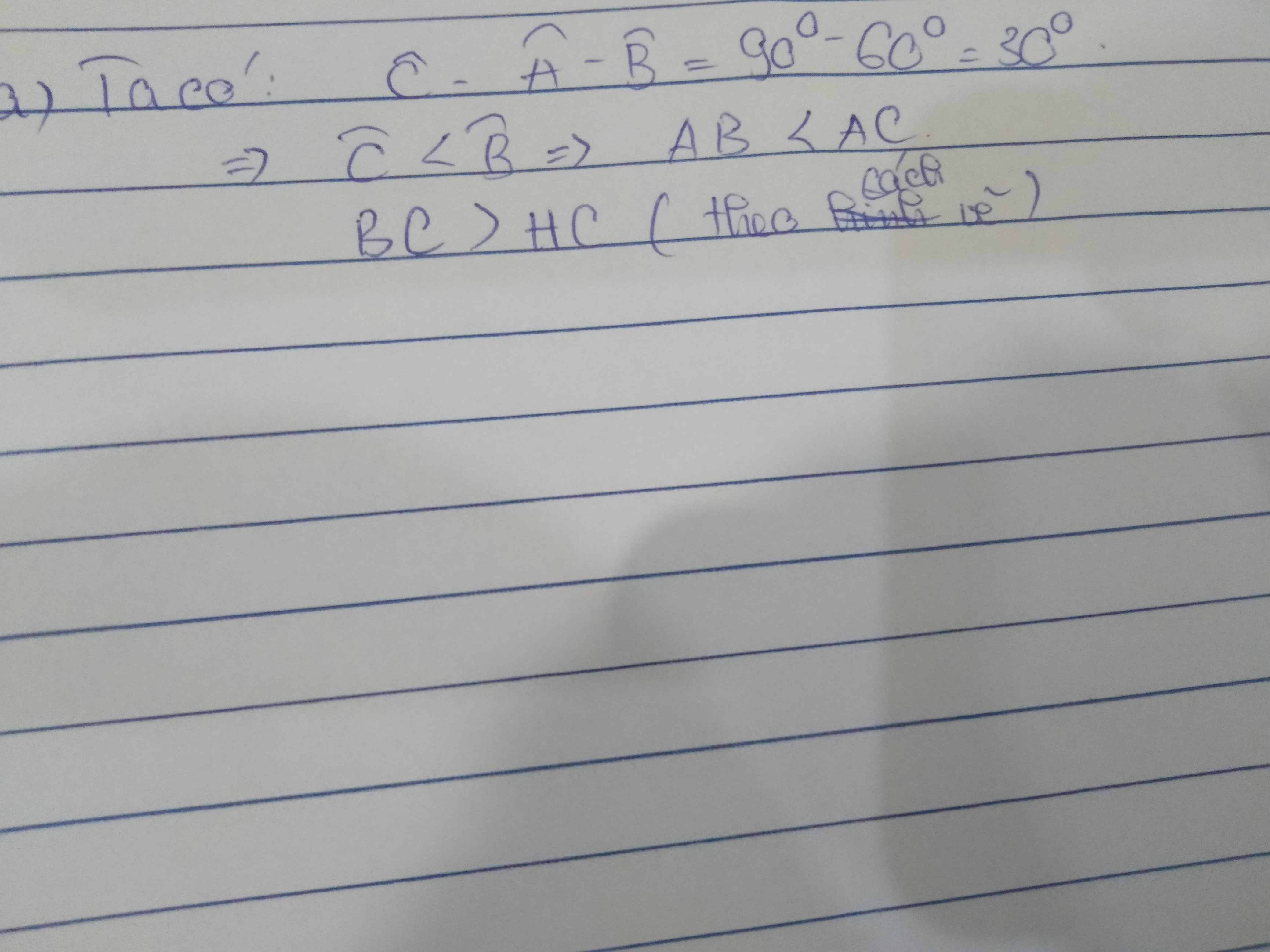Cho tam giác ABC có AH vuông góc BC và AB=HC. Hãy so sánh độ lớn của góc B và góc C
HL
Những câu hỏi liên quan
Cho tam giác ABC có góc A lớn hơn góc B, góc C lớn hơn góc B, kẻ AH vuông góc với BC, so sánh độ dài HB và HC.
Xem thêm câu trả lời
Cho tam giác ABC có góc C lớn hơn góc B kẻ AH vuông góc với BC so sánh các độ dài HB và HC
Cho tam giác ABC có AB>AC. Vẽ AH vuông tại BC ( H thuộc BC) A/so sánh góc B và góc C B/so sánh các đọan thẳng HB và HC
a)Xét t/giác ABC có AB>AC
⇒ ACB>ABC(quan hệ giữa góc và cạnh đối diện)
b) Ta có: AB > AC (gt)
⇒ HB > HC (quan hệ giữa hình xiên và đường chiếu của chúng)
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A góc B=60 độ,Vẽ AH vuông góc với BC,(H thuộc BC)
a,So sánh AB và AC;BC và HC
CHO TAM GIÁC ABC VUÔNG TẠI A CÓ GÓC C=30 . KẺ AH VUÔNG GÓC BC. TRÊN ĐOẠN THẲNG HC LẤY D SAO CHO HD=HB. E LÀ CHÂN ĐƯỜNG VUÔNG GÓC KẺ TỪ C ĐẾN AD
. CHỨNG MINH
A, , AB=AD
B, TAM GIÁC ABD ĐỀU
C, SO SÁNH AH VÀ CE
D, BIẾT AB=5CM. TÍNH ĐỘ DÀI AH VÀ BC
a: Xét ΔABD có
AH là đường cao
AH là đường trung tuyến
Do đó: ΔABD cân tại A
=>AB=AD
b: Ta có: ΔABC vuông tại A
=>\(\widehat{ABC}+\widehat{ACB}=90^0\)
=>\(\widehat{ABC}+30^0=90^0\)
=>\(\widehat{ABC}=60^0\)
Xét ΔABD cân tại A có \(\widehat{ABD}=60^0\)
nên ΔABD đều
c: Ta có: ΔABD đều
=>\(\widehat{BAD}=60^0\)
Ta có: \(\widehat{BAD}+\widehat{CAD}=\widehat{BAC}\)
=>\(\widehat{CAD}=90^0-60^0=30^0\)
Xét ΔDAC có \(\widehat{DAC}=\widehat{DCA}\left(=30^0\right)\)
nên ΔDAC cân tại D
=>DA=DC
Xét ΔDHA vuông tại H và ΔDEC vuông tại E có
DA=DC
\(\widehat{ADH}=\widehat{CDE}\)(hai góc đối đỉnh)
Do đó: ΔDHA=ΔDEC
=>AH=EC
d: Xét ΔABC vuông tại A có \(sinC=\dfrac{AB}{BC}\)
=>\(\dfrac{5}{BC}=sin30=\dfrac{1}{2}\)
=>\(BC=5\cdot2=10\left(cm\right)\)
Xét ΔAHB vuông tại H có \(sinB=\dfrac{AH}{AB}\)
=>\(\dfrac{AH}{5}=sin60=\dfrac{\sqrt{3}}{2}\)
=>\(AH=\dfrac{5\sqrt{3}}{2}\left(cm\right)\)
Đúng 0
Bình luận (0)
Cho tam giác ABC có AC>AB, góc ABC > góc ACB. Vẽ AH vuông góc BC ( H thuộc BC). Cho HC>HB.
a. Lấy điểm E trên đoạn thẳng AH. So sánh độ dài đoạn BE và BA
b. So sánh độ dài đoạn CE bà CA
c. So sánh độ dài đoạn EB và EC
a: Ta có: ΔBEH vuông tại H
nên \(\widehat{BEH}< 90^0\)
=>\(\widehat{BEA}>90^0\)
=>BA>BE
b: Ta có: ΔEHC vuông tại H
nên \(\widehat{HEC}< 90^0\)
=>\(\widehat{AEC}>90^0\)
hay CA>CE
c: Xét ΔEBC có HB<HC
mà HB là hình chiếu của EB trên BC
và HC là hình chiếu của EC trên BC
nên EB<EC
Đúng 2
Bình luận (0)
2.cho tam giác ABC có AB=AC=5CM, BC=8cm . Kẻ AH vuông góc với BC ( H thuộc BC ) a) chứng minh HB=HC và góc BAH = góc CAH. b) tính độ dài đoạn thẳng AH . c) kẻ HD vuông góc với AB tại D , kẻ HE vuông góc với AC tại E . chứng minh rằng tam giác HDE là tam giác cân
so sánh hd và hc
Cho tam giác ABC cân có AB=AC=5cm, BC= 8cm.Kẻ AH vuông góc với BC ( H thuộc BC).
a, Chứng minh HB=HC
b, Tính độ dài AH.
c, Kẻ HD vuông góc với AB(D thuộc AB), kẻ HE vuông góc với AC ( E thuộc AC).Chứng
minh tam giác HDE cân.
d, So sánh HD và HC.
Xét tam giác ABH và tam giác ACH
AB=AC(GT)
^AHB=^AHC=90o
^ABH=^ACH ( TAM GIÁC ABC CÂN TẠI A)
=> tam giác ABH = tam giác ACH
=> HB=HC ( 2c tứ)
có HB+HC=BC
mà BC=8 cm
HB=HC
=> HB=HC=4cm
Xét tam giác ABH : ^H=90o
=> AB2+AH2+BH2(đ/lý pythagoras)
thay số ta có :
52=AH2+42
25-16=AH2
9=AH2
3=AH
c)Xét tam giác BDH và tam giác ECH
^BDH= ^ HEC =90o
BH=CH
^DBH=^ECH ( TAM GIÁC ABC CÂN TẠI A)
=> tam giác BDH = tam giác ECH
=> DH=EH
=> HDE CÂN TẠI H (Đ/N)
d) qua tia đối của DH ; kẻ HK sao cho HK= DH
CÓ : tam giác HCK có cạnh HK là cạnh lớn nhất ( cạnh huyền) => HK > HC
mà HD=HK
=> HD>HC
Cho tam giác ABC có góc B=60 độ, AB=7 cm, BC=15 cm. Vẽ AH vuông góc với BC( H thuộc BC). Lấy điểm M trên HC sao cho HM=MB.CM:a. So sánh góc BAC và ACB
b,tam giác ABM đều
c, tam giác ABC có phải tam giác vuông ko? Vì sao?